在学习数学建模的过程中,最核心的问题就是从题目当中抽象出变量与关系。这是非常重要的一点。但在我指导数学建模竞赛的过程中,这一点往往也成为了学生们的痛点、难点。尤其是在美国COMAP公司举办的一些比赛(HIMCM, IMMC, MCM/ICM)当中问题变得更加隐晦,学生往往难以从题目当中发现问题所蕴含的一些数学量、数学关系,甚至不知道这个问题究竟是一个什么问题。于是,学生根本不知道用什么数学理论与工具,解题也就自然成为了空中楼阁。
所以,这一讲我们的重点就是探讨:如何从问题的背景当中理解变量与关系。
从小学数学题开始回忆
我们回忆一下小学的时候数学老师是怎么教导我们解应用题的。在小学五年级老师给大家讲述使用一元一次方程解应用题的时候,老师会教导大家:哦,要找到当中的一些量。比如路程问题,我就要抓:速度,路程,时间;比如利润问题,我就要抓:收入,支出,售卖件数,单价等;比如工程问题,要抓:不同工人的工作效率,工作时间,工作量……这是解决数学应用题的第一步。在这些量当中,有已知的,也有未知的,我们把未知量设为x就可以进行下一步。
下一步怎么办呢?老师会告诉大家:抓关系。抓什么关系?一些简单的关系就比如:路程=时间\(\times\)速度,利润=收入-成本,收入=单价\(\times\)商品数……,这些就是解应用题的关系。在问题当中可能仅靠关系还不够,我们还会涉及到一些约束。比如说,在行程问题里面有相向而行和同向而行,那么“谁与谁?怎么相遇?”就成为了一种约束。还有的一些约束比如说,商品数只会是整数而非小数,这是一个隐藏的整数约束。如果在求解过程中求出来是小数那么需要立即检查是不是哪里出了问题。这是我们小时候解决应用题的步骤。
好,通过这么一个片段来回忆,相信大家已经猜到我想表达什么了。其实自始至终,我们解决的思路一直没有变,都是抓量、找关系、看约束这么三个过程。这些重要的字词句,在问题描述当中是我们需要关注的重点,如果同学们想有针对性训练可以用笔勾画出来。
注:我其实主要搞的是数据挖掘和人工智能方面的工作,在人工智能的分支自然语言处理里面,像类似的核心概念在自然语言当中我们也可以叫它命名实体。从自然语言文字当中识别出命名实体的工作又叫命名实体识别。
如何从问题中识别量
在数学建模问题当中识别量与关系是最基础的一项工作。后面的几节我会以向量与几何问题、代数与不等式问题、函数与微分问题、概率与统计问题、图论等多个类型的问题展开具体探讨。这一节是本章第一节,所以我们仅以一个宏观视角进行针对性训练。我们只讨论如何看到量与关系,而不去具体解它。
先看一个比较简单的例子吧,这是我以前上课的时候经常给同学们讲到的。
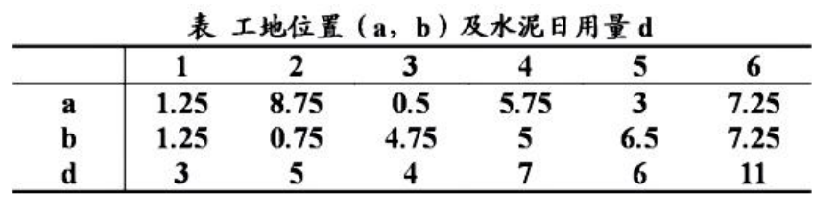
例1. 某公司有6个建筑工地要开工,每个工地的位置(用平面坐标系a,b表示,距离单位:千米)及水泥日用量d(吨)由下表给出。规划设立两个料场位于A,B,日储量各为20吨。假设从料场到工地之间均有直线道路相连,试确定料场的位置,并制定每天的供应计划,即从A,B两料场分别向各工地运送多少吨水泥,使总的吨千米数最小。
这个案例其实相对来讲没那么复杂,大家可以思考一下。
那么在这个问题当中我们应该有哪些量、哪些关系呢?首先,题目当中说到:“6个建筑工地要开工”,那首先这个“6个”就是一个条件了。“工地的位置和水泥日用量”给出,位置有横坐标、纵坐标,加上水泥日用量,我们就有3$\times$6=18个量。这18个都是常量,都在表里面给的明明白白。而“两个料场AB”,它们的位置是待求的,所以二二得四有四个未知量;日储量各为20吨,这两个料场的储量也是已知量。现在还要求解的是:“从AB两料场分别向各工地运送多少吨水泥”,那么两个料场各自向6个工地运输也就产生了12个未知量。最后“总的吨千米数”又是一个未知量,并且这个量与前面是存在明确的换算关系的。
据此,我们可以列举一下里面的常量与变量:
- 已知常量:六个工地的横坐标、纵坐标、水泥日用量,两个料场的储量
- 未知变量:两个料场的横坐标、纵坐标、12条道路上的水泥运载量,总的吨千米数
这样,我们就算完成了第一步工作。大家有一些体会了吗?
我们再来看一个例子,这个例子是2023年全国大学生数学建模竞赛的B题。我们只看第一问。
例2. 2023年全国大学生数学建模竞赛B题
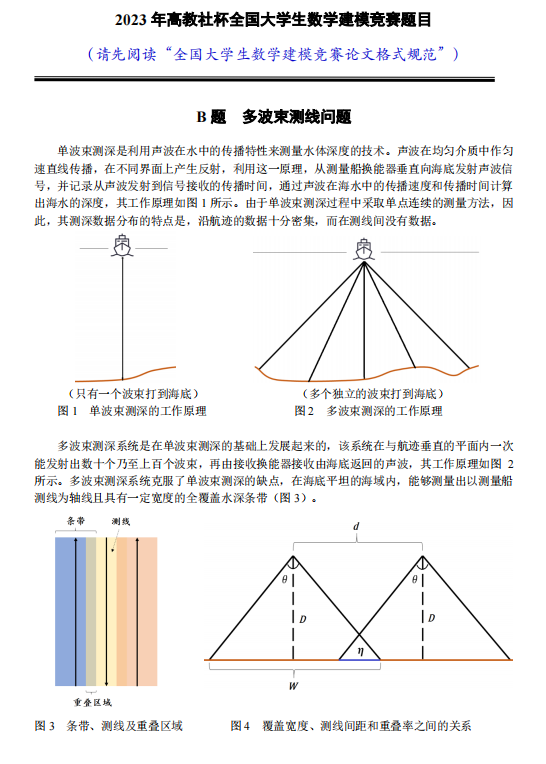
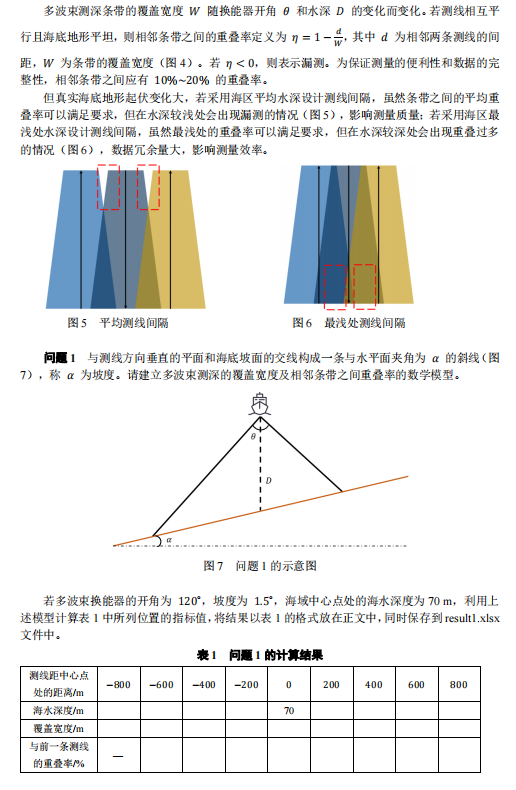
这个问题看起来很长对吧,这是一个正儿八经的比赛题目。问题当中出现的量其实非常明确,题目里面都给我们标记好了。第一是探测船竖直向下到海底面的深度D,第二是探测船的张角\(\theta\),探测船从图4里面看是垂直纸面的航行方向,但可以左右平移一个距离d。探测船与海底面的波束探测区域记作W,也就是探测船最左边一条波束和最右边一条波束之间的距离。相邻两个条带之间的覆盖率叫做\(\eta\),这里题干还贴心给出了计算方法。海底面的斜率是1.5°,又是一个已知量。这样我们就总结了里面所有的量。现在,大家自行按照上面的方式归纳哪些是变量,哪些是常量,哪些是已知量,哪些是未知量。我想,大家只要能想到这些,第一问自己是有办法做的。
最后看一个比较虚的例子。这道题是2022年美国高中生数学建模竞赛的A题。大家不至于不敢做高中生的题目吧(笑)。
例3. 2022年美国中学生数学建模竞赛A题
蜜蜂种群增长,这个题典型的COMAP美式风格。你甚至第一眼都不知道他到底在问什么,让你建模型,建个怎么样的模型?里面应该包含点什么?鬼晓得。那我们就要想了,这个题,种群增长,它其实不就可以用一个种群增长的微分方程模型吗?好,既然如此我们回忆:在以往一些教材(例如姜启源、韩中庚甚至我的网课《数学建模导论》)里面都讲到过种群增长,他可以是一个Malthus的,也可以是一个Logistic的,核心奥义无非就是:增长率、初始种群数量、最大种群数量的限制,把握住这三个量的关系,自己去查一下实际的数值,还怕没东西写吗?非常好,这就是这道问题的Baseline。在此基础上,有人想引入时滞项,有人想种群竞争,还有人想绕开这个把蜜蜂的生命周期引入进来用微分方程组解,都可以,但都是在此基础上魔改。
我们不怕题目里面变量多,就怕他不给。但是哪怕不给,我们还可以从知识出发,我们还可以非常创造性、跨越性的迁移一些知识过来。这一点,我们在后面的内容里面会讲到。
如何从问题中找到关系
识别量只是第一步,关系才是最核心的模型。数学当中的关系包括等量关系、不等关系、函数关系、概率统计关系等等。有这么多关系,我怎么知道该要哪个不该要哪个呢?其实核心在于关键词,以及我们对关键词的解读。当然,同一句话,有些人可能会认为这句话说的是等量关系,另一些人可能就会认为这句话说的是不等关系,我认为只要说的有足够的理由都是可以接受的。尤其是在规划问题当中,有些条件写成等式和写成不等式对结果其实并没有什么影响。
我们还是回顾到例1上来。怎么描述的一些变量之间关系呢?核心首先,AB的日储量都是20吨,A送到6个工地的运载量之和就不能超过20吨,B到6个工地的运载量之和也不能超过20吨。这就是两个不等式。那反过来,6个工地,对于每个工地它都会有从A送来的水泥和从B送来的水泥,这两部分水泥的和不能少于它的水泥日用量,这就又是6个不等式。(注:这里有同学可能认为写成等式也可以,这个地方我验算过确实是可以的)。最后吨千米数与AB坐标、12条边的运载量和6个工地坐标之间的关系可以用距离公式加权求和得到,是一个多元函数的函数关系。最后的问题目标是需要我们求解总的吨千米数的最小值,是一个有约束条件下多元函数的最优化问题,通过设量、列关系,把上述分析转化为数学语言就可以得到:
这里的x是一个16维的向量,前四维表示两个料场的坐标,后面12个分别表示料场1到六个工地的运输量和料场2到六个工地的运输量。运输量之间需要满足限制。首先,料场1到六个工地的运输量之和与料场2到六个工地的运输量之和都不能超过20吨,这是存量的限制;其次,每个工地从两个料场获取的运输量之和得等于自己的一个需求量。这里其实如果把每个工地的限制看作一个大于等于也是说得通的,但我们这里为了求解方便把这一部分看作等式约束也是没问题的。
再看看例2我们怎么解。两个三角形会发生重合。事实上这个d是船的轴心左右偏移,而不是沿着探测船的方向前后偏移,首先理解了这一点才是问题解决的关键。已知开角120度,坡度为1.5度,D=70,求覆盖宽度,这个问题本质上就是一个已知三角形角度和角平分线长度求对边的几何问题。考的是初中几何的知识。
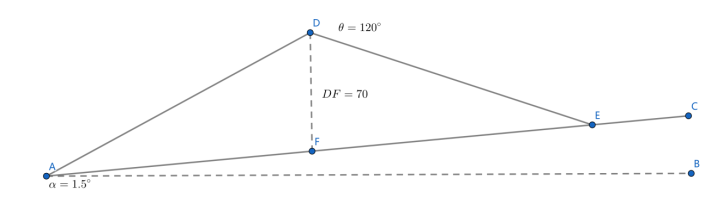
在这个图中,很显然,角DAB+角ADF=90度,角CAB=1.5度,角ADF为开角的一半也就是60度,所以角DAF为28.5度,也就知道了DEA为31.5度。已知DF长度为70,还知道对角,可以使用正弦定理:
所以带宽的长度也就是AF+EF。
考虑两条测线的情况,如图:
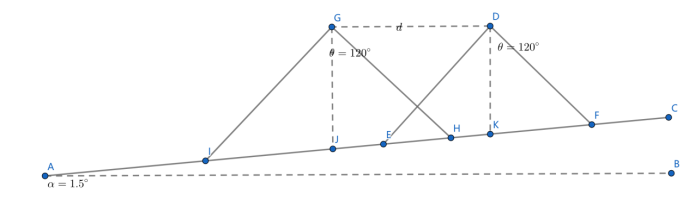
很显然,重叠部分的覆盖宽度W=EH。那么EH的长度很显然,有关系:EH=JH-EK-JK, 由于GD//AB,三角形GIH和三角形DEF的张角都为120度,可以推出这两个三角形相似。根据前面我们通过正弦定理得到的推论,有:
这样,问题就可以迎刃而解。
大家下去以后还可以做一些针对性的训练,看如何从自然语言描述的问题当中抽象出数学语言描述。使用数学语言描述问题,实际上就是识别量和构建关系的过程,这是数学建模的基础性工作,也是做好后面所有工作的大前提。