CF1753 题解
A
首先我们发现,我们可以将序列一部分取反,将1变-1,-1变1的操作每次将总和增加2,所以如果初始和的绝对值为奇数则无解。
我们发现,一段区间可以拆成若干个长度为2和1的小区间(+-+-+-+-....)变成(+- +- +- ...)。我们假设初始都是长度为1的小区间,这时答案等于所有数的总和。我们将两个1区间合并成一个2区间,就会将第二个数取反,所以我们导出一种方案:\(dp\)。
假设1的数量多于-1的数量(0不管)。我们从前向后扫描,如果\(a_i\)为1,就将\(a_i\)与\(a_{i - 1}\)放在一起,所以\(dp_i = dp_{i - 2} + 2\),如果\(sum - dp_i = 0\),后面的数就不变,记\(i\)的转移点,然后输出即可。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int n,a[N],f[N],from[N],l[N],r[N],tot = 0;
int main()
{
int T;
cin>>T;
while(T--)
{
tot = 0;
int sum = 0;
cin>>n;
for(int i = 1;i <= n;i++) cin>>a[i],sum += a[i];
if(sum & 1)
{
cout<<-1<<endl;
continue;
}
if(sum == 0)
{
cout<<n<<endl;
for(int i = 1;i <= n;i++) cout<<i<<" "<<i<<endl;
continue;
}
else if(sum < 0)
{
f[0] = 0;f[1] = 0;
for(int i = 2;i <= n;i++)
{
if(sum + f[i - 2] < 0 && a[i] == -1) f[i] = f[i - 2] + 2,from[i] = i - 2;
else f[i] = f[i - 1],from[i] = i - 1;
}
if(f[n] + sum < 0)
{
cout<<-1<<endl;
continue;
}
for(int i = n;i >= 1;i = from[i])
{
++tot;
l[tot] = from[i] + 1;
r[tot] = i;
}
cout<<tot<<endl;
for(int i = tot;i >= 1;i--) cout<<l[i]<<" "<<r[i]<<endl;
}
else
{
f[0] = 0;f[1] = 0;
for(int i = 2;i <= n;i++)
{
if(sum + f[i - 2] > 0 && a[i] == 1) f[i] = f[i - 2] - 2,from[i] = i - 2;
else f[i] = f[i - 1],from[i] = i - 1;
}
if(f[n] + sum < 0)
{
cout<<-1<<endl;
continue;
}
for(int i = n;i >= 1;i = from[i])
{
++tot;
l[tot] = from[i] + 1;
r[tot] = i;
}
cout<<tot<<endl;
for(int i = tot;i >= 1;i--) cout<<l[i]<<" "<<r[i]<<endl;
}
}
return 0;
}
B
本来,这个题很麻烦。
但是\(x \leq 5e5\)。
我们发现可能有重复数字,根据柿子\((i + 1)i! = (i + 1)!\),我们可以记一个桶,从小到大扫,向前进位,最后得到的就是最简形式。
这是我们发现,\(x\)以下的桶如果还有数字的话,小到无法凑成一个\(x!\),那么这些就是原数模\(x!\)的余数,不能整除,否则可以。
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n,a[N],t[N],x;
int main()
{
cin>>n>>x;
for(int i = 1;i <= n;i++) cin>>a[i],t[a[i]]++;
int e = 0;
for(int i = 1;i <= x - 1;i++)
if(t[i])
{
if(t[i] % (i + 1) == 0) t[i + 1] += t[i] / (i + 1),t[i] = 0;
else e = 1;
}
if(e) cout<<"No";
else cout<<"Yes";
return 0;
}
C
考虑到排序后一定0在前面,1在后面,一个操作,假设1有\(cnt_1\)个,那么这个操作只有一个1和后面的\(n - cnt_1 + 1\)位置中的0交换后,在“正确位置”的1又多了一个,否则和原来等价。
假设\(dp_i\)为有\(i\)个1回到正确位置的期望步数,则有:
化简得:
有\(dp_{cnt_1} = 0\),递推即可。
#include<bits/stdc++.h>
using namespace std;
const int MOD = 998244353,N = 2e5 + 5;
typedef long long ll;
ll dp[N],n,cnt1 = 0,a[N],now = 0,c,inv;
inline ll ksm(ll base,ll pts)
{
ll ret = 1;
for(;pts > 0;pts >>= 1,base = base * base % MOD)
if(pts & 1)
ret = ret * base % MOD;
return ret;
}
int main()
{
int T;
cin>>T;
while(T--)
{
cin>>n;cnt1 = 0;now = 0;
c = n * (n - 1) / 2 % MOD;
inv = ksm(c,MOD - 2);
for(int i = 1;i <= n;i++) cin>>a[i],cnt1 += (a[i] == 1);
for(int i = n - cnt1 + 1;i <= n;i++) now += (a[i] == 1);
dp[cnt1] = 0;
for(int i = cnt1 - 1;i >= now;i--)
{
ll rate = (cnt1 - i) * (cnt1 - i) % MOD * inv % MOD;
rate = ksm(rate,MOD - 2);
dp[i] = (dp[i + 1] + rate) % MOD;
}
cout<<dp[now]<<endl;
}
return 0;
}
D
可以证明一个障碍只会旋转一次,见洛谷Sword_K题解:CF1753D The Beach - Sword_K 的博客 - 洛谷博客 (luogu.com.cn)
“因为一旦出现了这种情况,这张床周围至少有 2 个空格,那么最多只需要操作这张床一次就可以把两个空格挪到一起。即不合法的答案一定不优。”
所以我们将旋转,平移看作一个空格的移动,按以下方式建边,跑多源最短路即可(dijkstra),答案就是两个相邻点距离空点距离之和。
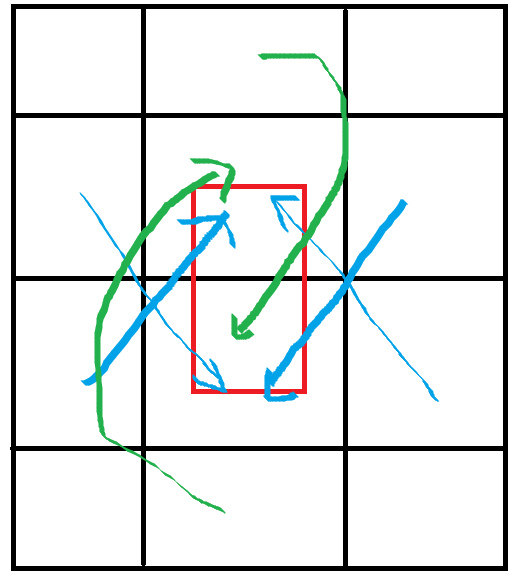
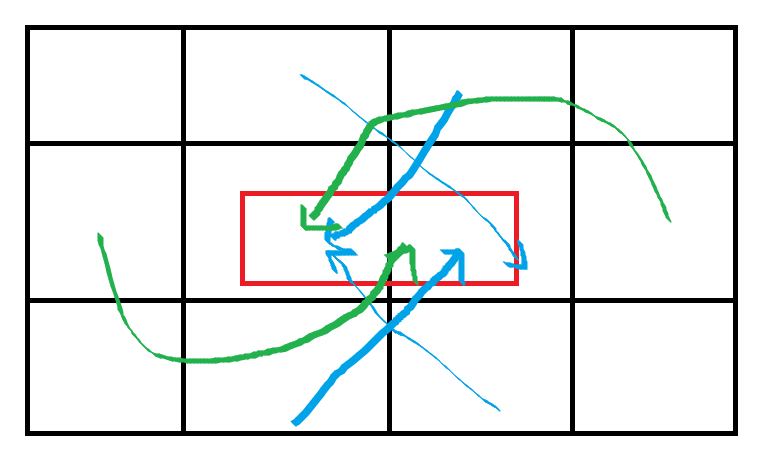
(蓝边长度为p,绿边长度为q)
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5 + 5;
typedef long long ll;
const ll inf = 0x3f3f3f3f3f3f3f3f;
vector <char> a[N];
vector <int> pos[N];
struct Edge{
int v,w,next;
}e[N * 10];
int tot = 0,n,m,P,Q,vis[N],head[N];
inline void add(int x,int y,int z)
{
++tot;
e[tot].v = y;
e[tot].w = z;
e[tot].next = head[x];
head[x] = tot;
}
priority_queue <pair<ll,int> , vector<pair<ll,int> > , greater<pair<ll,int> > > q;
ll dis[N];
inline bool ck(int x,int y)
{
if(x >= 1 && x <= n && y >= 1 && y <= m && a[x][y] != '#') return true;
return false;
}
inline void dijkstra()
{
while(!q.empty())
{
int x = q.top().second;
q.pop();
if(vis[x]) continue;
vis[x] = 1;
for(int i = head[x];i;i = e[i].next)
{
int to = e[i].v;
if(vis[to]) continue;
if(dis[to] > dis[x] + e[i].w)
{
dis[to] = dis[x] + e[i].w;
q.push(make_pair(dis[to],to));
}
}
}
}
int main()
{
cin>>n>>m>>P>>Q;
char c;
for(int i = 1;i <= n;i++)
{
a[i].push_back('a');
pos[i].push_back(0);
for(int j = 1;j <= m;j++)
{
cin>>c;
pos[i].push_back(++tot);
a[i].push_back(c);
}
}
tot = 0;
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
dis[pos[i][j]] = inf;
if(a[i][j] == '#') continue;
if(a[i][j] == '.')
{
dis[pos[i][j]] = 0;
q.push(make_pair(0,pos[i][j]));
}
if(a[i][j] == 'U')
{
if(ck(i + 1,j - 1)) add(pos[i + 1][j - 1],pos[i][j],P);
if(ck(i + 1,j + 1)) add(pos[i + 1][j + 1],pos[i][j],P);
if(ck(i + 2,j)) add(pos[i + 2][j],pos[i][j],Q);
}
if(a[i][j] == 'D')
{
if(ck(i - 1,j - 1)) add(pos[i - 1][j - 1],pos[i][j],P);
if(ck(i - 1,j + 1)) add(pos[i - 1][j + 1],pos[i][j],P);
if(ck(i - 2,j)) add(pos[i - 2][j],pos[i][j],Q);
}
if(a[i][j] == 'L')
{
if(ck(i - 1,j + 1)) add(pos[i - 1][j + 1],pos[i][j],P);
if(ck(i + 1,j + 1)) add(pos[i + 1][j + 1],pos[i][j],P);
if(ck(i,j + 2)) add(pos[i][j + 2],pos[i][j],Q);
}
if(a[i][j] == 'R')
{
if(ck(i - 1,j - 1)) add(pos[i - 1][j - 1],pos[i][j],P);
if(ck(i + 1,j - 1)) add(pos[i + 1][j - 1],pos[i][j],P);
if(ck(i,j - 2)) add(pos[i][j - 2],pos[i][j],Q);
}
}
}
dijkstra();
ll ans = inf;
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
{
if(ck(i + 1,j)) ans = min(ans,dis[pos[i + 1][j]] + dis[pos[i][j]]);
if(ck(i,j + 1)) ans = min(ans,dis[pos[i][j + 1]] + dis[pos[i][j]]);
}
cout<<(ans == inf ? -1 : ans);
return 0;
}
E
最优策略一定是加法堆前面,乘法堆后面。除去为1的乘法,我们发现乘法最多有31个。可以搜索哪些乘法提到了后面,这里要经过优化:如果对于\(i < j,a_i > a_j\),则挪\(a_i\)一定优于\(a_j\)。所以我们从前往后扫,如果遇到一个值\(a_i\),就将乘法中所有等于\(a_i\)的一起枚举,可以优化复杂度,如果所有乘法都不同,则\(13! > 2e9\),缩小到了\(2^{13}\)。
接下来处理加法,我们优先移动将\(a_i\)移动到前面时多出的贡献最大的数,将加法按照在第几个乘法后面分块,同一块内一定是值最大的贡献最大,所以块内排序,首先枚举乘法,用剩余的钱看加法,二分被选的所有加法中贡献最小的值,判断就看以当前贡献标准加入的值个数是否符合钱数条件,遍历每一个块,块内二分找出这个值,将块内选出的值和未选出的值分别做贡献加入\(sum\),将加好的\(sum\)和\(ans\)取\(max\),由于块的个数小于等于乘法操作的个数,所以时间复杂度为\(O(2^{13} \times \log^2V \times\log n),V = 2e9\),可以通过。
注意每次二分贡献最小值后,如果算出来用的操作比能用的操作略小,那么一定是被\(l - 1\)卡住了,加上挪几个贡献为\(l - 1\)的数到前排的贡献。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
vector <ll> k[100],s[100],pos[100];
ll n,m,b,p,mul[N],dt = 0,cnt = 0,tot = 0,prod = 1,use[N],ans = 1,sum = 0;
map<ll,int> mp;
inline bool cmp(int x,int y)
{
return x > y;
}
inline int ck(ll x)
{
int num = 0;
sum = prod;
ll M = prod;
for(int i = 0;i <= cnt;i++)
{
if(i && !use[i]) M /= mul[i];
if(M == prod)
{
if(s[i].size() > 0) sum += s[i][s[i].size() - 1] * M;
continue;
}
int l = 0,r = k[i].size();
while(l < r)
{
int mid = (l + r + 1) >> 1;
if((prod - M) * k[i][mid - 1] < x) r = mid - 1;
else l = mid;
}
if(l == 0)
{
if(s[i].size() > 0) sum += s[i][s[i].size() - 1] * M;
}
else
{
num += l;
sum += s[i][l - 1] * prod + (s[i][s[i].size() - 1] - s[i][l - 1]) * M;
}
}
return num;
}
inline void gv(ll X)//有X元
{
ll l = 0,r = 1e18;
X /= p;
while(l < r)
{
ll mid = (l + r) >> 1;
if(ck(mid) <= X) r = mid;
else l = mid + 1;
}
int ret = ck(l);
sum += (X - ret) * (l - 1);
ans = max(ans,sum);
}
inline void dfs(int x,int y)
{
if(m * y > b) return;
if(x == dt + 1)
{
gv(b - m * y);
return;
}
dfs(x + 1,y);
for(int i = 0;i < pos[x].size();i++)
{
use[pos[x][i]] = 1;
dfs(x + 1,y + i + 1);
}
for(int i = 0;i < pos[x].size();i++) use[pos[x][i]] = 0;
}
int main()
{
scanf("%lld%lld%lld%lld",&n,&b,&p,&m);
char c;int x;
for(int i = 1;i <= n;i++)
{
c = getchar();
while(c != '*' && c != '+') c = getchar();
scanf("%d",&x);
if(c == '*')
{
if(x == 1) continue;
++cnt;
if(mp.find(x) == mp.end()) mp[x] = ++dt;
pos[mp[x]].push_back(cnt);
mul[cnt] = x;
ans *= x;
prod *= x;
}
else
k[cnt].push_back(x),ans += x;
}
for(int i = 0;i <= cnt;i++)
{
sort(k[i].begin(),k[i].end(),greater<int>());
for(int j = 0;j < k[i].size();j++)
{
s[i].push_back(k[i][j]);
if(j) s[i][j] += s[i][j - 1];
}
}
dfs(1,0);//第几个乘法值,用了多少
printf("%lld\n",ans);
return 0;
}
F
咕。