给定一个长度为 \(n\) 的数组 \(a\),其中 \(a_i \in [1, n]\),试计算满足以下条件的 \([1, n]\) 的排列 \(p\) 的个数:
- \(\forall i \in [1, n], \sum_{1 \le j \le i} [p_j \le i] = a_i\)
\(n \le 2 \times 10^5\)。
图是拿 Excel 画得,有点丑,请见谅。
将 \((i, p_i)\) 视为二维平面上的点,则 \(a_i\) 的限制就等价于在原点到点 \((i, i)\) 的正方形内一共填了 \(a_i\) 个数字。
举个例子:
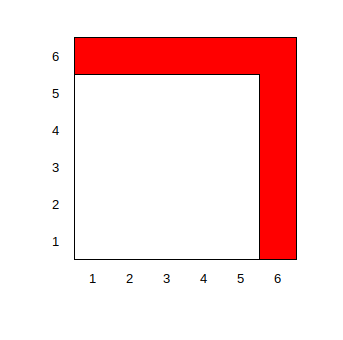
假设我们已经填完了前 \(5\) 个位置的数,现在要填 \(i = 6\) 的情况。设 \(a_5 = 3, a_6 = 5\),那也就是说我们要在红色的 L 形区域中填两个数。
而 \(p\) 是排列,且一个位置只能填一个数字,因此我们可以得到,已填数字的横坐标是互异的,其纵坐标也是互异的。那么也就是说,在这个红色的 L 形区域中,我们最多也只能填两个数字。否则就一定会出现某两个数字横坐标或者纵坐标相等的情况。因此我们得到,若设 \(a_0 = 0\) 则 \(\forall i \in [i, n], a_i - a_{i - 1} \in \{0, 1, 2\}\)。
但是是不是所有的红色格子里都能填数字呢?也不是。由于需要满足之前的限制,因此此时在横坐标 \([1, i - 1]\) 的范围里,已经有 \(a_{i - 1}\) 个纵坐标 \(\in [1, i - 1]\) 的格子被占用了。再用上边的数据举个例子:
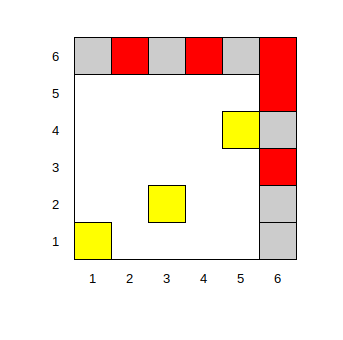
假设此时为了满足 \(a_5 = 3\) 的限制,我们在 \((1, 1), (3, 2), (5, 4)\) 这三个点上填上了数字,那么显然,此时横坐标为 \(1, 3, 5\),纵坐标为 \(1, 2, 4\) 的格子就都不可用了,剩下的位置只有 \(5\) 个是可用的了。
记 \(d_i = a_i - a_{i - 1}\),那么我们此时就可以开始分类讨论了:
- 若 \(d_i = 0\),则不需要填数字,方案数不变。
- 若 \(d_i = 1\),则需要填一个数字,方案数为 \(2(i - a_{i - 1}) - 1\)。
- 若 \(d_i = 2\),则需要填两个数字,且此时 \((i, i)\) 是不能填的,否则就只能填一个数字了,因此方案数为 \((i - a_{i - 1} - 1)^2\)。
这样就可以做到时空复杂度线性了!
无解的话,判断一下 \(d\) 的大小和 \(a_n\) 是否为 \(n\) 以及 \(a_1\) 是否 \(\le 1\) 就行了吧
- Permutation Problem Version 1909F Smallpermutation problem version 1909f permutation codeforces problem 1909i permutation codeforces problem version permutation codeforces another problem permutation another problem 1858c 题解permutation another problem 题解permutation abnormal version permutation problem 359 1909 1909d