Dijkstra算法
1.算法基本介绍
Dijkstra 算法是一个基于「贪心」、「广度优先搜索」、「动态规划」求一个图中一个点到其他所有点的最短路径的算法,时间复杂度 O(n2)。
Dijkstra算法通常是求解单源最短路中最快的算法,但它无法处理存在负权边的情况(原因在正确性证明中)。Dijkstra本质上是一种贪心算法,通过不断调整每个点的“当前距离”最终得到最优结果,其实后面要讲到的几种算法也大都是采用这种步步逼近的手段。这种不断调整的过程,维基百科上面称为“relax"。以上可能有点抽象,下面是算法的流程。
图解:
假设有下面这个图:
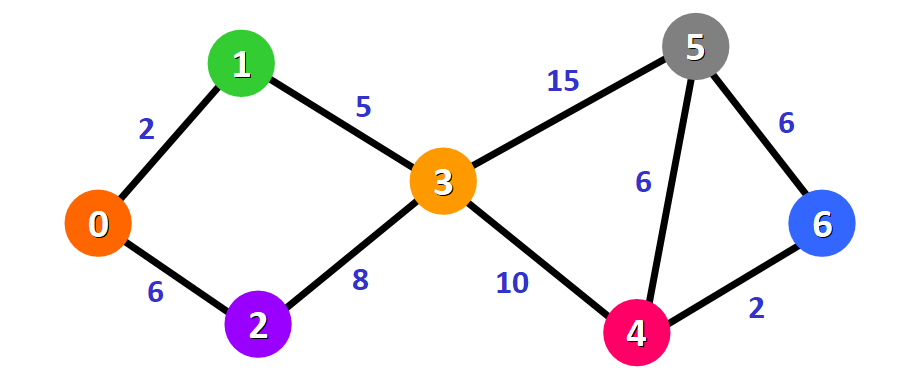
Dijkstra 算法将会寻找出图中节点 0 到所有其他节点的最短路径。
? 提示: 在这个图中,我们假定两个节点之间的权重表示它们之间的距离。
我们将会得到节点 0 到节点 1、节点 0 到节点 2、节点 0 到 节点 3……(以此类推)的最短路径。
初始的距离列表如下:
- 源节点到它自身的距离为
0。示例中的源节点定为节点0,不过你也可以选择任意其它节点作为源节点。 - 源节点到其它节点的距离还没有确定,所以先标记为无穷大。

还有一个列表用来记录哪些节点未被访问(即尚未被包含在路径中):

? 提示: 记住,当所有节点都被添加到路径中时,算法的计算过程就完成了。
我们选择了从节点 0 出发,可以直接将它标记为“已访问”,同样的,在未访问节点列表中把它划掉,并在图中给它加上红色的边框:

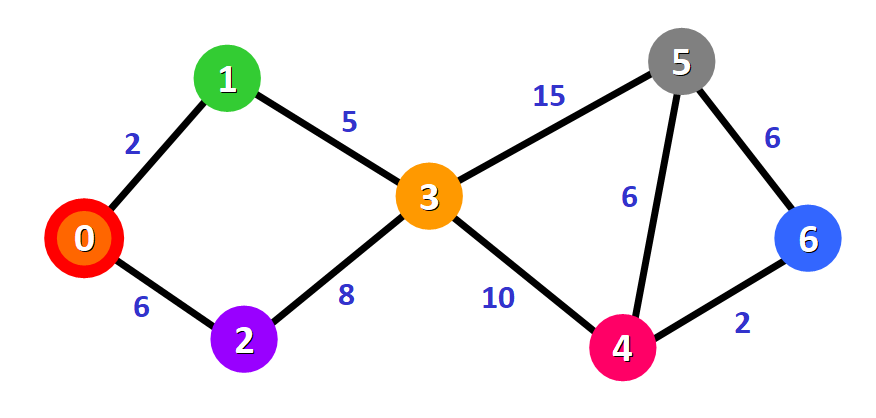
现在需要检查节点 0 到相邻节点的距离,两个相邻节点分别是节点 1 和节点 2(注意看红色的边):
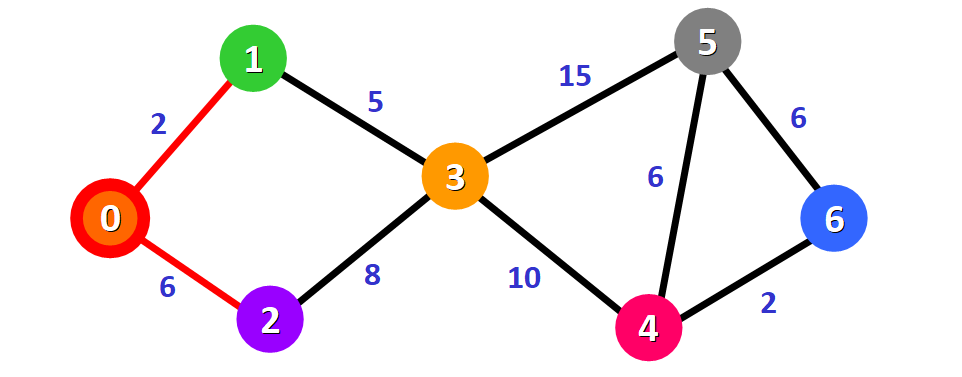
? 提示: 这并不是说立即把这两个相邻节点加入到最短路径中。在把一个节点加入到最短路径之前,需要确认是否已经寻找到了访问它的最短路径。现在只是在对可选方案做初步检查。
更新节点 0 到节点 1、节点 0 到节点 2 的距离为它们之间的边的权重,分别为 2 和 6:

更新了到相邻节点的距离之后:
- 根据已知的距离列表选择距离源节点最近的节点。
- 将它标记为“已访问”。
- 将它添加到路径中。
查看距离列表,发现节点 1 到源节点的距离是最短的(距离为 2),所以把它加入到路径中。
在图中,以红色边来表示:
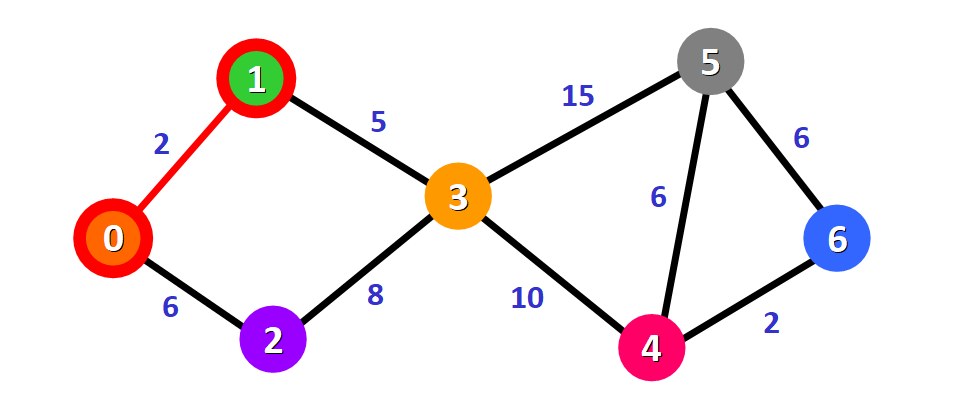
在距离列表中用红色方块标记这个节点,表明它是“已访问”的、已经寻找到了访问这个节点的最短路径:

在未访问节点列表中将它划掉:

现在分析新的相邻节点,寻找访问它们的最短路径。只需要分析已经在最短路径(标记为红色边)中的节点的相邻节点。
节点 2 和节点 3 都是最短路径包含的节点的相邻节点,因为它们分别与节点 0 和节点 1 直接相连,如下图所示。下一步将要分析这两个节点。

之前已经计算过源节点到节点 2 的距离,并记录在了列表中,所以不用更新。这次只需要更新源节点到新的相邻节点(节点 3)的距离:

这个距离是 7,来看看为什么。
为了计算源节点到另一个节点(这里指节点 3)的距离,需要把访问该节点的最短路径的所有边权重相加:
- 对于节点
3: 将构成路径0 -> 1 -> 3的所有边权重相加,得到总距离为 7(0 -> 1距离为 2,1 -> 3距离为 5)。

现在得到了到相邻节点的距离,需要选择一个节点添加到路径中。我们必须选择一个已知到源节点距离最短的未访问节点。
从距离列表中可以看出,距离为 6 的节点 2 就是我们的选择:

在图中为它加上红色边框,并将路径上的边标记为红色:

在距离列表中用红色方块把它标记为“已访问”,在“未访问”节点列表中把它划掉:


重复前面的步骤,寻找源节点到新的相邻节点节点 3 的最短路径。
可以看到,有两种可选的路径:0 -> 1 -> 3 或 0 -> 2 -> 3。一起看看我们是如何确定最短路径的。

节点 3 在之前已经有了一个距离记录(距离为 7,参阅下表),这个距离是之前步骤中由路径 0 -> 1 -> 3 的两个边权重(分别为 5 和 2)相加得到的。
不过现在有了一个新的可选路径:0 -> 2 -> 3,它途经权重分别为 6 和 8 的两条边 0 -> 2 和 2 -> 3,总距离为 14。

显然,第一个路径的距离更短(7 vs. 14),所以选择第一个路径 0 -> 1 -> 3。只有在新的路径距离更短的情况下,才会更新距离列表。
因此,使用第一种方案 0 -> 1 -> 3,将节点添加到路径中。

把这个节点标记为“已访问”,在“未访问”节点列表中把它划掉:


重复前面的过程。
检查尚未访问的相邻节点:节点 4 和节点 5,因为它们是节点 3 的相邻节点。

更新它们到源节点的距离,尝试寻找更短的路径:
- 对于节点
4: 路径是0 -> 1 -> 3 -> 4,距离为 17。 - 对于节点
5: 路径是0 -> 1 -> 3 -> 5,距离为 22。
? 提示: 注意我们只能从最短路径(红色边)上进行扩展,而不能途经未被包含在最短路径中的边(例如,不能构造经过边 2 -> 3 的路径)。
然后以此类推即可。
原文:Dijkstra's Shortest Path Algorithm - A Detailed and Visual Introduction,作者:Estefania Cassingena Navone
原题链接:Dijkstra Algorithm - Problems - Eolymp
例题1:
The directed weighted graph is given. Find the shortest path from the vertex s to the vertex f.
Input data
The first line contains three numbers n, s and f (1 ≤ n ≤ 100, 1 ≤ s, f ≤ n), where n is the number of vertices in a graph. Each of the next n lines contains n numbers - the adjacency matrix of the graph, where the number in the i-th line and j-th column corresponds to the edge from i to j: -1 means the absence of the edge between the vertices, and any non-negative number - the presence of the edge of a given weight. The main diagonal of the matrix contains always zeroes.
Output data
Print the required distance or -1 if the path between the given vertices does not exist.
Examples
Input example #1
3 1 2
0 -1 2
3 0 -1
-1 4 0
Output example #1
6
Vector版本:
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
int main()
{
int n, s, f;
cin >> n >> s >> f;
vector<vector<int>> graph(n, vector<int>(n));//定义了一个n行n列的graph向量
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> graph[i][j];//输入邻接矩阵的权
}
}
/*
dist 向量表示起点 s 到每个节点的最短距离,初始化为无穷大。
visited 向量用于标记每个节点是否被访问过,初始化为 false。
*/
vector<int> dist(n, INF);//初始化dis
vector<bool> visited(n, false);//初始化visited
dist[s-1] = 0; //s到自身的距离为0
for (int i = 0; i < n; i++)
{
int u = -1;//给出一个非法值,判断判断是否已经找到了离起点最近的未访问节点。
//如果 u 的值不是 -1,说明找到了离起点最近的未访问节点.
for (int j = 0; j < n; j++)
{
if (!visited[j] && (u == -1 || dist[j] < dist[u])) //判断当前节点 j 是否为起点 s 的第一个访问节点
{
u = j;
}
}
if (dist[u] == INF)
{
break;//如果 u 的值仍然为 -1,说明没有找到符合条件的未访问节点,此时就需要结束 Dijkstra 算法的迭代
}
visited[u] = true;
for (int v = 0; v < n; v++)
{
if (graph[u][v] != -1)//-1的时候是两点间并未相连 即没有路径可走
{
int alt = dist[u] + graph[u][v];
if (alt < dist[v])
{
dist[v] = alt;
}
}
}
}
if (dist[f-1] == INF)
{
cout << -1 << endl;
}
else
{
cout << dist[f-1] << endl;
}
/*
最后,检查 dist[f-1] 的值,如果为无穷大,则说明起点 s
无法到达终点 f,输出 -1。否则,输出起点 s
*/
return 0;
}
/*
输入:
3 1 2
0 -1 2
3 0 -1
-1 4 0
输出:
6
*/