NOIP2023模拟9联测31 总结

题目

T1 游戏

大意

博弈论，在 \(1—n\) 中 \(\phi(i)\) 小于 \(m\) 都选入集合 \(S\)。在集合 \(S\) 中选数 \(x\)，选择完后把数 \(x\) 及其的因数从 \(S\) 中删去。当不能取数时的人败。给 \(n,m\) 求先手胜还是后手胜。

\(1 \leq n \leq 100,0 \leq m \leq n\)。

比赛思路

发现一个数进入集合，那么它的所有因数也一定进入集合，将每个数向自己去除一个质因子（只减少一个指数）后的数连有向边，每个数被删掉后那么和这个点连有向边的节点也会被删除。然后后面就没想法了，但是手动模拟发现 \(Alice\)（先手）的胜率极高，于是在前前后后浪费两小时后写了 \(Alice\) 的表。

正解思路

如果有一种情况先手可以获胜，那么直接取先手。如果不可以获胜，取走 \(1\)，将几乎相同的局面留给对手，那么对手将不可以获胜。特别的，对于 \(m=0\) 的情况，后手获胜。

T2 涂鸦

大意

有 \(n*m\) 个格子，每次操作选择 \((x,y,c)\)，表示将 \((1,1)\) 到 \((x,y)\) 的矩形染成 \(c\) 颜色（\(c \in {0,1}\)），花费 \(x*y\)。每次操作在 \(n*m*2\) 种操作中随机选一。给出初始状态，目标状态，求到目标的期望代价。

比赛思路

观察了样例的解释，觉得应该和方程有关，但没想到方程的列法，于是转战 dp，结果 dp 也没想到，最后之后写特殊情况骗分。

正解思路

本文博客链接：2023NOIP A层联测23 T2 涂鸦 - 彬彬冰激凌 - 博客园 (cnblogs.com)

考虑设 \(f_{mst}\)，为 \(n*m\) 个格被压成一个二进制 \(mst\)，转移到最终状态的期望花费。

可以列出方程

\[f_{mst}=\frac{\sum f_j + w}{2nm} \]

\(j\) 为 \(mst\) 通过一次变换可以到达的状态，\(w\) 为到这个状态的花费。

若 \(j\) 为最终状态，则 \(f_j=0\)。

可以暴力的高斯消元解方程组，时间复杂度 \(2^{3nm}\)。

后面的优化变得科学（玄学）起来。

如果某个状态 \(i\) 行 \(j\) 列与目标状态不同，那么在这个位置，一定要进行一次覆盖 \((1,1)\) 到 \((i,j)\) 的操作。

把所有的覆盖操作提取出来，发现覆盖的范围够成了一个阶梯形。

如图：

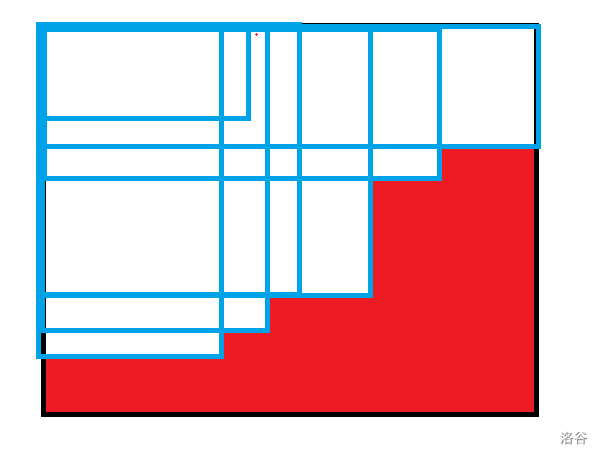
图中蓝色部分为一次覆盖操作，红色部分为与目标状态相同的部分。

这些覆盖操作有效的只有红蓝交界的覆盖。

why?

红蓝交界的覆盖表示了某个状态与目标状态红色状态相同，蓝色状态不同。而在蓝色部分内的覆盖如果执行了，那么相同部分会增加，也就是变成了别的红蓝状态。

我们可以发现，组成相同红蓝状态的原状态到目标状态的值是一样的。（因为都需要覆盖最外层，即交界的蓝色部分）

而红蓝状态的状态数较少，这样我们就缩小了状态数。

方程可以这么列：

1.得出红蓝状态，可以用二进制表示。

2.某个红蓝状态转回原状态。（任意转成一个即可，方便起见，红色部分与目标相同，蓝色部分与目标完全相反）

3.通过原状态暴力枚举操作，转移到其他的红蓝状态，列出方程。（方程类似于优化前的，相当于把原状态的未知数全部换成对于的红蓝状态的未知数。也就是说，一个红蓝状态对于多个原状态的未知数）

列出方程以后就可以愉快的高斯消元了。

#include<bits/stdc++.h>
using namespace std;

#define ll long long

const ll mod=998244353;
const int maxn=260;

int n,m,cnt,beg,fin,nn;

bool f[maxn];

ll a[maxn][maxn],val[maxn];

char st[10][10],ed[10][10];

unordered_map<int,int>mp;

vector<int>v;

ll ksm(ll x,ll y)
{
    int sum=1;
    for(;y;y/=2,x=x*x%mod) if(y&1) sum=sum*x%mod;
    return sum;
}
int gtid(int x,int y){return (x-1)*m+y;}

void dfs(int x,int k,int state)
{
    if(!x)
    {
        mp[state]=++cnt;
        v.push_back(state);
        return ;
    }
    for(int i=0;i<=k;i++) dfs(x-1,i,state|((1<<x*m)-1^(1<<x*m-i)-1));
}
int change(int id)
{
    int newid=(1<<n*m)-1;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if((id>>gtid(i,j)-1&1)!=(ed[i][j]=='B'))
            {
                for(int ii=1;ii<=i;ii++)
                {
                    for(int jj=1;jj<=j;jj++) newid&=INT_MAX^(1<<gtid(ii,jj)-1);
                }
            }
        }
    }
    return newid;
}

void gsxy()
{
    int r=1,c=1;
    for(;r<=nn&&c<=nn;r++,c++)
    {
        int mxid=r;
        for(int i=r+1;i<=nn;i++) if(abs(a[mxid][c])<abs(a[i][c])) mxid=i;
        for(int i=1;i<=nn+1;i++) swap(a[mxid][i],a[r][i]);
        if(abs(a[r][c])==0){r--;continue;}
        for(int i=1;i<=nn;i++)
        {
            if(i==r) continue;
            ll g=(a[i][c]*ksm((a[r][c]%mod+mod)%mod,mod-2)%mod+mod)%mod;
            for(int j=1;j<=nn+1;j++) a[i][j]=(a[i][j]-a[r][j]*g%mod+mod)%mod;
        }
    }
    memset(f,1,sizeof(f));
    for(int i=1;i<=nn+1;i++)
    {
        int ct=0,id=0;
        for(int j=1;j<=nn;j++) if(f[j]&&abs(a[i][j])) ct++,id=j;
        if(ct==1) f[id]=0,val[id]=(a[i][nn+1]*ksm(a[i][id]%mod+mod,mod-2)%mod+mod)%mod;
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%s",st[i]+1);
    for(int i=1;i<=n;i++) scanf("%s",ed[i]+1);
    dfs(n,m,0);
    for(int i=n;i;i--)
    {
        for(int j=m;j;j--)
        {
            fin=fin*2+(ed[i][j]=='B');
            beg=beg*2+(st[i][j]=='B');
        }
    }
    nn=v.size();
    for(int i=0;i<v.size();i++)
    {
        int t=v[i];
        if(i==mp[change(fin)]-1)
        {
            a[i+1][i+1]=1;
            continue;
        }
        int tt=0;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(t>>(gtid(i,j)-1)&1) tt|=(ed[i][j]=='B')<<(gtid(i,j)-1);
                else tt|=(ed[i][j]=='W')<<gtid(i,j)-1;
            }
        }
        a[mp[t]][mp[t]]+=2*n*m;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                int id=tt;
                for(int ii=1;ii<=i;ii++)
                {
                    for(int jj=1;jj<=j;jj++)
                    {
                        id|=1<<(gtid(ii,jj)-1);
                    }
                }
                a[mp[t]][nn+1]+=i*j;
                a[mp[t]][mp[change(id)]]--;
                for(int ii=1;ii<=i;ii++)
                {
                    for(int jj=1;jj<=j;jj++)
                    {
                        id^=1<<(gtid(ii,jj)-1);
                    }
                }
                a[mp[t]][nn+1]+=i*j;
                a[mp[t]][mp[change(id)]]--;
            }
        }
    }
    gsxy();
    printf("%lld\n",val[mp[change(beg)]]);
}

本题的代码逻辑复杂，写代码前可以想好或写下大概框架，在动键盘写代码，有效提升效率，减少错误。