给定一个长度为 \(n\) 的数组 \(a\),其中 \(a_i \in [-1, n]\),试计算满足以下条件的 \([1, n]\) 的排列 \(p\) 的个数:
- \(\forall i \in [1, n], \text{有 }\sum_{1 \le j \le i} [p_j \le i] = a_i \text{ 或 } a_i = -1\)
\(n \le 2 \times 10^5\)。
硬版本跟简单版本的区别就在于,存在 \(a_i = -1\),也就是对正方形内数字个数不做要求的情况。因此我们仍然可以借用简单版本的思路,将其放到二维平面上思考。
注意到 \(a_i = -1\) 的 \(i\) 对其他数字的放置不构成任何影响,那么我们只需要考虑 \(a_i \neq -1\) 的 \(i\) 即可。对于某个 \(i\),设 \(j < i\) 为离 \(i\) 最近的 \(a_j \neq -1\) 的 \(j\)(若不存在就设为 \(0\))。我们发现此时 \(d = a_i - a_j\) 不再满足 \(d \in \{0, 1, 2\}\) 的限制,且 L 形的宽度不再为 \(1\),因此好像不能借用 Easy Version 的思路分类讨论了。
举个例子,假设 \(a_4 = 2, a_5 = -1, a_6 = 5\),我们现在在填 \(i = 6\) 的格子,则有:
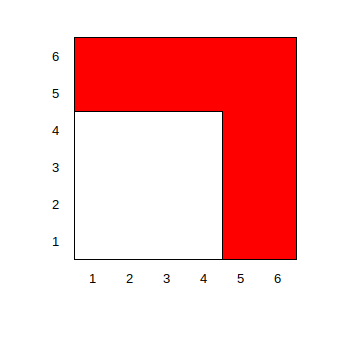
此时 L 形的宽度为 \(2\),且需要在 \(i, p_i \le 4\) 的区域放置两个点,那么我们很容易知道会有两行与两列的点受到影响。我们不关心具体是哪两行两列无法放置点,因此不失一般性的,我们假设是 \(1, 2\) 这两行两列无法放置。那么就有:
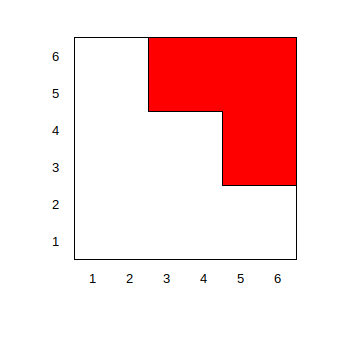
只有图中红色的部分是可用的。进一步的,我们将红色的部分划分为两个区域:
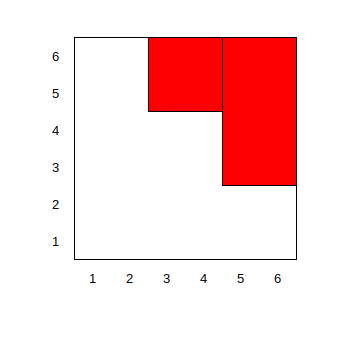
考虑枚举左边的矩形内放了多少个点,不妨设为 \(k\) 个,我们仍然不关心其被放置的具体位置,只需要知道,每放置一个点,右边部分的可用行,也就是纵坐标,就会减少 \(1\),那么我们可以将原问题抽象为在两个矩形内部放置点,例如,假设 \(k = 1\),那么左边的矩形长宽不变,而右边的矩形长度就会减一,那么也就是在一个长宽均为 \(2\) 的矩形(也就是左边的矩形)内部放置一个点,再在一个长为 \(3\),宽为 \(2\) 的矩形(也就是右边的矩形减掉一行)内部放置剩下的一个点。那么我们只需要知道在确定长宽的矩形内放置点的方案数即可。
设矩形的长为 \(h\),宽为 \(w\),需要放置的点数为 \(k\),为了保证没有同一行或者同一列上被放置了超过一个点,就需要先选出 \(k\) 个互不相同的行,方案数为 \(\binom{w}{k}\),再选出 \(k\) 个互不相同的列,方案数为 \(\binom{h}{k}\),最后再把这 \(k\) 行与 \(k\) 列两两配对,方案数为 \(k!\)。综上,选点的方案数就为 \(\binom{h}{k}\binom{w}{k}k!\)。
形式化的,对于某一对 \(i, j\),可以得到,左边的矩形的长宽分别为 \(i - j, j - a_j\),而右边的矩形长宽就分别为 \(i - j, i - a_j\)。设在左边的矩形内选 \(k\) 个点,则右边的矩形的长宽就会变为 \(i - j, i - a_j - k\)。因此,其方案数为:
那么只需要按顺序枚举 \(i\) 将每个 \(i\) 对应的答案垒乘起来即可。由于 \(\sum d = a_n - a_1 = \mathcal{O}(n)\),因此该做法的复杂度也是线性的。
- Permutation Problem Version 1909F Smallpermutation problem version 1909f permutation codeforces problem 1909i permutation codeforces problem version permutation codeforces another problem permutation another problem 1858c 题解permutation another problem 题解permutation abnormal version permutation problem 359 1909 1909d