简单地说，就是衡量两个概率分布之间的差异。也可以说是将一个概率分布转换成另一个概率分布要花费多少代价。


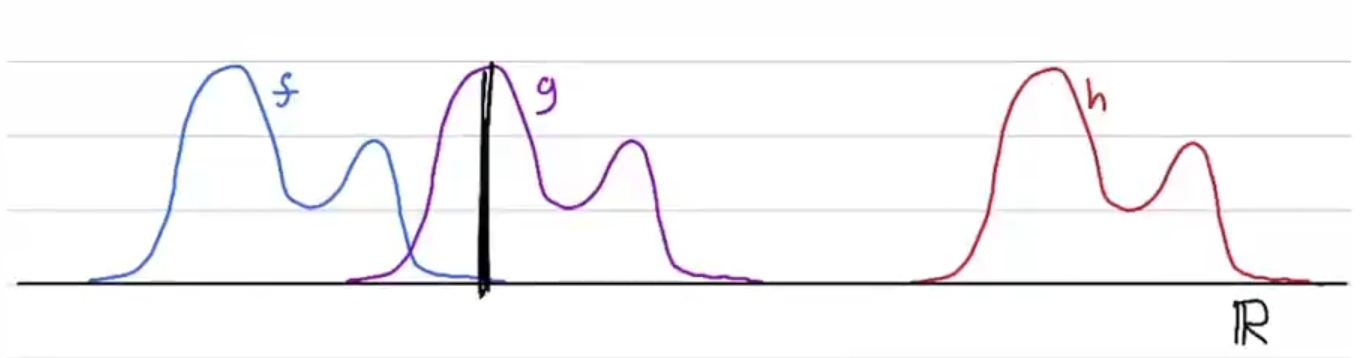
图1：在一维空间中的三个概率分布

比如，上图中有三个概率分布f, g, h，我们可以说f与g之间的距离比f与h之间的距离更小。

上述只是感性上的认知，那么如何计算出准确的数值呢？如果我们想求f与g之间差距，Wasserstein distance要求找到一种从f转移到g的方案，使得转移代价最小，用式子表示为：

\[\mathcal{W}[f, g]=\inf _{\gamma \in \Pi[f, g]} \iint \gamma({x}, {y}) d({x}, {y}) \mathrm d {x} \mathrm d {y} \]

这里\(\inf\)表示选择数值最小的方案，\(\Pi[f,g]\)表示所有\(f,g\)的转移方案的集合，\(\gamma\)是一种转移方案，\(d\)是自定义的距离计算方法。合起来的意思就是：从所有\(f\)到\(g\)的转移方案中，选择一个转移代价最小的方案，这个代价就是Wasserstein distance。

转移方案 Transport plan

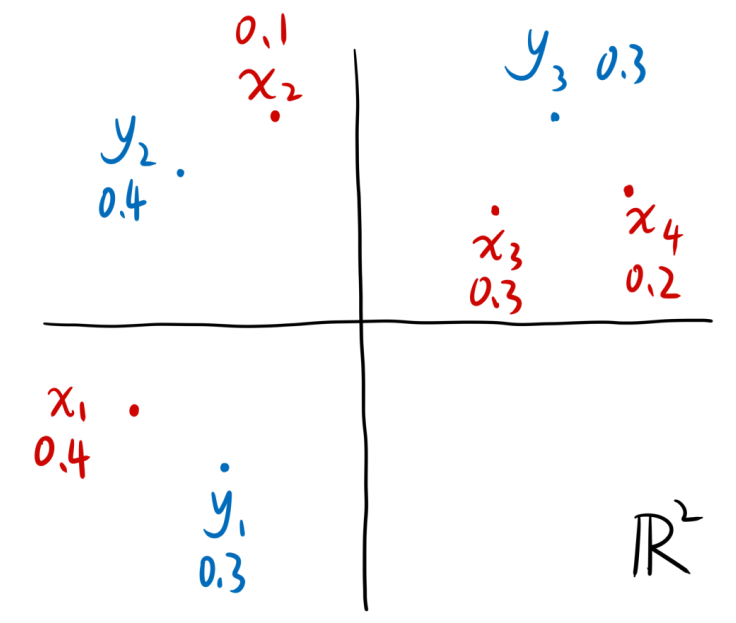
为了方便讲解什么是转移方案，我们假设两个概率分布分别如下所示


图2：在二维空间中的两个概率分布

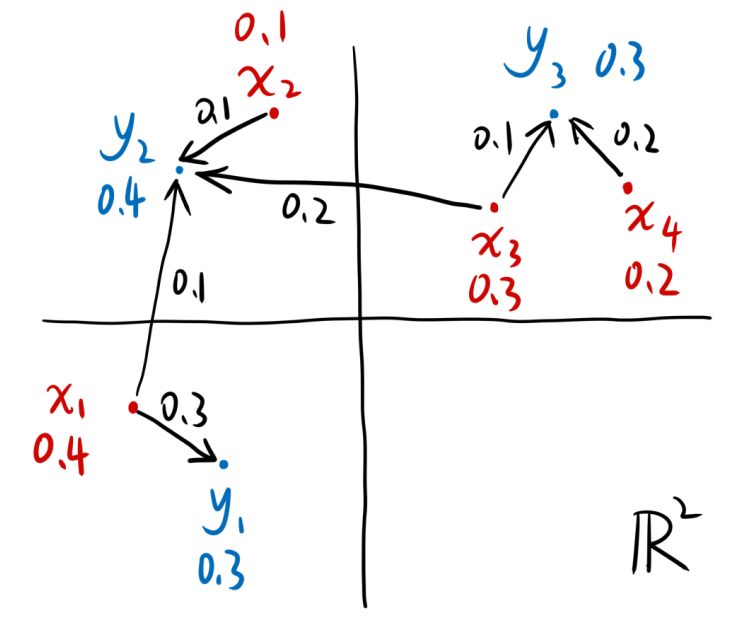
我们的目的是让x分布变成y分布，于是可以这样转移：


图3：从x到y的一种转移方案

例如\(y_2\)的0.4，是由\(x_1\)的0.1、\(x_2\)的0.1以及\(x_3\)的0.2组成的。总之，我们将这些转移关系列成一个表格，就是：


图4：从x到y的一种转移方案的表格

容易看出，这个表格实际上就是\(x\)和\(y\)的一个联合分布。也就是全部的值都是>=0的，每一列相加为对应的x值，每一行相加为对应的y值。

也就是说，从所有\(f\)与\(g\)的联合分布中，找到一个联合分布，使得以下式子的值最小：

\[\begin{array}{l} \displaystyle\inf_{\gamma \in \Pi[f, g]} \iint \gamma (x, y) d(x, y) \mathrm d x \mathrm d y \\ \text { s.t. }\left\{\begin{array}{l} \displaystyle\int \gamma(x, y)\mathrm d y=f(x) \\ \displaystyle\int \gamma(x, y)\mathrm d x=g(y) \\ \gamma (x, y) \geqslant 0 \end{array}\right. \end{array} \]

如何计算

我只看了两个离散的概率分布的距离如何计算。

据说python有一个库POT（Python Optimal Transport）可以用，具体的我并不了解。不过，这里我用一个例子，展示如何用线性规划计算两个离散概率分布的Wasserstein distance。

（可能用的符号不严谨，理解即可）
已知两个概率分布分别为\(X=\{x_1,\cdots,x_n\}\)和\(Y=\{y_1,\cdots,y_m\}\)，每两个元素之间的距离为\(D=\{d_{1,1},\cdots,d_{n,m}\}\)，其中\(d_{i,j}\)表示\(d(x_i,y_j)\)。
我们假设它们的联合概率分布为\(W=\{w_{1,1},\cdots,w_{n,m}\}\)，那么问题就是让\(\sum_{i,j}w_{i,j}d_{i,j}\)最小，即解下面这个线性规划问题：

\[ \begin{array}{l} \displaystyle\min\quad w_{1,1}d_{1,1}+w_{1,2}d_{1,2}+\cdots+w_{n,m}d_{n,m} \\ \text { s.t. }\left\{\begin{array}{l} \displaystyle\sum_j w_{1,j}=x_1 \\ \qquad\vdots \\ \displaystyle\sum_j w_{n,j}=x_n \\ \displaystyle\sum_i w_{i,1}=y_1 \\ \qquad\vdots \\ \displaystyle\sum_i w_{i,m}=y_m \\ w_{x,y} \geqslant 0 \end{array}\right. \end{array} \]

在论文DSTAGNN中，相应的代码是这样写的：

from scipy.optimize import linprog

def wasserstein_distance(p, q, D):
    A_eq = []
    for i in range(len(p)):
        A = np.zeros_like(D)
        A[i, :] = 1
        A_eq.append(A.reshape(-1))
    for i in range(len(q)):
        A = np.zeros_like(D)
        A[:, i] = 1
        A_eq.append(A.reshape(-1))
    A_eq = np.array(A_eq)
    b_eq = np.concatenate([p, q])
    D = np.array(D)
    D = D.reshape(-1)
    result = linprog(D, A_eq=A_eq[:-1], b_eq=b_eq[:-1])
    myresult = result.fun
    return myresult

代码的做法大致与上面相同，其中p,q分别是两个概率分布，D和我假设的意义相同，A_eq代表s.t.中等号左边的内容，b_eq代表s.t.中等号右边的数字。他没有写\(w_{x,y}\ge 0\)这个条件，可能默认就是这样的吧。
一个有意思的地方是，代码中A_eq和b_eq都舍掉了最后一个元素，也就是s.t.中的最后一个等号被忽略了。想一下也可以知道，只要前面的那些等式都保证了，最后一个等式是一定能保证的，所以不写也没问题。