[JLOI2016] 方
题目描述
上帝说,不要圆,要方,于是便有了这道题。
由于我们应该方,而且最好能够尽量方,所以上帝派我们来找正方形上帝把我们派到了一个有 \(N\) 行 \(M\) 列的方格图上,图上一共有 \((N+1)\times(M+1)\) 个格点,我们需要做的就是找出这些格点形成了多少个正方形(换句话说,正方形的四个顶点都是格点)。
但是这个问题对于我们来说太难了,因为点数太多了,所以上帝删掉了这 \((N+1)\times(M+1)\) 中的 \(K\) 个点。既然点变少了,问题也就变简单了,那么这个时候这些格点组成了多少个正方形呢?
保证 \(0 \le x \le N \le 10^6\),\(0 \le y \le M \le 10^6\),\(K \le 2000\) 且不会出现重复的格点。
思路点拨
可以看到 \(k\) 的值域是非常的小,这暗示我们可以考虑容斥。我们称被产出的点为 "坏点" ,那么答案就是:
这样子我们就可以将答案分成 \(5\) 个部分逐个击破。如果你还是想先自己思考,这里提醒一句, 正方形可以是斜着的 。(不要问我是怎么知道的,问就是 \(5\) 分)
至少包含 \(0\) 个坏点的正方形
也就是对网格图的所有正方形计数。先放出一张图:
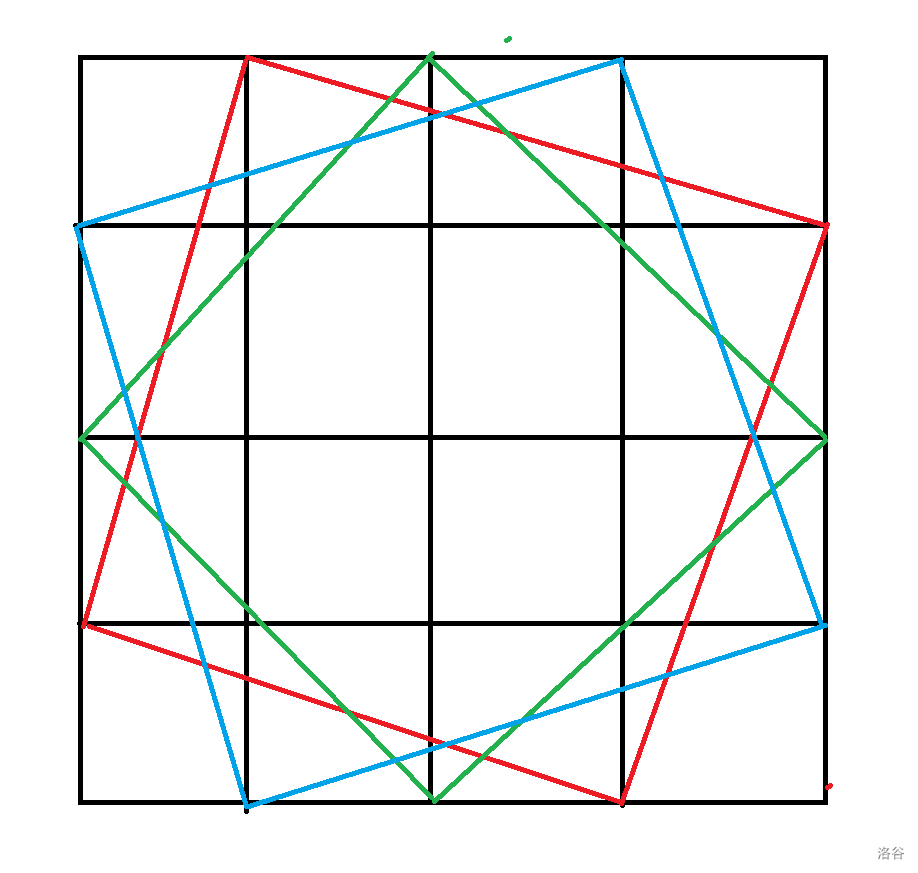
也是可以看到,一个边长为 \(i\) 的正方形,可以通过旋转得方式得到另外 \(i-1\) 个不同得正方形,加上自己就是 \(i\) 个正方形。我们就可以对于大正方形的边长计数,算出它可以旋转出多少个小的正方形,有:
这就是全部的正方形数量了。
至少包含 \(1\) 个坏点的正方形
这一点是本题的一个难点。既然至少有一个坏点,那么我们就先枚举是那个点吧。
对于每一个点,我们按照下图的方式将整个网格分成四个部分:
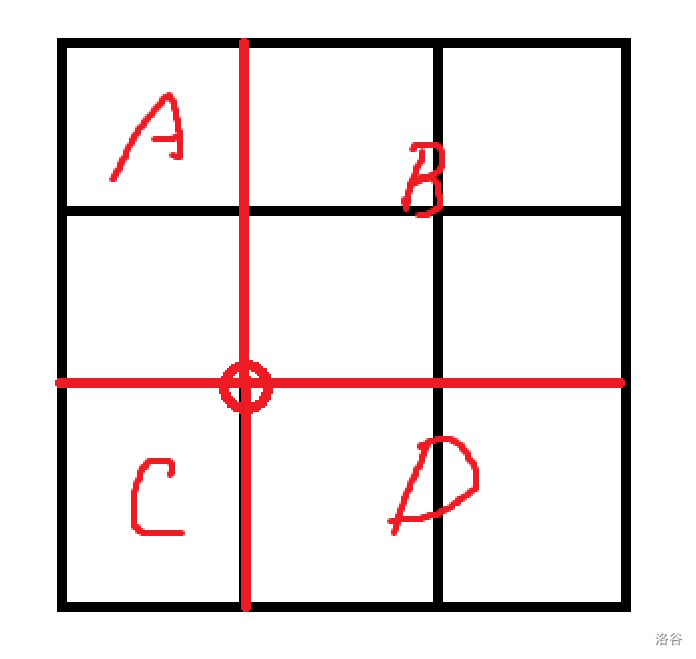
每一个坏点可以产生的贡献就是如下 \(8\) 个部分。
-
只有在 \(A\) 部分的正方形
-
只有在 \(B\) 部分的正方形
-
只有在 \(C\) 部分的正方形
-
只有在 \(D\) 部分的正方形
-
跨越了 \(AB\) 部分的正方形
-
跨域了 \(AC\) 部分的正方形
-
跨越了 \(BD\) 部分的正方形
-
跨越了 \(CD\) 部分的正方形
前四种都是十分好计数的,我们只讲后四种。我们发现,对于一个正方形,如果它跨越了两个部分,那么它一定是斜着的。如果一个斜正方形在 \(n\times m\) 网格内的,那么它有唯一个正着的大正方形包含着它,这个大正方形也在 \(n \times m\) 的网格内。可以自己画个图看一下,还是很好理解的。
接下来,我们就可以枚举那个大正方形来对斜着的正方形计数。这个正方形一定要跨越两个部分(一下按照 \(AB\) 部分的计数来讲) 。我们单纯的枚举正方形的边长(不用在意这会超时),可能会出现这个正方形在一个区域内的情况,我们可以进一步容斥,用全部的情况减去正方形在一个区域内的情况。看到下图 \(AB\) 部分,还有边长:
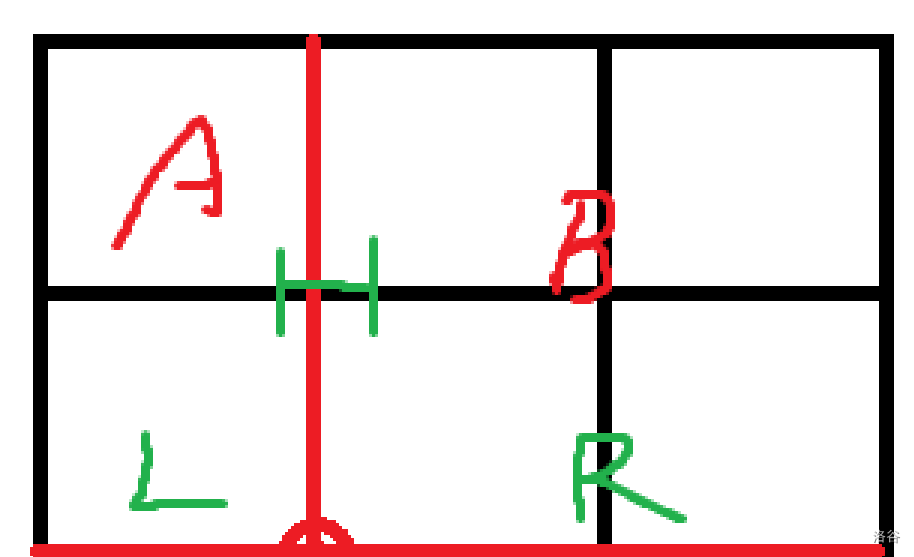
我们先讲到如何求解全部的正方形。显然我们枚举的边长 \(i\) 在 \(1\) 到 \(\min(H,L+R)\) 这个范围内。那么答案就是:
等差序列优化一下就是,首项是 \(L+R\) 末项是 \(L+R-\min(L+R,H)+1\) ,项数是 \(\min(L+R,H)\) 。就是:
接下来就是这个正方形只存在于某一个区域的情况。我们对于单个区域枚举(这部分讲述的是 \(B\) 区域),边长就是 \(R\) 。
那么这部分的答案就是
还是等差序列优化一下,首项是 \(R\) ,末项是 \(R-\min(R,H)+1\) ,项数就是 \(\min(R,H)\)
就是:
这部分我们就解决了。时间复杂度是 \(O(K)\) 。