题目大意
在平面上存在 \(n\) 个点,第 \(i\) 个点的坐标为 \((x_i,0)\),具有一个发射半径 \(r_i\) 和一个费用 \(v_i\)。
连接具有方向性,当且仅当 \(j<i\) 且点 \(i\) 的接收范围与点 \(j\) 的发射范围相切时点 \(i\) 才能连接到点 \(j\)。
第 \(i\) 个点的发射范围是指一个圆心在 \((x_i,r_i)\),半径为 \(r_i\) 的圆,接收范围是指一个圆心在 \((x_i,r_i')\),半径为 \(r_i'\) 的圆,其中 \(r_i'\) 可以被指定。
点 \(i\) 连接到点 \(j\) 的代价被定义为 \(\sqrt{r_i'}+v_i\),连接具有按方向的传递性,也就是说,若 \(a\) 连接到 \(b\),\(b\) 连接到 \(c\),那么 \(a\) 也连接到 \(c\)。
平面上还存在一个特殊点 \(u\),点 \(u\) 连接到点 \(j\) 的条件是 \(x_j+r_j\ge m\),且没有代价。求将点 \(u\) 连接到点 \(1\) 的最小代价。
思路分析
斜率优化 DP 好题。
设 \(f_i\) 表示考虑到第 \(i\) 个点,第 \(i\) 个点强制连接到某个点的最小代价。
考虑初值,有 \(f_1=v_1\)。考虑终值,所求即 \(\min\limits_{x_i+r_i\ge m} f_i\)。
枚举第 \(i\) 个点连接到的点 \(j\),容易得状态转移方程为:
其中,\(w(i,j)\) 表示将点 \(i\) 和点 \(j\) 连接的代价,即 \(r_i'+v_i\)。
\(r_i'\) 可以直接计算出来,根据勾股定理,有 \((r_i'-r_j)^2+(x_i-x_j)^2=(r_i'+r_j)^2\),容易解得 \(r_i'=\frac{(x_i-x_j)^2}{4r_j}\)。
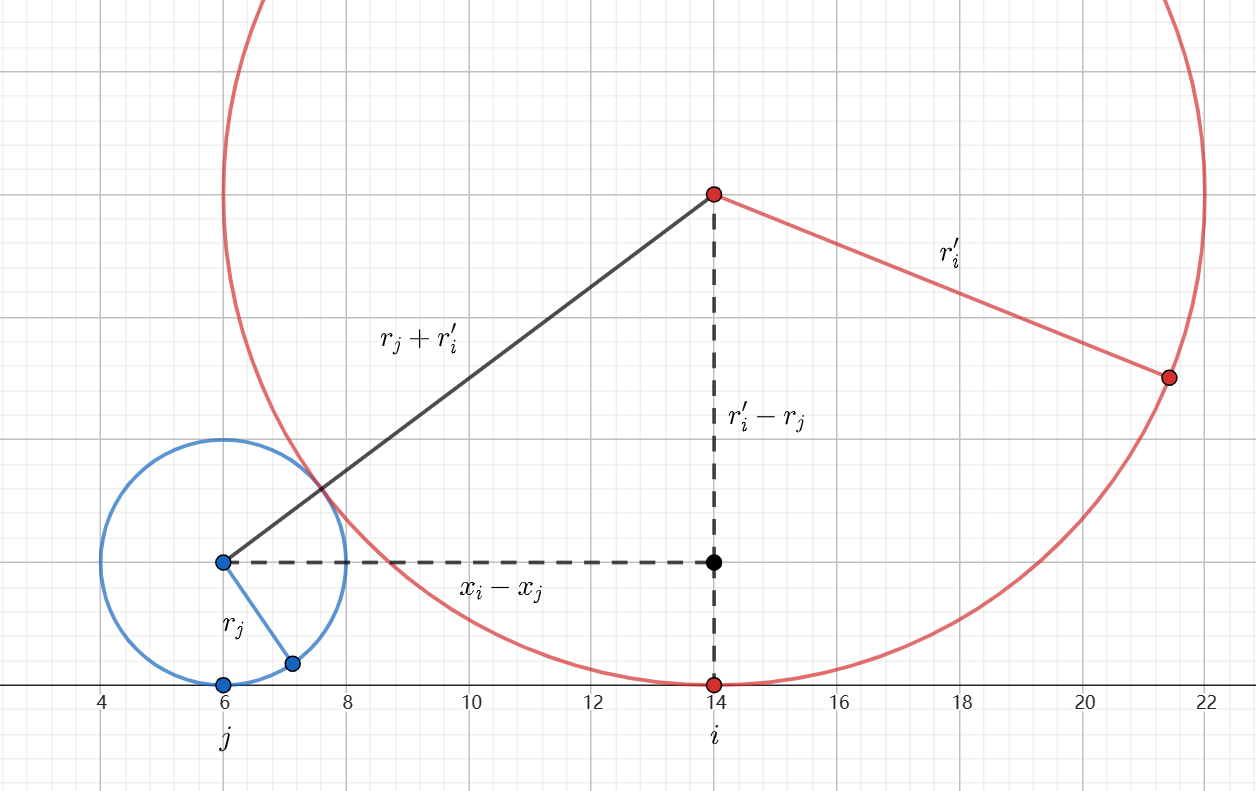
故 \(w(i,j)=\frac{x_i-x_j}{2\sqrt{r_j}}+v_i\)。
代入原方程,则:
然后是常规斜率优化化简:
设:
问题转化为每次插入一条 \(k_i=\frac{1}{2\sqrt{r_i}},b_i=f_i+\frac{x_i}{2\sqrt{r_i}}\) 的直线,查询 \(x=x_i\) 处的最小值,用李超线段树优化即可。
考虑到 \(x_i\) 的值域较大,可以对其离散化。
代码
#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N=500500;
#define inf 1e18
#define mid ((l+r)>>1)
int n,m;
int x[N],bx[N],r[N],v[N];
double f[N],ans=inf;
struct Line{
double k,b;
}line[N];
double calc(int id,int pos){//计算第 id 条直线在离散化后的 pos 处的值
return line[id].k*bx[pos]+line[id].b;
}
bool Less(int id1,int id2,int pos){//比较两条直线的优劣
return calc(id1,pos)<calc(id2,pos);
}
struct ST{//简洁的李超线段树
int a[N<<2];
void add(int p,int l,int r,int id){
if(l==r){if(Less(id,a[p],l)) a[p]=id;return ;}
if(Less(id,a[p],mid)) swap(a[p],id);
if(Less(id,a[p],l)) add(p<<1,l,mid,id);
if(Less(id,a[p],r)) add(p<<1|1,mid+1,r,id);
}
double query(int p,int l,int r,int pos){
double res=calc(a[p],pos);
if(l==r) return res;
if(pos<=mid) res=min(res,query(p<<1,l,mid,pos));
else res=min(res,query(p<<1|1,mid+1,r,pos));
return res;
}
}tree;
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&x[i],&r[i],&v[i]);
bx[i]=x[i];
}
int tot=unique(bx+1,bx+n+1)-bx-1;
for(int i=1;i<=n;i++)
x[i]=lower_bound(bx+1,bx+tot+1,x[i])-bx;//常规离散化
line[0]={0,inf};//将第 0 条线的值赋为无穷,可以省去特判空直线的情况
f[1]=v[1];//初始化
line[1]=Line{1/(2*sqrt(r[1])),f[1]-bx[x[1]]/(2*sqrt(r[1]))};
tree.add(1,1,n,1);//插入第一条直线
for(int i=2;i<=n;i++){
f[i]=tree.query(1,1,n,x[i])+v[i];
line[i]=Line{1/(2*sqrt(r[i])),f[i]-bx[x[i]]/(2*sqrt(r[i]))};
tree.add(1,1,n,i);//插入直线
}
for(int i=1;i<=n;i++)
if(bx[x[i]]+r[i]>=m) ans=min(ans,f[i]);//对所有满足条件的点取最小值
printf("%.3lf\n",ans);
return 0;
}