Codeforces Global Round 16(D,E,F)

D

还有一个简单版本的，我这里就直接看难的那一个版本的了

题目大意就是有\(n\times m\)个人需要去看电影，然后每个人都会依次进入电影院，但是他们的位置是有要求的，即视力弱的人会选择前面的位置（选择位置的索引越小），然后电影院的位置是这样子排布的

然后对于每一个人要到达他的位置过程中，我们需要计算出这个人从最左边到达他的位置这个过程会遇到多少个人，我们最后是输出所有人最后达到自己的位置的过程中会遇到的人的最小总量

如\(x\)要到第\(4\)个座位，但是前面的\(1\)和\(2\)都已经坐了人，那么\(x\)会遇见\(2\)个人

我的解法是一排一排来看

对于某一排，最后可以坐的是那些人我们是可以求出来的

但是还一种情况，当有若干个同样视力的人，这种视力的人既可以坐在\(x\)排的末尾，又可以坐在\(x+1\)的前面，我们可以先让可以让先走的人（选择作为相对较前）选择坐在\(x\)的末尾，让比较后走的选择在\(x+1\)的前面，这样可以减少遇到的人数

然后对于这一排的这\(m\)个人，谁先走，谁后走也有一个相对的顺序，就是原来的顺序（\(id\))的相对顺序，小的先走，大的后走，然后我们会有一个数组来记录这一排第\(i\)个走的人的视力

对于此时走的人的视力为\(now\)，那么在这之前出现的比\(now\)小的数量就是这个人会遇到的人数

但是由于视力的范围很大，但是每一排\(m\)的数量还不是很大，所以我们可以把这\(m\)个数进行离散化

然后求比\(now\)小的数使用树状数组即可

具体的操作就看代码吧

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include<cmath>
#include <unordered_map>
using namespace std;
#define int long long 
#define ios  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
const int maxn=4e5+10;
const int mod=1e9+7;
int n,t,m,num;
int c[maxn];
struct node
{
    int sum,id,pos;
}a[maxn],b[maxn];
int tx[maxn],ty[maxn];
bool cmp1(node x,node y)
{
    if(x.sum==y.sum)
    {
        return x.id<y.id;
    }
    return x.sum<y.sum;
}
bool cmp2(node x,node y)
{
    return x.id<y.id;
}
int lowbit(int x)
{
    return x&(-x);
}
void add(int x,int val)
{
    while (x<=m)
    {
        c[x]+=val;
        x+=lowbit(x);
    }
    return ;
}
int sum(int x)
{
    int res=0;
    while (x>0)
    {
        res+=c[x];
        x-=lowbit(x);
    }
    return res;
}
int query(int l,int r)
{
    int res=0;
    res=sum(r)-sum(l-1);
    return res;
}
void init()
{
    for (int i=1;i<=m;i++)
    {
        c[i]=0;
    }
    return ;
}
int get()
{
    init();
    int res=0;
    sort(tx+1,tx+1+m);
    int p=unique(tx+1,tx+1+m)-tx-1;
    for (int i=1;i<=m;i++)
    {
        int now=lower_bound(tx+1,tx+1+m,ty[i])-tx;
        add(now,1);
        if(now==1) continue;
        res+=query(1,now-1);
    }
    return res;
}
void solve()
{
    cin>>n>>m;
    num=n*m;
    int ans=0;
    for (int i=1;i<=num;i++)
    {
        cin>>a[i].sum;
        a[i].id=i;
    }
    sort(a+1,a+1+num,cmp1);
    int now=0;
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=m;j++)
        {
            b[j]=a[now+j];
        }
        sort(b+1,b+1+m,cmp2);
        for (int j=1;j<=m;j++)
        {
            tx[j]=b[j].sum;
            ty[j]=tx[j];
        }
        ans+=get();
        now+=m;
    }
    cout<<ans<<"\n";
    return ;
}
signed main ()
{
    cin>>t;
    while (t--)
    {
        solve();
    }
    system ("pause");
    return 0;
}

E

这个题的大意就是有\(n\)个点，\(m\)条边，然后有一个“芽”的定义，他们认为对于一个点，它的子节点都是叶子结点时，那么这个点就是芽

我们可以把一个芽和它的叶子结点重新连到除芽本是和它的叶子结点以外的所有点

然后我们可以观察案例

对于一个原本是这样的树

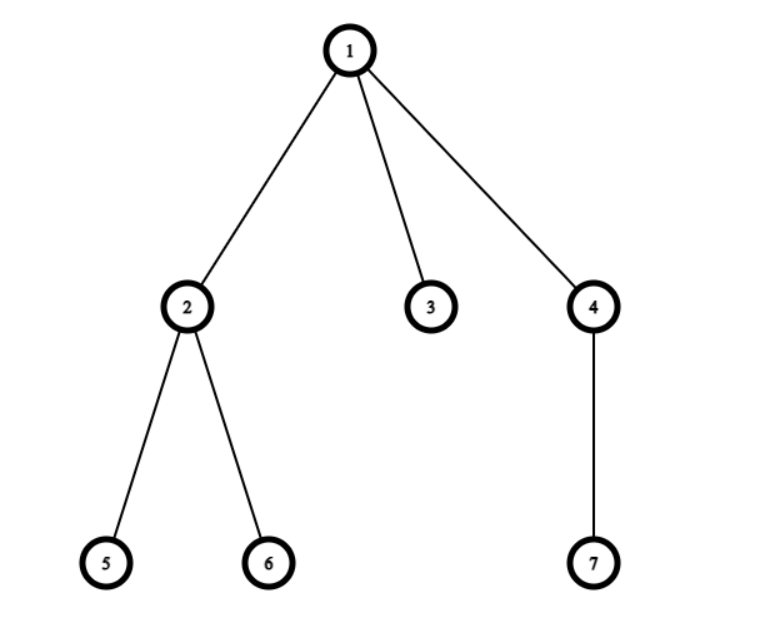
我们最终可以变成如下的树

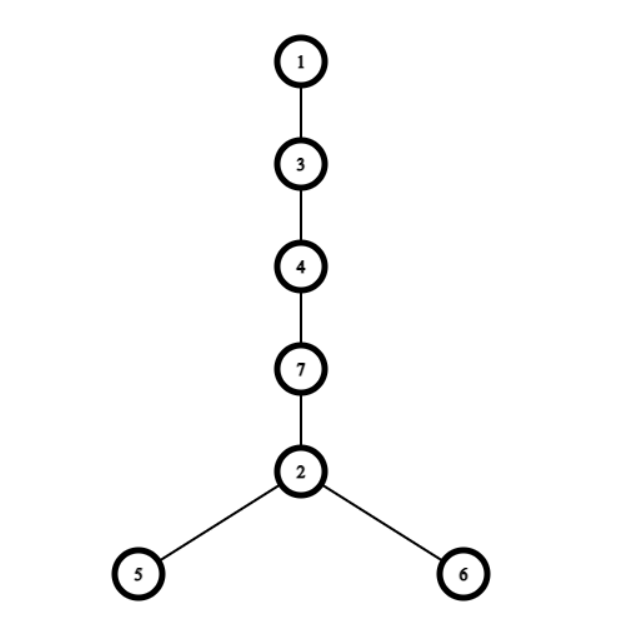
我们可以发现要想叶子结点少，我们之后都一定会有一条主干的，把那些分支都尽量变成主干

但是芽和叶子结点时一起的，那么芽里面就只能有一个芽在主干里面，其余的都是分支，只能作为叶子结点，只有那个作为主干的叶子结点才可能变成非叶子结点（如果后面有其他的芽连接）

那么最小的叶子结点数就是\(1\)加上所有的芽的叶子结点的数量减一的和

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include<cmath>
#include <unordered_map>
using namespace std;
#define ll long long 
#define ios  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
const int maxn=2e5+10;
const int mod=1e9+7;
int n,t,m;
vector<int>g[maxn];
int ans;
int dfs(int u,int fa)
{
    int res=0;
    for (auto v:g[u])
    {
        if(v==fa) continue;
        res+=dfs(v,u);
    }
    if(res==0)
    {
        return 1;
    }
    ans+=(res-1);
    return 0;
}
void solve()
{
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        g[i].clear();
    }
    for (int i=1;i<n;i++)
    {
        int u,v;
        cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    ans=1;
    dfs(1,0);
    cout<<ans<<"\n";
    return ;
}
signed main ()
{
   // ios;
    cin>>t;
    while (t--)
    {
        solve();
    }
    system ("pause");
    return 0;
}

F

这个题的大意就是有\(n\)个点，\(m\)条线段，只要有一个点在某一条线段里面，那么就算访问了这一条线段，每一个点移动一个单位的代价是\(1\),问这\(n\)个点访问完所有的线段需要的最小代价

我这个解法时间复杂度好像有点高，会卡\(long long\),所以一开始我用了\(#define int long long\)就一直超时，后面改了才过的

但是感觉解题过程还是很清晰的

首先对于那些已经访问过（线段里面本来就有点）的边就不需要再次访问了

 if(lower_bound(p,p+n+2,l)!=upper_bound(p,p+n+2,r))//对于这一条线段l,r,如果 l p1 r p2 这样的话，那么就可以知道这一条线段里面已经有点了
   {
            continue;
   }

还有对于那些线段可以被另外一条线段覆盖，那么可以不用考虑覆盖的那一条线段，反正都要到这条线段的內部

 sort(s.begin(),s.end(),cmp);//我们先把所有的线段按照右端点的从小到大排序，对于右端点一样的，按照左端端点从大到小排序
//那么对于两段线段，[l1,r1] [l2,r2]如果右端点一样，即r1==r2,那么l1>l2,那么是[l1,r1]覆盖[l2,r2]
//那么对于两段线段，[l1,r1] [l2,r2]如果右端点不一样，即r1<r2,只要存在l1>=l2,那么是[l1,r1]覆盖[l2,r2]
    for (int i=1;i<s.size();i++)
    {
        if(s[i-1].l>=s[i].l||s[i-1].r==s[i].r)
        {
            s.erase(s.begin()+i);
            i--;
        }
    }

然后才是考虑这些点的移动，我们对于它进行往左的移动还是往右的移动，在移动之后它是否还需要返回原来的位置

我们考虑的是对于两个点，去遍历这中间的所有线段，怎么分配（就是解决这个点是往左移多少，往右移多少的问题）

如此时有两个点\(x\)和\(y\),这中间有两条边\(s_1,s_2\),我们有以下三种选择

1.\(x\)点不动，\(y\)点最后往左移动到\(s_1\)的右边界

2.\(x\)点最后往右移动到\(s_1\)的左边界，\(y\)点最后往左移动到\(s_2\)的右边界

3.\(x\)点最后往右移动到\(s_2\)的左边界，\(y\)不动

但是我们不能只考虑这一次的访问，还有后面的\(s_3\),有可能也需要\(y\)的访问

所以我们还要记录\(x\)和\(y\)点是否回到原来的位置

对于前面一个点，上一次使用还未回到原来的位置，那么这一次要到达另外一个方向的移动的话，就只能是先往右移动，回来，然后再去访问前面的一条线段，这样就需要这一段距离乘以\(2\)

对于前面一个点，上一次使用回到原来的位置，我们只需要考虑这一次到达需要到的点的距离

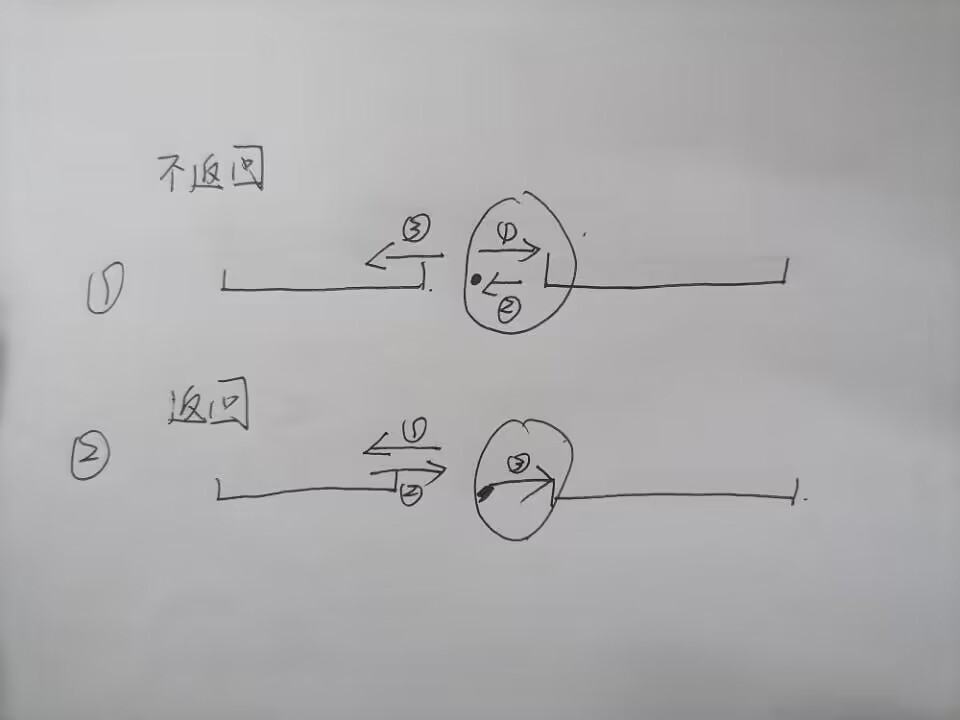
我们用\(dp[i] [0]\)来表示第\(i\)个点返回原来的位置，用\(dp[i] [1]\)来表示第\(i\)个点不返回原来的位置

因为每一次都是两个点之间的线段的选择，但是有可能有一些线段不在这些点的范围里，所以我们就增加了两个端点，最左端点\(p_0\),最右端点\(p_{n+1}\)

那么我们就可以得到状态转移方程

dp[i][0]=min(dp[i][0],dp[i-1][0]+(l[j]-p[i-1])+2*(p[i]-r[j]));
dp[i][1]=min(dp[i][1],dp[i-1][0]+(l[j]-p[i-1])+(p[i]-r[j]));
dp[i][0]=min(dp[i][0],dp[i-1][1]+2*(l[j]-p[i-1])+2*(p[i]-r[j]));
dp[i][1]=min(dp[i][1],dp[i-1][1]+2*(l[j]-p[i-1])+(p[i]-r[j]));

然后具体的就看代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include<cmath>
#include <unordered_map>
using namespace std;
#define ll long long 
#define ios  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
const int maxn=4e5+10;
const int mod=1e9+7;
int n,t,m;
struct node 
{
    int l,r;
}a[maxn];
ll p[maxn];
bool cmp(node x,node y)
{
    if(x.r!=y.r)
    {
        return x.r<y.r;
    }
    return x.l>y.l;
}
void solve()
{
    cin>>n>>m;
    for (int i=1;i<=n;i++)
    {
        cin>>p[i];
    }
    p[0]=-1e10,p[n+1]=1e10;
    sort(p,p+n+2);
    vector<node>s;
    for (int i=1;i<=m;i++)
    {
        int l,r;
        cin>>l>>r;
        if(lower_bound(p,p+n+2,l)!=upper_bound(p,p+n+2,r))
        {
            continue;
        }
        s.push_back({l,r});
    }
    sort(s.begin(),s.end(),cmp);
    for (int i=1;i<s.size();i++)
    {
        if(s[i-1].l>=s[i].l||s[i-1].r==s[i].r)
        {
            s.erase(s.begin()+i);
            i--;
        }
    }
    vector<vector<ll>>dp(n+3,vector<ll>(3,1e15));
    dp[0][0]=dp[0][1]=0;
    int now=0;
    for (int i=1;i+1<=n+2;i++)
    {
        vector<ll>l,r;
        l.push_back(p[i-1]);
        while (now<s.size()&&s[now].r<p[i])
        {
            l.push_back(s[now].l);
            r.push_back(s[now].r);
            now++;
        }
        r.push_back(p[i]);
       for (int j=0;j<l.size();j++)
        {
            dp[i][0]=min(dp[i][0],dp[i-1][0]+(l[j]-p[i-1])+2*(p[i]-r[j]));
            dp[i][1]=min(dp[i][1],dp[i-1][0]+(l[j]-p[i-1])+(p[i]-r[j]));
            dp[i][0]=min(dp[i][0],dp[i-1][1]+2*(l[j]-p[i-1])+2*(p[i]-r[j]));
            dp[i][1]=min(dp[i][1],dp[i-1][1]+2*(l[j]-p[i-1])+(p[i]-r[j]));
        }
    }
    ll ans=min(dp[n+1][0],dp[n+1][1]);
    cout<<ans<<"\n";
    return ;
}
signed main ()
{
    ios;
    cin>>t;
    while (t--)
    {
        solve();
    }
    system ("pause");
    return 0;
}