定义与性质
笛卡尔树是一种二叉树,每一个结点由一个键值二元组 \((k,w)\) 构成。要求 \(k\) 满足二叉搜索树的性质,而 \(w\) 满足堆的性质。
,也就是说,对于一个节点 \(i\) 的左儿子 \(l_i\) 和右儿子 \(r_i\),一定满足 \(l_i<i<r_i\)(下标 \(k\) 满足二叉搜索树的性质)且 \(v_{l_i}\) 与 \(v_{r_i}\) 同时不大于或不小于 \(v_i\)(权值 \(w\) 满足堆的性质)。若序列的权值互不相同,则笛卡尔树形态唯一。
这里给出 OI Wiki 的一张图,可以看到一个子树对应的下标一定是连续的。
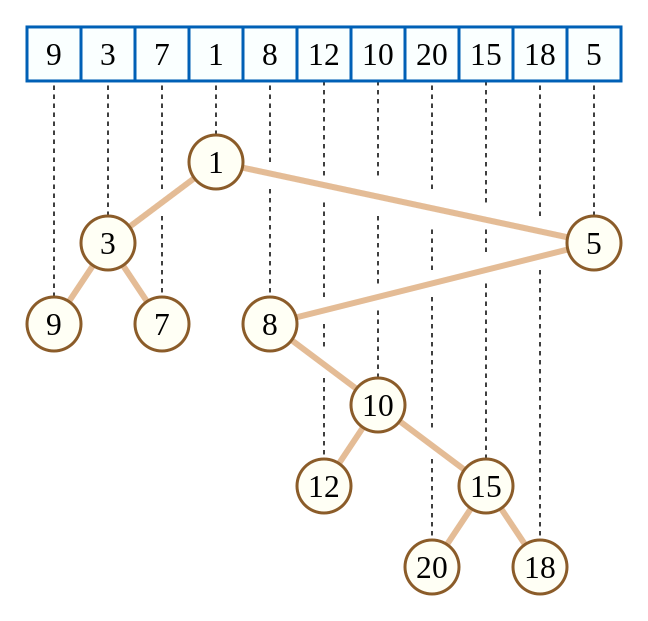
- 假设是最小堆,如上图,一个节点(不妨设其下标为 \(i\))在笛卡尔树上的祖先节点由 \(v_1∼v_i\) 形成的单调递增的单调栈以及 \(v_i∼v_n\) 形成的单调递减的单调栈内所有元素组成。因此,笛卡尔树又可以看作两个单调栈。
建树方法
不妨假设我们要构建满足大根堆性质的笛卡尔树。
考虑使用增量法,从左到右依次加入序列中的每个值,维护一个递减的单调栈表示当前笛卡尔树最靠右的链。这和虚树的构建比较类似。
加入一个下标为 \(i\) 的值 \(v\) 时,首先找到单调栈中最小的且大于 \(v\) 的值 \(w\),设其对应节点为 \(u\),那么将 \(u\) 的右儿子改成 \(i\),将 \(i\) 的左儿子改成 \(u\) 原来的右儿子(即单调栈中 \(u\) 上方的元素),再将 i 压入栈即可。
const int N = 1e7 + 67;
int stc[N], top, a[N], ls[N], rs[N];
void build(){
for(int i = 1; i <= n; ++i){
while(top && a[stc[top]] < a[i]) ls[i] = stc[top--];
rs[stc[top]] = i, stc[++top] = i;
}
}
例题
Ⅰ. P6604 [HNOI2016] 序列 加强版
\(f_i\) 表示以 \(i\) 结尾的子序列的最小值之和,令 \(pre_i\) 为 \(i\) 之前第一个比 \(a_i\) 小的下标。
显然 \(f_i = f_{pre_i} + (a_i \times (i - pre_i))\) 。
发现 \(pre_i\) 其实是 \(i\) 在笛卡尔树上的第一个左拐的祖先。可以模拟笛卡尔树建树过程来求解 \(pre_i\)。
对于一个区间的答案, 求出区间最小值的位置 \(p\):
-
那么左端在 \(p\) 左边,右端在 \(p\) 右边的子区间最小值 为 \(a_p\), 这部分答案 \(a_p \times (p - l + 1) \times (r - p + 1)\)
-
在 \((p, r]\), 发现每个位置 \(i\) 对答案的贡献为 \(f_i - f_p\)。
-
在 \([l,r)\), 同理,只需预处理出\(g_i\) 表示全局以\(i\) 开头的子区间的最小值之和并类似处理即可。
2、3 前缀和优化即可。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define mp make_pair
#define fi first
#define se second
using namespace std;
const int N = 1e5 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
bool _u;
int n, q, type, top;
int a[N], lg[N], mi[20][N], pre[N], suf[N], stc[N];
ll fp[N], fs[N], gp[N], gs[N];
ll res;
int get_min(int x, int y){return a[x] > a[y] ? y : x;}
int RMQ(int l, int r){int d = lg[r - l + 1]; return get_min(mi[d][l], mi[d][r - (1 << d) + 1]);}
bool _v;
int main(){
cerr << abs(&_u - &_v) / 1048576.0 << "MB\n";
n = read(), q = read();
for(int i = 1; i <= n; ++i) a[i] = read(), mi[0][i] = i;
for(int i = 2; i <= n; ++i) lg[i] = lg[i >> 1] + 1;
for(int i = 1; i <= lg[n]; ++i)
for(int j = 1; j + (1 << i) - 1 <= n; ++j)
mi[i][j] = get_min(mi[i - 1][j], mi[i - 1][j + (1 << i - 1)]);
for(int i = 1; i <= n; ++i){
while(top && a[stc[top]] >= a[i]) suf[stc[top--]] = i; //类比笛卡尔树建树 ls[i] = stc[top--]
// 因为 stc[] 维护的是右链, 所以在 i 往上跳的过程中,经过的点第一个右拐的祖先都是 i
pre[i] = stc[top], stc[++top] = i; //同样 rs[stc[top]] = i
// i 是 stc[top] 的右儿子, 所以 stc[top] 是 i 的第一个左拐的祖先
}
for(int i = 1; i <= n; ++i) fp[i] = fp[pre[i]] + 1ll * a[i] * (i - pre[i]), gp[i] = gp[i - 1] + fp[i];
for(int i = n; i; --i) fs[i] = fs[suf[i]] + 1ll * a[i] * (suf[i] - i), gs[i] = gs[i + 1] + fs[i];
for(int i = 1, l, r; i <= q; ++i){
l = read(), r = read();
ll p = RMQ(l, r), ans = 0;
ans = 1ll * a[p] * (p - l + 1) * (r - p + 1);
ans += gp[r] - gp[p] - 1ll * fp[p] * (r - p);
ans += gs[l] - gs[p] - 1ll * fs[p] * (p - l);
cout << ans << endl;
}
return 0;
}
Ⅱ.CF1117G Recursive Queries
转化题意后发现,对于\([l,r]\) 所在的点建立笛卡尔树,求每个点的子树大小的和
设 \(L_i\) 为 \(i\) 左边第一个大于 \(a_i\) 的位置, \(R_i\) 为 \(i\) 右边一个大于 \(a_i\) 的位置。如果没有设为 \(0 / n + 1\) 。
发现答案就是 \(\sum\limits_{i = l}^{r} \min(r, R_i - 1) - \max(l, L_i + 1) + 1\)
\(R_i\) 和 \(L_i\) 可以用笛卡尔树求出,如上题。
将答案拆成 max 和 min 两部分来算,考虑将 r 从 n 拖到 1 的过程中,每个点究竟对应 \(R_i−1\) 还是 \(r\) 只会改变一次。因此将询问离线下来,对于对应 \(R_i−1\) 的部分,直接树状数组维护查询区间 \(R_i−1\) 的和,而对于对应 \(r\) 的部分,再开一个树状数组维护有多少个对应 \(r\) 的数,区间求和并乘以 \(r\) 即可。
#include<bits/stdc++.h>
#define ll long long
#define pii pair<int, int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
using namespace std;
const int N = 1e6 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
bool _u;
int n, top, q;
int a[N], l[N], r[N], stc[N], p[N];
ll ans[N];
vector<pii> qu[N];
vector<int> buc[N];
struct BIT{
ll c[N];
void clear(){memset(c, 0, sizeof(c));}
void add(int x, int v){for(; x <= n; x += x & -x) c[x] += v;}
ll ask(int x){ll res = 0; for(; x; x -= x & -x) res += c[x]; return res;}
ll query(int l, int r){return ask(r) - ask(l - 1);}
}t1, t2;
bool _v;
int main(){
cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
n = read(), q = read();
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 1; i <= q; ++i) l[i] = read();
for(int i = 1; i <= q; ++i) r[i] = read(), qu[r[i]].pb(mp(l[i], i));
for(int i = n; i; --i){ // 寻找右边第一个大于 a[i] 的位置
while(top && a[stc[top]] < a[i]) --top;
p[i] = top ? stc[top] : n + 1; stc[++top] = i;
buc[p[i] - 1].pb(i), t1.add(i, p[i] - 1);
}
for(int i = n; i; --i){
for(auto it : qu[i]) ans[it.se] += t1.query(it.fi, i) + t2.query(it.fi, i) * i;
for(auto it : buc[i]) t1.add(it, 1 - p[it]), t2.add(it, 1);
}
t1.clear(), t2.clear(), top = 0;
for(int i = 1; i <= n; ++i) qu[i].clear(), buc[i].clear();
for(int i = 1; i <= q; ++i) qu[l[i]].pb(mp(r[i], i));
for(int i = 1; i <= n; ++i){ // 寻找左边第一个大于 a[i] 的位置
while(top && a[stc[top]] < a[i]) --top;
p[i] = top ? stc[top] : 0; stc[++top] = i;
buc[p[i] + 1].pb(i), t1.add(i, p[i] + 1);
}
for(int i = 1; i <= n; ++i){
for(auto it : qu[i]) ans[it.se] -= t1.query(i, it.fi) + t2.query(i, it.fi) * i;
for(auto it : buc[i]) t1.add(it, -1 - p[it]), t2.add(it, 1);
}
for(int i = 1; i <= q; ++i) printf("%lld ", ans[i] + r[i] - l[i] + 1); printf("\n");
return 0;
}
Ⅲ.AT_agc028_b [AGC028B] Removing Blocks
随机一个排列,代价的期望 \(\times n!\) 就是答案。
考虑计算每个元素在某一个固定顺序中,贡献到代价中的次数。建立基于删除时间的小根笛卡尔树,则笛卡尔树上一个节点对答案的贡献是子树内 \(a_i\) 之和。
子树贡献转成深度贡献,那么代价为 \(\sum_{i = 1} ^ {n} h_i \times a_i\)。
那么现在就是要计算 \(E(h_i)\)。
考虑排列, 若 \(x < i\) 且 \(x\) 为 \(i\) 的祖先,如果只看 \(x \sim i\) 内的数的话,那么其余所有数被删去的顺序对答案没有影响, 因为要 \(x\) 先删除,所以合法的排列 \(\frac{(i - x)!}{(i - x + 1) !} = \frac{1}{i - x + 1}\),期望加上即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 67, mod = 1e9 + 7;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
bool _u;
int n, ans;
int a[N], inv[N], sum[N];
bool _v;
signed main(){
cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
n = read(); inv[1] = 1;
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 2; i <= n; ++i) inv[i] = inv[mod % i] * (mod - mod / i) % mod;
for(int i = 1; i <= n; ++i) sum[i] = (sum[i - 1] + inv[i]) % mod;
for(int i = 1; i <= n; ++i) (ans += (sum[i] + sum[n - i + 1] - 1) * a[i]) %= mod;
for(int i = 1; i <= n; ++i) ans = ans * i % mod;
printf("%lld\n", ans);
return 0;
}
Ⅳ.CF1580D Subsequence
按 \(a_i\) 建出笛卡尔树,显然树形 DP ,设 \(f[i][j]\) 表示到 \(i\) 号点,选了 \(j\) 个点。
对于 \(x\) 点,我们可以看成三部分: \(x / ls[x] / rs[x]\) ,树上背包即可。
\(f[x][i + j] = \max(f[x][i + j], f[x][i] + f[y][j] - 2 \times i \times j \times a[x])\)。 \(i\) 倒叙, \(j\) 正序。
#include<bits/stdc++.h>
#define pb push_back
#define ll long long
using namespace std;
const int N = 4e3 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
bool _u;
int n, m, top;
int a[N], stc[N], sz[N], ls[N], rs[N];
ll f[N][N];
void dfs(int x){
f[x][1] = 1ll * (m - 1) * a[x], sz[x] = 1;
auto solve = [&] (int y){
dfs(y);
for(int i = sz[x]; ~i; --i)
for(int j = 0; j <= sz[y]; ++j)
f[x][i + j] = max(f[x][i + j], f[x][i] + f[y][j] - 2ll * i * j * a[x]); // 因为有 i * j 种的区间最小值为 a[x]
sz[x] += sz[y];
};
if(ls[x]) solve(ls[x]);
if(rs[x]) solve(rs[x]);
}
bool _v;
int main(){
cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
n = read(), m = read();
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 1; i <= n; ++i){
while(top && a[stc[top]] > a[i]) ls[i] = stc[top--];
rs[stc[top]] = i, stc[++top] = i;
}
int rt = stc[1];
dfs(rt), printf("%lld\n", f[rt][m]);
return 0;
}