AVL树
AVL树又称二叉平衡树,是为了改良二叉查找树,因树的性质问题而导致形成单链或者不平衡,深度更深,深度遍历效率低而提出的一种改进。
1.平衡因子
平衡因子顾名思义其实是测评一个二叉树节点的平衡关系,平衡度,而提出的一个性质,在这里需要先理解树的高度和深度这一概念.
为了方便理解,先给出深度和高度的定义:
高度:指该节点到叶子节点的最长节点数
深度:从根节点到该节点的节点数(因为这个路径是唯一的,所以不存在最长)
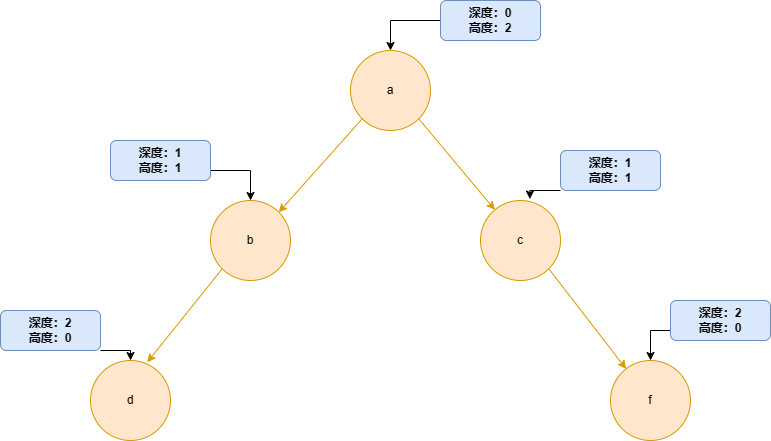
平衡因子则是左右子树的高度差,左子树的高度减去右子树的高度得到
例如:如果出现非平衡的二叉树则是这样的:
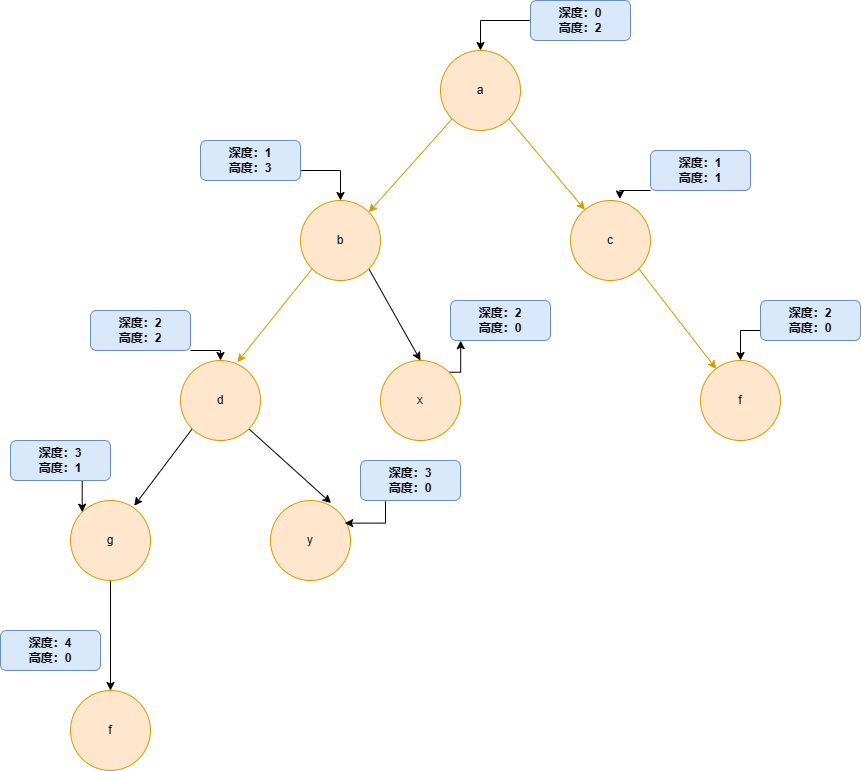
因此对于节点B来说,此时就是不平衡的,他的子树d和x的高度差的绝对值大于了1,因此需要调整,同样由于对于节点A来说,他也是不平衡的,所以有时候·旋转可能就不止一次,最多不超过2次,是因为在所有节点在平衡的时候都不会平衡因子都不会超过这个度量,也就是1,因此下一次添加节点,必定是叶子节点,也就是会增加跟这个叶子节点相关路径的所有节点的深度,此时出现平衡因子可能就不止2,甚至3的情况也有可能(这里说的是绝对值).
2.AVL树节点
这里用JAVA实例去书写AVL树代码,任何一种编程语言其实都能实现:
class AVLNode<K extends Comparable<K>, V> {
K key;
V value;
int height;
AVLNode<K, V> left;
AVLNode<K, V> right;
public AVLNode(K key, V value) {
this.key = key;
this.value = value;
this.height = 1;
this.left = null;
this.right = null;
}
}
3.返回节点高度
private int getHeight(AVLNode<K, V> node) {
if (node == null) {
return 0;
}
return node.height;
}
结点中有hegitht属性,如果node为null,则返回0.
每次添加节点则有可能影响节点的高度,因此实现方法:
private void updateHeight(AVLNode<K, V> node) {
if (node == null) {
return;
}
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
高度是到叶子节点的最长路径,只能深度向下遍历,因为节点是依次添加的,所以递归得到结果+1.
4.计算节点的平衡因子
这个代码的实现也很简单:
private int getBalanceFactor(AVLNode<K, V> node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
5.插入
这个方法的实现核心思想就是将需要插入的节点插入到合适的位置并做出调整.
public void insert(K key, V value) {
root = insert(root, key, value);
}
-
所以插入时需要先判断是否为第一个节点,即根节点,如果是根节点,则立刻将key,value赋值给root
if (node == null) { return new AVLNode<>(key, value); } -
如果根节点存在,则判断插入的位置,这个需要根据cmp,也就是比较器去自定义,通常来说左边小,右边大,也可以左大右小.
int cmp = key.compareTo(node.key); if (cmp < 0) { node.left = insert(node.left, key, value); } else if (cmp > 0) { node.right = insert(node.right, key, value); } else { // 若 key 已存在,则更新 value node.value = value; return node; }这里通过递归的方式深度遍历节点.
-
因为插入节点,所以高度需要更新
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));这一步必须在递归完成之后再去更新,也就意味着处插入的节点外,其余节点都会去更新其高度,而高度的更新顺序则是从离插入节点最近的方向向根节点方向进行,因此高度不会出现错误.
-
插入之后要获取每个节点的平衡因子
// 平衡节点 int balanceFactor = getBalanceFactor(node);- 注:这里需要知道因为平衡因子:是通过左子树高度-右子树高度得到的,因此就会出现三种不同的情况,差大于1,差小于-1,等于0,因为高度的值只可能是1,2,3.因此
if (balanceFactor > 1) { // } else if (balanceFactor < -1) { // }接下来面对大于1,小于-1分别讨论:
-
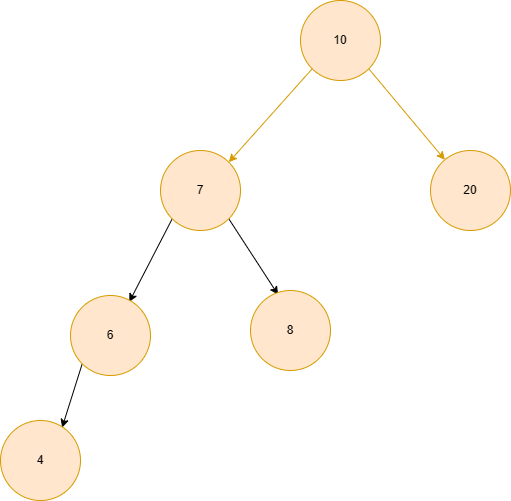
平衡因子大于1,意味着左子树的高度大于右子树的高度,如图所示:
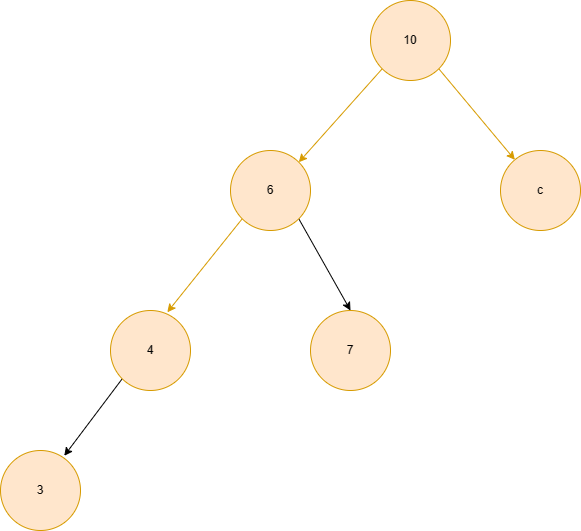
对于根节点10来说,他的平衡因子就是2,因此左子树明显比右子树多上一层,意味着对于节点为6的这个子树整体不平衡(是相较于他的父亲节点10而言的),而这种展露方式其实也是LL类型,也就是左子树臃肿,同样在子树中也是因为左子树臃肿导致,所以称为LL,为什么这么说呢,因为对于子树6而言,他的平衡因子是1,有着大于1的趋势,整体向左倾斜,因此无论3节点是位于4节点的左边还是4节点的右边(当然,3不能位于4的右边,但是假如一个大于4的节点放到了右边)这种类型也依然是LL类型,我想传达的就是这个意思,因此存在LL型就存在LR型,因此如果在节点7的左子树或右子树存在节点,同时节点4不存在子节点,就会出现LR型。
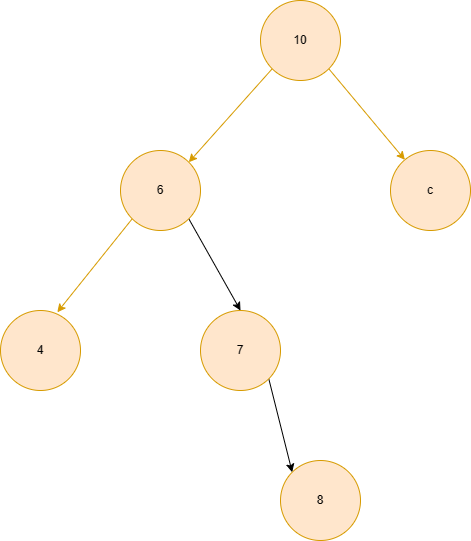
还是那个意思,能理解就行。
if (key.compareTo(node.left.key) < 0) { // LL 情况,左左情况,需要进行右旋转 return rightRotate(node); } else { // LR 情况,左右情况,需要进行左旋转后再右旋转 node.left = leftRotate(node.left); return rightRotate(node); } -
反之,则是RR和RL型,道理和逻辑是互通的,在这里展示图片和代码:
if (key.compareTo(node.right.key) > 0) { // RR 情况,右右情况,需要进行左旋转 return leftRotate(node); } else { // RL 情况,右左情况,需要进行右旋转后再左旋转 node.right = rightRotate(node.right); return leftRotate(node); }
RR型
RL型因此判断为这四种类型之后就需要进行旋转了,也就是核心的平衡思想,另外平衡因子为0的情况下,说明左右子树很平衡,不需要进行什么操作。
6.旋转
旋转的核心思想在于如何将平衡因子控制在-1~1,也就是那种树之间的高度差如何消除到1,拿LL树举例说明,此时左子树臃肿,右子树空闲,而对于6这颗子树而言,无论再怎么旋转(言外之意就是相对于父亲节点,自身已经不平衡了,在自己的领地再怎么折腾,他都不无法改变事实,因此他需要和父节点协商,让他做父亲(言外之意就是牺牲一下父节点的地位,保全这种平衡关系)也就让左子树上升,右子树下降的这种旋转思维去实现。
具体该如何实现呢?不难发现,作为6节点的子树的右节点必然是小于6节点的父亲节点并且小于6节点的(不然也插不进去啊),这就意味着7号节点(其实这里说子树更准确)作为6节点的父亲节点的左节点。也就是右旋转
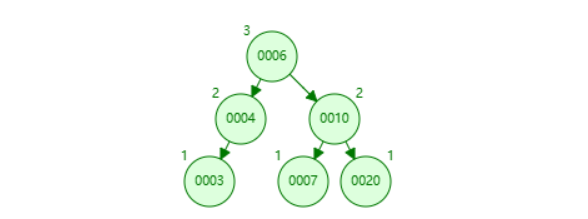
那LR型也也可以通过这种方式进行旋转吗?
其实无论是LL还是LR这个子树的臃肿都是相对于10号这个节点的,也就是平衡因子大于1的这个节点,但是对于6节点本身来讲,自身右子树有臃肿的趋势,如果按照之前的移动,则会导致10节点的左子树出现不平衡.所以此时的旋转是让6节点本身的右子树(因为是LR型)的第一个节点做自己的父亲节点,而叶子节点(即左子树中最大的节点)做父亲节点的左子树.
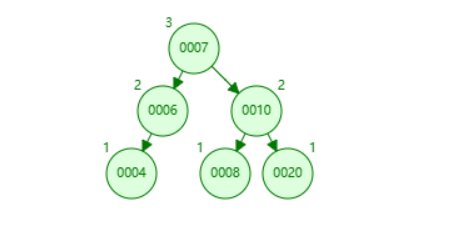
而在面对LR型时,我们发现应当先处理自身不平衡的趋势,再去处理父节点对于子树的不平衡,而因为节点6的子树趋向于右子树,所以应当选择左旋转,所以其实本质上旋转只有两种操作,左和右,而面对不平衡趋向采取不同的旋转方式,如果向左倾斜,则整体右转,一次即可,如果自身先向右倾斜,再宏观上向左倾斜,则需要先左转之后再进行右转,因此LR型,其实有一个中间态的过程,就是进行了左转.
那么RR类型就意味着需要左旋,左旋其实和右旋的逻辑是相反的,也就是移动自身,让自身成为子树的左右孩子,同时添加之前子树的左右孩子添加给自己,因此左旋转就是将父节点变为子树的左孩子,将子树的左节点赋值给父节点的右子树(拿前面图举例:14大于10小于20,因此让他作为父节点的右孩子).
RL类型则是通过先右转再左转的方式,其实做的都是一系列一个本质的事情.
总结:
左转:让对于有不平衡子树的一方(也就是高度更高的一方),将根节点的左子树赋值给自己的父亲节点的右子树,将自己的位置和父亲的位置互调.
右转:让对于有不平衡的子树的一方(也就是高度更高的一方),将根节点的右子树赋值给自己父亲节点的左子树,将自己的位置和父亲的位置互调.
因此代码实现:
// 左旋转
private AVLNode<K, V> leftRotate(AVLNode<K, V> node) {
AVLNode<K, V> newRoot = node.right;
node.right = newRoot.left;
newRoot.left = node;
// 更新节点的高度
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
newRoot.height = 1 + Math.max(getHeight(newRoot.left), getHeight(newRoot.right));
return newRoot;
}
// 右旋转
private AVLNode<K, V> rightRotate(AVLNode<K, V> node) {
AVLNode<K, V> newRoot = node.left;
node.left = newRoot.right;
newRoot.right = node;
// 更新节点的高度
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
newRoot.height = 1 + Math.max(getHeight(newRoot.left), getHeight(newRoot.right));
return newRoot;
}
而旋转之后由于平衡因子减小,因此节点的高度需要更新和变化(其实只会影响父节点和子树的根节点),这里的newRoot指向的是有不平衡趋势的子树的根节点,而node则是他的父节点(父节点的平衡因子是大于1小于-1的).
7.删除
删除操作大致和插入操作如出一辙,因为删除和插入其实都是在做一件事,改变树的高度,所以在每次做完相应的操作(删除要找到对应的位置,插入也是如此).之后在对树的类型做出判断,然后选择相应的旋转,不过在删除的时候需要注意是叶子节点还是非叶子节点的问题,也就是是否为中继节点,如果是中继节点,那么需要对左右子树进行处理,如果是叶子节点删了就删了.大致就是如此了.