斜率优化
dp回顾
对于所有的方程都需要枚举 \(j = [l, i - 1]\)
- \(dp[i] = max/min(dp[j] + a[i])\) 维护出前缀的最值即可
- \(dp[i] = max/min(dp[j] + a[j])\) 维护出前缀的最值即可
- \(dp[i] = max/min(dp[j] + a[j] + a[i])\) 维护出前缀的最值即可
- \(dp[i] = max/min(dp[j] + a[i] * b[j])\)
特殊:\(a[i] * b[j]\) 是否存在单调性,\(a,b\) 数组本身是单调的
而斜率优化可优化的dp类型就是第四种
P3195 [HNOI2008]玩具装箱
分析
设 \(dp[i]\) 表示到 \(i\) 为止的最小花费
对于 \(dp[i]\) 枚举所有的 \(1 \leq j < j\)
\(dp[i] = min(dp[j] + (\sum{C_{[j+1,i]}}+i-j-1-L)^2)\)
\(dp[i] = min(dp[j] + (sum[i] - sum[j] + i - j - 1 - L)^2)\)
\(dp[i] = min(dp[j] + (sum[i]+ i - sum[j] - j - 1 - L)^2)\)
设 \(F[i] = sum[i] + i\)
\(dp[i] = min(dp[j] + (F[i] - F[j] - 1 - L)^2)\)
这个方程就满足上面所说的第4类方程,就可以用到斜率优化
斜率优化
需要先把方程推导出斜率的公式 \(\frac{\Delta{y}}{\Delta{x}}\)
-
自己设置两个决策点 \(j_1\) 和 \(j_2(j_1 < j_2)\) 并且 \(j_2\) 优于 \(j_1\)
代入这两个决策点到方程中,推导什么样条件满足 \(j_2\) 优于 \(j_1\)
\(dp[j_1] + (F[i] - F[j_1] - 1 - L)^2 >= dp[j_2] + (F[i] - F[j_2] - 1 - L)^2\) -
拆开不等式,把不等式变成斜率的形式
\(dp[j_1] + F[i]^2 - 2 * F[i] * (F[j_1] + 1 + L) + (F[j_1] + 1 + L)^2\)
\(>= dp[j_2] + F[i]^2 - 2 * F[i] * (F[j_2] + 1 + L) + (F[j_2] + 1 + L)^2\)\(2 * F[i] * (F[j_2] + 1 + L) - 2 * F[i] * (F[j_1] + 1 + L)\)
\(>= dp[j_2] + (F[j_2] + 1 + L)^2 - (dp[j_1] + (F[j_1] + 1 + L)^2)\)\(2 * F[i] * (F[j_2] - F[j_1]) >= dp[j_2] + (F[j_2] + 1 + L)^2 - (dp[j_1] + (F[j_1] + 1 + L)^2)\)
\(2 * F[i] >= \frac{dp[j_2] + (F[j_2] + 1 + L)^2 - (dp[j_1] + (F[j_1] + 1 + L)^2)}{F[j_2] - F[j_1]}\)
设 \(G[i] = (F[i] + 1 + L)^2\),代入
\(2 * F[i] >= \frac{(dp[j_2] +G[j_2]) - (dp[j_1] + G[j_1])}{F[j_2] - F[j_1]}\) -
显然我们可以把 \(F[j]\) 看做 \(x\) 横坐标,\(dp[j] + G[j]\) 看做 \(y\) 纵坐标,那么右边的式子也就变成了一个斜率 \(k=\frac{\Delta{y}}{\Delta{x}}\),也就是说 \(k <= 2 * F[i]\),决策点 \(j_2\) 优于 \(j_1\)
-
在决策点 j 依次向右移动的过程中,只有保证单调递增,所有的 j 才有可能成为最优决策点
如果存在三个决策点 \(j_1,j_2,j_3\) 出现 \(k(j_1,j_2)\)的斜率大于 \(k(j_2,j_3)\) 的斜率,那么 \(j_2\) 必然不可能成为最优决策点
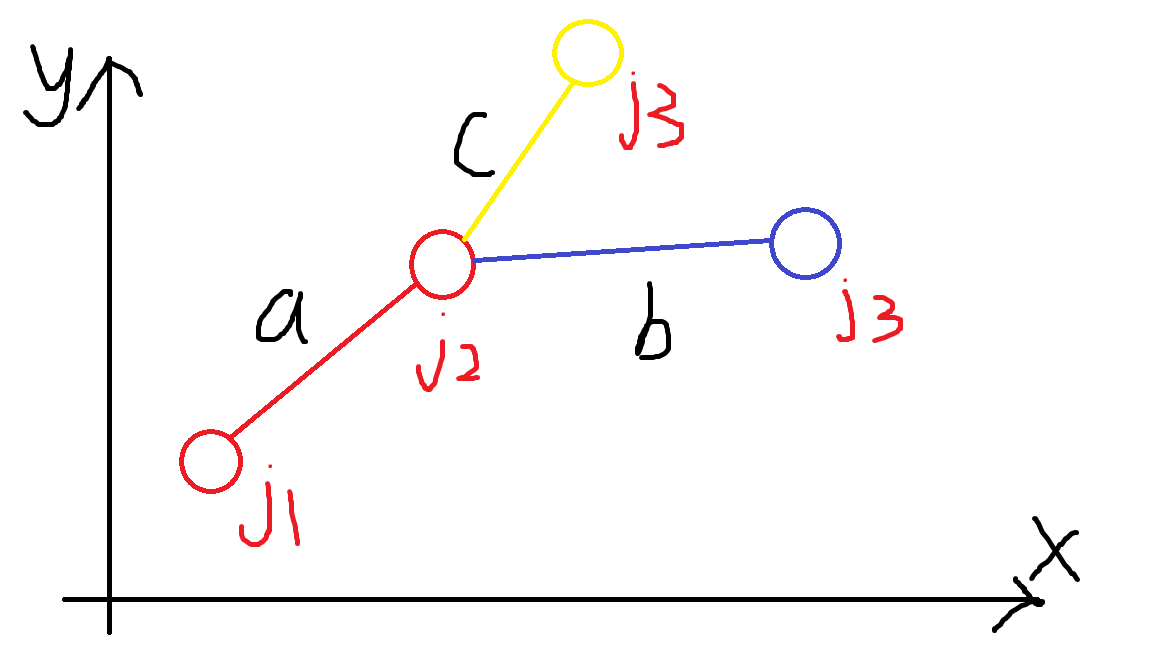
也就是说,
当\(j_3\)在黄色点时,\(c \gt a\) 此时无论\(2 * F[i]\)是多大,\(j_1,j_2,j_3\)都有可能成为最有决策点
而当\(j_3\)在蓝色点位置时,则\(a \gt b\),\(j_2\)是不可能成为最有决策点的,因为无论什么情况,\(j_3\)都会比\(j_2\)优,所以直接可以把\(j_2\)删除,这样所得到的序列就是单调的了 -
寻找答案,只需要二分查找维护出来的斜率队列,找到最大的那个满足条件的斜率,这个斜率所对应的右端点即为最优决策点 \(j\)
当然,这里也可以直接用单调队列来维护决策点队列
如果 \(i\) 和队首两个点的斜率 \(< 2 * F[i]\) 则删除队首
对于队尾两个点的斜率大于当前 \(i\) 和队尾的斜率,则删除队尾
代码
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=5e4+10;
int n,head,tail;
ll a[maxn],sum[maxn],F[maxn],L,G[maxn],dp[maxn];
int dq[maxn];
double K(int j1,int j2){
return (double)(dp[j1]+G[j1]-dp[j2]-G[j2])/(F[j1]-F[j2]);
}
int main(){
/*2023.4.30 hewanying P3195 [HNOI2008]玩具装箱 斜率优化dp*/
scanf("%d%lld",&n,&L);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
sum[i]=sum[i-1]+a[i];
F[i]=sum[i]+i;
G[i]=(F[i]+1+L)*(F[i]+1+L);
}
G[0]=(L+1)*(L+1); //把G[0]当作原点,可以不用判断队伍中只有一个元素的情况
for(int i=1;i<=n;i++){
while(head<tail&&K(dq[head],dq[head+1])<2*F[i]) head++;
dp[i]=dp[dq[head]]+(F[i]-F[dq[head]]-1-L)*(F[i]-F[dq[head]]-1-L);
while(head<tail&&K(dq[tail-1],dq[tail])>K(dq[tail],i)) tail--;
dq[++tail]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
总结
- 斜率优化的题目一般代码都比较短,\(n^2\)的dp都比较好推,难就难在推公式的过程
- 在dp中可以常常设一些函数来表示固定的值,从而可以简化dp的式子,防止出现错误,如例题中的\(F[i],G[i]\)
- 注意初始化和是否要使用long long