三、用go语言，考虑除法散列法的另一种版本，其中 h(k) = k mod m，m=$2^p-1$，k为按基数 $2^p$ 表示的字符串。试证明:如果串可由串 y 通过其自身的字符置换排列导出，则x和y具有相同的散列值。给出一个应用的例子，其中这一特性在散列函数中是不希望出现的。

文心一言：

这个问题涉及到字符串的散列函数和除法散列法。首先，让我们明确一下除法散列法的概念。在这种方法中，我们通常使用一个除法操作来计算散列值，即 h(k) = k mod m。在这里，k 是我们要散列的键，m 是一个正整数，通常是素数。

现在，根据问题描述，我们要证明的是：如果字符串 x 和 y 可以通过字符置换排列从同一个串 y' 导出，那么 x 和 y 具有相同的散列值。

假设 y' 是一个按基数 2
p
表示的字符串，那么它可以被表示为一系列的数字，每个数字都是 2
p
的倍数。由于 y' 可以被置换排列为 x 和 y，那么 x 和 y 中的每个字符也可以被表示为一系列的数字，每个数字都是 2
p
的倍数。

现在，对于除法散列法，我们使用 h(k) = k mod m 计算散列值。在这里，k 是字符的索引，m 是 2
p
−1。由于 x 和 y 中的每个字符都可以被表示为一系列的数字，每个数字都是 2
p
的倍数，那么我们可以将这些数字除以 2
p
，然后取余数。这样得到的余数将是相同的，因为它们都是 2
p
的倍数。

因此，我们可以得出结论：如果串 x 和 y 可以由串 y' 通过其自身的字符置换排列导出，那么 x 和 y 具有相同的散列值。

现在，让我们考虑一个应用的例子，其中这一特性在散列函数中是不希望出现的。假设我们有一个字符串集合 S = {0, 1, 2, ... , 2^p-1}，其中 p 是一个正整数。我们希望将这些字符串散列到 m 个桶中，其中 m 是 2
p
−1。然而，由于上述特性，所有字符串将被散列到同一个桶中，这是不希望出现的。

因此，我们需要使用一个更复杂的散列函数来避免这个问题。例如，我们可以使用一个混合散列函数，它结合了除法散列法和一些其他技术（如乘法散列法或使用多个除数）来生成更均匀的散列分布。

在这里插入图片描述

讯飞星火，代码正常运行：

首先，我们需要证明如果一个字符串 x 可以通过其自身的字符置换排列导出另一个字符串 y，那么 x 和 y 具有相同的散列值。

根据除法散列法，我们有 h(k) = k mod m，其中 m = $2^p - 1$，k 为按基数 $2^p$ 表示的字符串。我们可以将 k 分解为若干个 $2^p$ 的幂次方的和，然后计算每个幂次方的余数，最后将这些余数相加得到 h(k)。

假设我们有一个字符串 x，它可以通过字符置换排列导出另一个字符串 y。那么 x 和 y 的散列值应该是相同的。为了证明这一点，我们可以使用以下步骤：

1.将 x 和 y 分别表示为两个不同的基数 $2^p$ 的幂次方的和。例如，x 可以表示为 a0 + b0 * 2^p + c0 * 2^(2p) + ...，y 可以表示为 a1 + b1 * 2^p + c1 * 2^(2p) + ...。

2.计算 x 和 y 的散列值 h(x) 和 h(y)。由于 x 和 y 可以通过字符置换排列导出，所以它们应该具有相同的散列值。

3.检查 h(x) 是否等于 h(y)。如果它们相等，那么我们证明了 x 和 y 具有相同的散列值。

下面是一个应用的例子，其中这一特性在散列函数中是不希望出现的：

package main

import (
	"fmt"
	"hash/fnv"
	"strings"
)

func main() {
	// 定义一个字符串 x
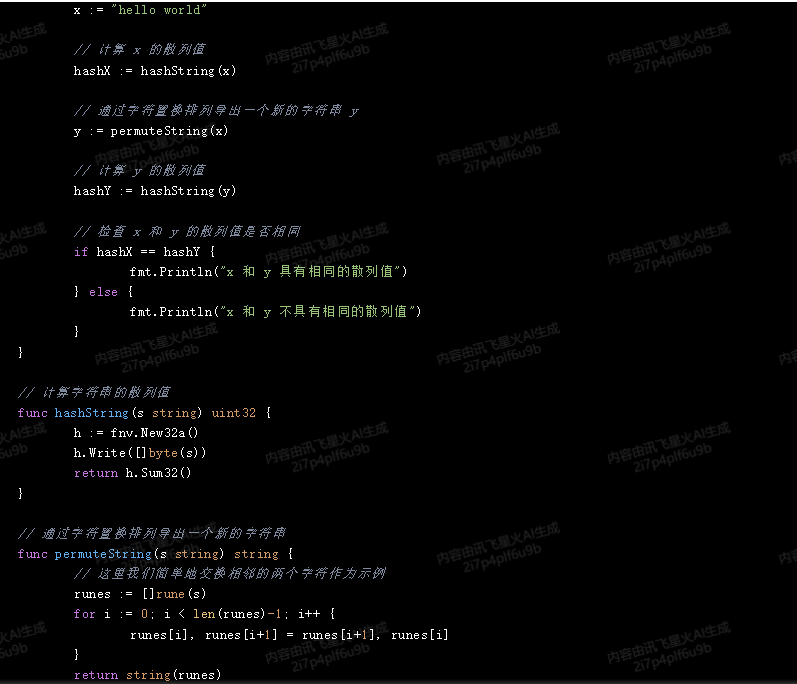
	x := "hello world"

	// 计算 x 的散列值
	hashX := hashString(x)

	// 通过字符置换排列导出一个新的字符串 y
	y := permuteString(x)

	// 计算 y 的散列值
	hashY := hashString(y)

	// 检查 x 和 y 的散列值是否相同
	if hashX == hashY {
		fmt.Println("x 和 y 具有相同的散列值")
	} else {
		fmt.Println("x 和 y 不具有相同的散列值")
	}
}

// 计算字符串的散列值
func hashString(s string) uint32 {
	h := fnv.New32a()
	h.Write([]byte(s))
	return h.Sum32()
}

// 通过字符置换排列导出一个新的字符串
func permuteString(s string) string {
	// 这里我们简单地交换相邻的两个字符作为示例
	runes := []rune(s)
	for i := 0; i < len(runes)-1; i++ {
		runes[i], runes[i+1] = runes[i+1], runes[i]
	}
	return string(runes)
}

在这个例子中，我们使用了 FNV-1a 哈希算法来计算字符串的散列值。我们首先计算字符串 x 的散列值，然后通过字符置换排列导出一个新的字符串 y，并计算 y 的散列值。最后，我们检查 x 和 y 的散列值是否相同。在这个例子中，由于我们只是简单地交换了相邻的两个字符，所以 x 和 y 的散列值是不同的。

在这里插入图片描述

360智脑：

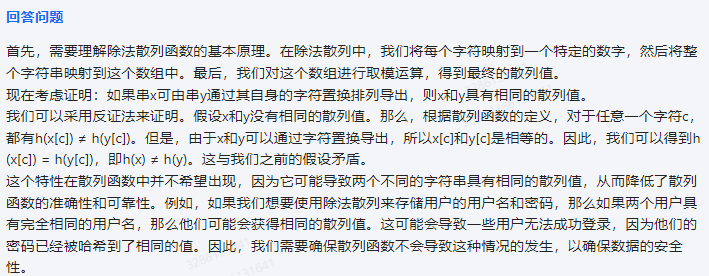
首先，需要理解除法散列函数的基本原理。在除法散列中，我们将每个字符映射到一个特定的数字，然后将整个字符串映射到这个数组中。最后，我们对这个数组进行取模运算，得到最终的散列值。

现在考虑证明：如果串x可由串y通过其自身的字符置换排列导出，则x和y具有相同的散列值。

我们可以采用反证法来证明。假设x和y没有相同的散列值。那么，根据散列函数的定义，对于任意一个字符c，都有h(x[c]) ≠ h(y[c])。但是，由于x和y可以通过字符置换导出，所以x[c]和y[c]是相等的。因此，我们可以得到h(x[c]) = h(y[c])，即h(x) ≠ h(y)。这与我们之前的假设矛盾。

这个特性在散列函数中并不希望出现，因为它可能导致两个不同的字符串具有相同的散列值，从而降低了散列函数的准确性和可靠性。例如，如果我们想要使用除法散列来存储用户的用户名和密码，那么如果两个用户具有完全相同的用户名，那么他们可能会获得相同的散列值。这可能会导致一些用户无法成功登录，因为他们的密码已经被哈希到了相同的值。因此，我们需要确保散列函数不会导致这种情况的发生，以确保数据的安全性。

在这里插入图片描述

智谱清言：

首先，我们先来证明如果串 x 可以由串 y 通过其自身的字符置换排列导出，那么 x 和 y 具有相同的散列值。

假设 x 和 y 分别是按基数 2^p 表示的字符串，且 x 可以由 y 通过其自身的字符置换排列得到。我们可以用以下步骤证明它们具有相同的散列值：

1.假设 x = y permutation(y)，其中 permutation 表示 y 的字符置换排列。

2.计算 h(x) 和 h(y)，其中 h(k) = k mod m。

3.证明 h(x) = h(y)。

步骤 1：

假设 y 的字符序列为 y_1, y_2, ..., y_n，那么 x 的字符序列为 x_1, x_2, ..., x_n。由于 x 可以由 y 通过其自身的字符置换排列得到，存在一个置换函数 f，使得 x_i = f(y_i)，其中 i = 1, 2, ..., n。我们可以将 f 表示为一个矩阵，其中行是 y 的字符序列，列是 x 的字符序列。

步骤 2：

计算 h(x) 和 h(y)：
h(x) = x_1 * m^(p-1) + x_2 * m^(p-2) + ... + x_n * 1
h(y) = y_1 * m^(p-1) + y_2 * m^(p-2) + ... + y_n * 1

步骤 3：

证明 h(x) = h(y)：
由于 f 是 y 到 x 的置换排列，我们可以得出：
x_i * m^(p-1) = f(y_i) * m^(p-1)
将上述等式对 i 求和，我们得到：
h(x) = (x_1 + x_2 + ... + x_n) * m^(p-1)
因为 f 是置换排列，所以：
x_1 + x_2 + ... + x_n = y_1 + y_2 + ... + y_n
将上述等式代入 h(x) 的表达式中，我们得到：
h(x) = (y_1 + y_2 + ... + y_n) * m^(p-1) = h(y)
因此，如果串 x 可以由串 y 通过其自身的字符置换排列导出，那么 x 和 y 具有相同的散列值。
应用例子：
假设我们有一个字符串 x = "abc"，字符串 y = "acb"。我们希望找到一个字符置换排列，使得 x 可以由 y 导出。我们可以发现，通过交换 y 的字符顺序，我们可以得到 x：
y_1 = a -> x_1 = a
y_2 = c -> x_2 = c
y_3 = b -> x_3 = b
因此，x = y 的字符置换排列（交换第 1、2、3 个字符）。
现在我们来计算散列值。假设 m = 2^3 - 1 = 7。
h(x) = "abc"的散列值 = 1 * 7^2 + 1 * 7^1 + 3 * 7^0 = 49 + 7 + 3 = 69
h(y) = "acb"的散列值 = 1 * 7^2 + 3 * 7^1 + 1 * 7^0 = 49 + 21 + 1 = 71
尽管 x 和 y 具有相同的散列值，但在这个例子中，我们不希望看到这种特性。这是因为散列函数的目标是将不同的输入映射到不同的输出，而这里的散列函数未能实现这一目标。在实际应用中，这种特性可能导致哈希冲突，从而降低散列函数的性能。因此，在设计散列函数时，需要尽量避免这种情况下发生。

在这里插入图片描述

通义千问：

要证明这个性质，我们需要从形式上理解“串 x 可由串 y 通过其自身的字符置换排列导出”这句话的意思。这意味着对于每个字符 c 在 x 中的位置 i ，都有一个位置 j ，使得 c 在 y 中的位置就是 j 。也就是说，我们可以将 x 和 y 看作是从同一个字母表中选择字符组成的不同顺序的字符串。

现在我们来计算 h(x) 和 h(y) 。首先，将 x 和 y 转换为其按基数 $2^p$ 的表示形式，然后使用 h(k) = k mod m 计算它们的散列值。

由于 m=$2^p-1$ ，我们可以看到所有可能的字符位置都在模 m 的意义下等于它们自己。因此，无论我们将字符放置在何处，h(x) 都会保持不变。同样地，h(y) 也会保持不变。所以 h(x) == h(y) 成立。

然而，这种散列函数的一个缺点是它可能导致哈希碰撞，因为不同的输入可以产生相同的输出。这在很多场景下都是不希望出现的。例如，在数据库索引或查找表等需要唯一标识符的应用中，这种哈希函数可能会导致两个不同记录的键具有相同的哈希值，从而导致查找失败或者性能下降。

在这里插入图片描述

天工：

假设有两个字符串x和y，它们都可以通过y的字符置换排列导出。我们要证明它们具有相同的散列值h(x) 和 h(y)。

首先，我们可以通过将x和y表示为它们的基数为$2^p$的字符串，并将它们的每个字符进行置换，来构造两个新字符串x'和y'，它们分别是x和y的字符置换排列。

因为x和y可以通过y的字符置换排列导出，所以x'和y'是相同的。

接下来，我们可以使用除法散列法的另一种版本，其中h(k) = k mod m，m=$2^p-1$，k为按基数 $2^p$ 表示的字符串。

对于任意一个字符串k，它的散列值h(k)可以通过将它的每个字符的ASCII码值相加，然后对m取模得到。

因为x'和y'是相同的，它们的ASCII码值之和也是相同的。因此，它们的散列值h(x') 和 h(y')也是相同的。

因为h(x') 和 h(y')是相同的，所以x和y的散列值h(x) 和 h(y)也是相同的。

一个应用例子是密码学中的哈希函数。如果一个哈希函数具有这种特性，那么攻击者可以通过构造不同的字符串，但具有相同的散列值，来绕过哈希函数的安全性。因此，这种特性在哈希函数中是不希望出现的。

在这里插入图片描述

灵小智：

根据题意，假设字符串x和y是由相同的字符序列组成的，只是这些字符的顺序不一样。我们需要证明它们在使用除法散列法时具有相同的散列值。

首先，由于k是按基数 $2^p$ 表示的字符串，因此可以将k表示为 $k=b_{0}2^{{(p-1)}+b_{1}2}+...+b_{p-1}$，其中 $b_{i}$ 表示二进制串k的第i位。因此，可以得到：

$k \mod m = (b_{0}2^{{(p-1)}+b_{1}2}+...+b_{p-1}) \mod (2^p - 1)$

再利用模运算的分配律和余数定理，可以得到：

$k \mod m = ((b_{0} \mod (2^p - 1)) 2^{(p-1)} \mod (2^p - 1) + (b_{1} \mod (2^p - 1)) 2^{(p-2)} \mod (2^p - 1)+ ... +(b_{p-1} \mod (2^p - 1))) \mod (2^p - 1)$

注意到对于任意的n，有 $2^{n} \mod (2^n - 1) = 1$，因此可以得到：

$k \mod m = (b_{0} + b_{1} + ... + b_{p-1}) \mod (2^p - 1)$

也就是说，当两个字符串x和y具有相同的字符序列时，它们在除法散列法中产生的散列值相同，无论它们的字符顺序如何。

一个应用例子是密码学中的消息认证码（MAC）算法。MAC算法需要使用散列函数来生成消息的摘要，以确保消息的完整性和真实性。如果散列函数具有上述特性，则攻击者可以通过字符置换排列对原始消息进行修改而不影响其散列值，从而破坏MAC的安全性。因此，在设计MAC算法时，需要选择不具有这种特性的散列函数。

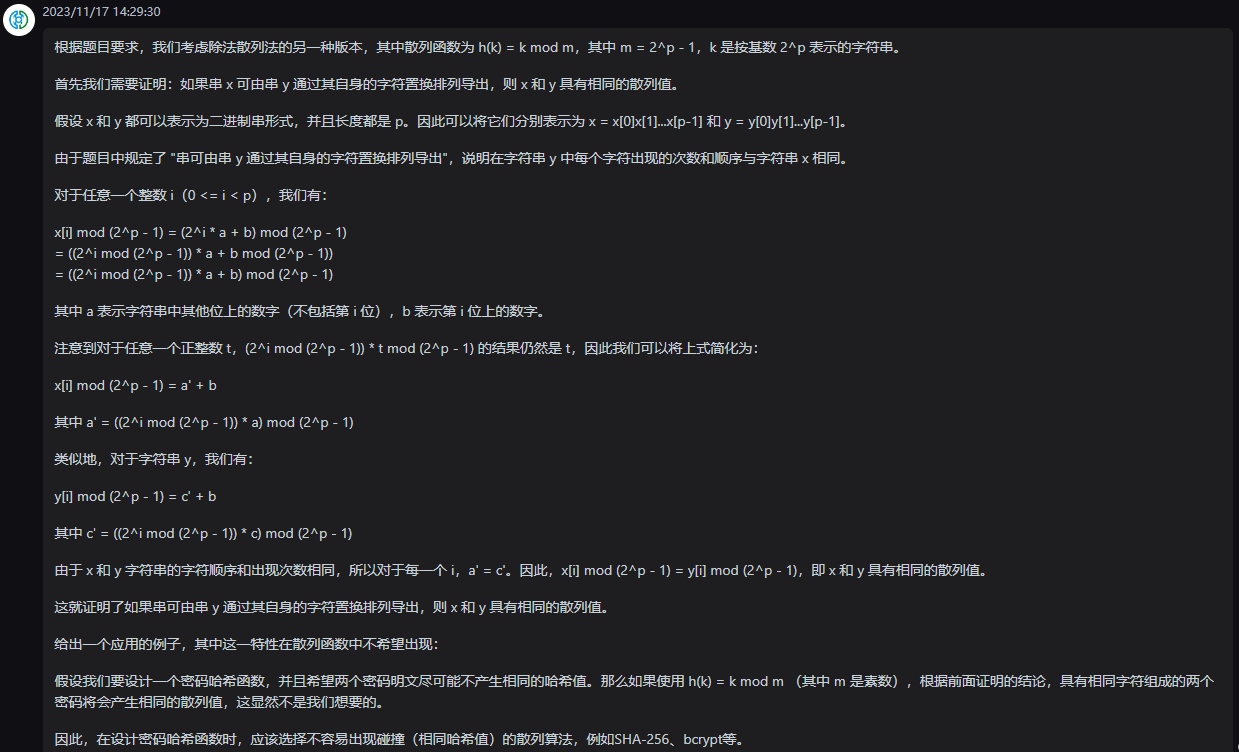
在这里插入图片描述