割点与桥
简介
割点:对于一个无向图,如果把一个点及与其相连的边删除后这个图分裂为两个及两个以上不连通的子图,那么这个点就是这个图的割点(又称割顶)。
割边:对于一个无向图,如果把一条边删除后这个图分裂为两个不连通的子图,那么这个点就是这个图的割边(又称桥)。
tarjan 求割点
定理:如果 \(x\) 为割点,那么在 \(x\) 的子节点只能通过 \(x\) 到达 \(x\) 的祖先节点。
证明:设 \(y\) 为 \(x\) 的子节点,\(z\) 为 \(x\) 的父节点,且有边 \(y→z\) 。
若去掉边 \(x→y\),图仍然连通,故 \(x\) 不是割点,与原条件矛盾,因此假设不成立。
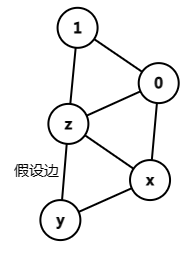
可以发现,如果一个节点不经过其父节点能到达的最小的时间戳如果大于其父节点的时间戳,那么它就满足只能通过其父节点到达其父节点的祖先节点。也就是说,它的父节点是割点。
这就是 tarjan 算法求割点的核心原理。
tarjan 求割点的流程:
-
求出每个节点时间戳 \(dfn_i\)(dfs 序)。
-
访问节点 \(x\)。
- 遍历 \(x\) 的每个子节点 \(y\)。
- 求出每个节点 \(y\) 不经过其父亲能到达的最小的时间戳,记为 \(low_y\)。
- \(y\) 没被访问过
先处理以 \(y\) 为起点的子图。
更新 \(low_x\),显然有 \(low_x=\min(low_x,low_y)\)。
如果 \(x\) 不是连通块的起始节点并且 \(low_x\ge dfn_y\),\(x\) 是一个割点。 - \(y\) 被访问过
有 \(low_x=\min(low_x,dfn_y)\)。
- \(y\) 没被访问过
- 如果 \(x\) 是当前连通块的起点并且与两个以上的节点相连,\(x\) 是一个割点。
代码
#include <bits/stdc++.h>
using namespace std;
int n, m, t, idx, cnt, v[1000005], h[1000005], ne[1000005], dfn[1000005], low[1000005];
bool vis[1000005], flag[1000005];
inline void add(int a, int b) {
v[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
inline void tarjan(int x, int F) {
vis[x] = 1;
low[x] = dfn[x] = ++t;
int child = 0;
for (int i = h[x]; ~i; i = ne[i]) {
int y = v[i];
if (!vis[y]) {
tarjan(y, x);
low[x] = min(low[x], low[y]);
if (!flag[x] && F != x && low[y] >= dfn[x])
flag[x] = 1, cnt++;
child++;
} else if (y != F)
low[x] = min(low[x], dfn[y]);
}
if (!flag[x] && x == F && child >= 2)
flag[x] = 1, cnt++;
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m--) {
int x, y;
cin >> x >> y;
add(x, y), add(y, x);
}
for (int i = 1; i <= n; i++) {
if (vis[i])
continue;
t = 0, tarjan(i, i);
}
cout << cnt << '\n';
for (int i = 1; i <= n; i++)
if (flag[i])
cout << i << ' ';
return 0;
}