AVL平衡树
1 什么是AVL平衡树
AVL是两个人的人名
Adelson-Velsky和Landis,两个人都是俄罗斯人,是两人在1962年的论文中首次提出,是最早的自平衡二分搜索树
什么是平衡二叉树?
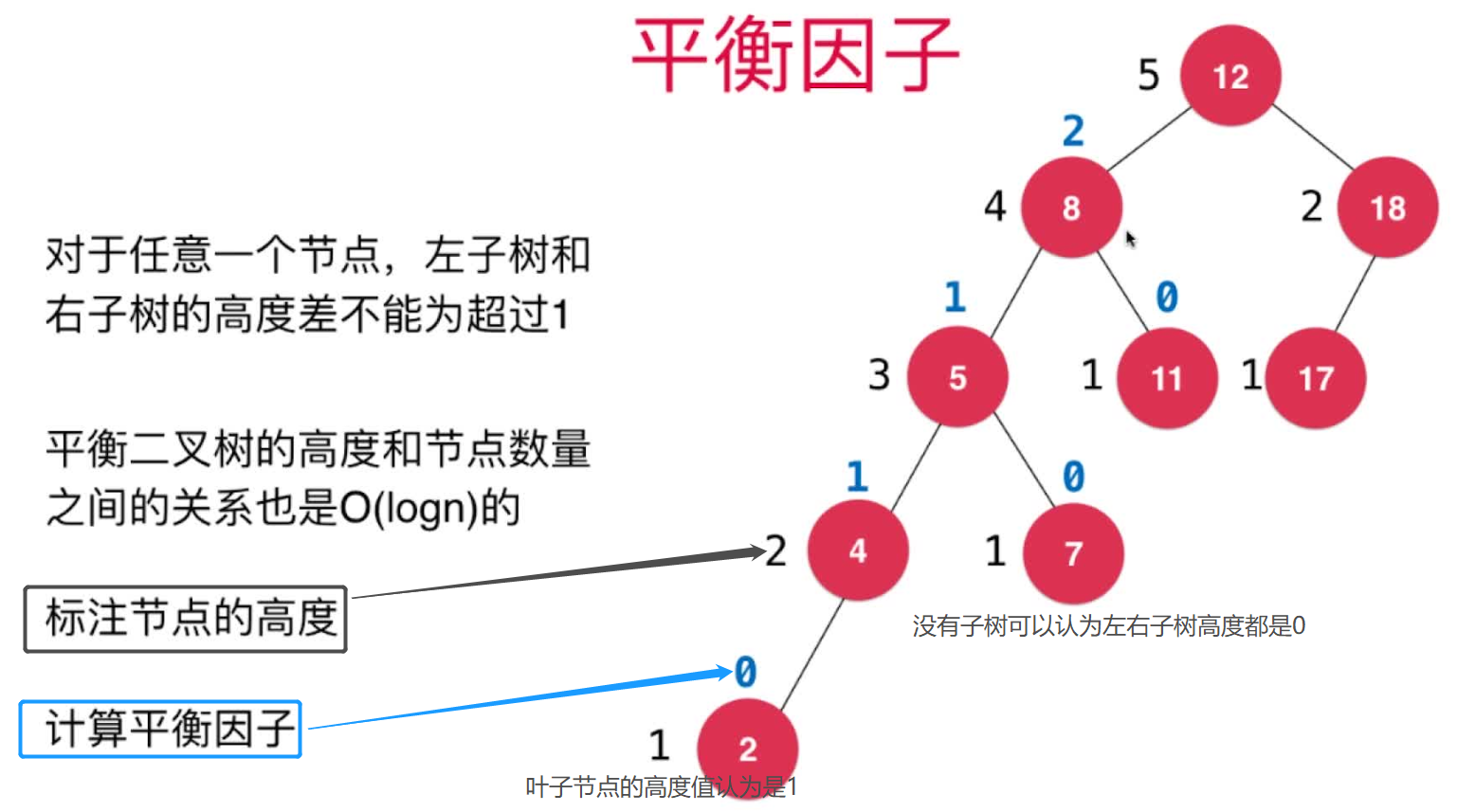
- 对任意一个节点,其左子树和右子树的高度差不能超过1
- 平衡二叉树的高度和节点数量之间的关系也是
O(logn)的 - 平衡二叉树某个节点的高度值=
max(左子树高度值,右子树高度值)+ 1。+1时因为父亲节点比子节点高一层。叶子节点的高度值认为是1,左右子树为空高度认为是0。在下图中用黑色表示
- 平衡二叉树某个节点的平衡因子=
左子树高度-右子树高度值,子树为空平衡因子认为是0在下图中用蓝色表示
平衡二叉树中"平衡"的含义
- 如果说一棵树是“平衡”的,就隐含着“这棵树的高度和节点数量成 log(n) 的关系”这样的信息,这也就是“平衡”的意义所在。
- 之所以要区分一棵树是否平衡,就是因为需要知道这棵树的操作复杂度是什么量级的。比如说“堆是一种平衡树”,实际上就是从操作复杂度说“堆的各种操作(insert、extract)的复杂度都是 O(logn)”。
2 结算节点的高度和平衡因子
只在add函数中更新节点高度height和节点平衡因子balance
/**
* 向以节点Node为根节点的二分搜索树树中添加新的键值对节点,递归实现
*
* @param node 二分搜索树的根节点
* @param key 要加入地节点的键
* @param val 要加入地节点的值
*/
private Node add(Node node, K key, V val) {
// 递归终止条件
if (node == null) {
// 只要碰到了为空的node,就一定要把我们的e作为节点添加到这里的,具体是作为左子树、右子树还是根节点到下面再进行设置
size++;
// 新加地节点刚开始都是叶子节点,所以Node的默认构造函数把height设置为1没问题,
return new Node(key, val);
}
// 递归组成逻辑
if (key.compareTo(node.key) < 0) {
// key小于根节点的key,往node的左子树继续遍历
node.left = add(node.left, key, val);
} else if (key.compareTo(node.key) > 0) {
// key大于根节点的key,往node的右子树继续遍历
node.right = add(node.right, key, val);
} else {
// 如果和遍历到的节点相等即key.compareTo(node.key)==0,则进行节点值更新
node.val = val;
}
// 更新当前节点和其往上节点的高度。平衡二叉树某个节点的高度值=max(左子树高度值,右子树高度值) + 1
// +1时因为父亲节点比子节点高一层。叶子节点的高度值认为是1,左右子树为空高度认为是0
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
// 获取节点的平衡因子,即node节点的左右子树的高度差的。子树为空平衡因子认为是0,即balance=左子树高度-右子树高度值
node.balance = getHeight(node.left) - getHeight(node.right);
if (Math.abs(node.balance) > 1) {
// 如果左右子树的高度差超过了1(平衡二叉树任何一个节点的左右子树高度差不大于1),说明不是平衡二叉树了
System.out.println("节点左右子树高度差超过1啦:" + node.balance);
}
// 当这个node是把key给new出来地就设置到子节点为空的上面去;如果不是new出来地相当于把已有的二分搜索树中的节点关系又设置一次
return node;
}
3 检查是否是二分搜索树BST和平衡二叉树AVL的要求
设计函数检查当前的二叉树是否满足如下特点:
判断是否是二分搜索树BST
二分搜索树BST的特点:
- 任意一个节点的左子树中的所有节点都小于这个节点
- 任意一个节点的右子树中的所有节点都大于这个节点
本节我们用地实际是"BST的中序遍历结果是升序的"这一个地6章得到的结论。
把遍历结果引用传值加入到keys列表中很巧妙
/**
* 判断当前的二叉树是否仍然是一棵二分搜索树BST
*/
public boolean isBST() {
List<K> keys = new ArrayList<>();
inOrder(root, keys);
// BST的中序遍历结果的一个特殊性质就是遍历结果是升序的
for (int i = 1; i < keys.size(); i++) {
if (keys.get(i - 1).compareTo(keys.get(i)) > 0) {
// 升序表明前面的节点应该小于后面的节点,当前面的节点大于后面的节点时,就说明二叉树不时BST的
return false;
}
}
return true;
}
/**
* 中序遍历以node作为根节点的二分搜索树,把遍历到的节点顺序加入到list中
*/
private void inOrder(Node node, List<K> keys) {
// 递归终止条件
if (node == null) {
// 遍历到null节点就返回上一层递归
return;
}
// 递归组成逻辑
// 2.遍历左子树
inOrder(node.left, keys);
// 1.访问当前节点。需要存储时可以放到list中
// 访问节点可以是打印也可以是存储到list中
// System.out.print(node.key + ":" + node.val + " ");
keys.add(node.key);
// 3.遍历右子树
inOrder(node.right, keys);
}
判断是否是平衡二叉树AVL
平衡二叉树AVL的特点:
- 满足BST的特点
- 对任意一个节点,其左子树和右子树的高度差不能超过1
/**
* 判断当前的二叉树是否是平衡二叉树,每个节点的平衡因子balance值的绝对值不能大于1
*/
public boolean isBalanced() {
return isBalanced(root);
}
/**
* 遍历当前二叉树的所有节点,看其balance值的绝对值是否大于1
*
* @param node 当前遍历到的子树的根节点
* @return 是否是平衡二叉树
*/
private boolean isBalanced(Node node) {
// 1.递归终止条件
if (node == null) {
// 递归到底了,空子树可以看做是平衡二叉树
return true;
}
if (Math.abs(node.balance) > 1) {
return false;
}
// 2.递归具体逻辑
// 左右子树递归进行遍历,两个都为平衡二叉树,整体的二叉树才是平衡二叉树
return isBalanced(node.left) && isBalanced(node.right);
}
本节相关代码
4 旋转操作的基本原理
新的节点加入会使得二叉树不再平衡(不满足上一届BST和AVL的性质),所以需要调整点使得二叉树重新平衡,这些操作下面会看到和旋转一样,一次我们称之为旋转操作
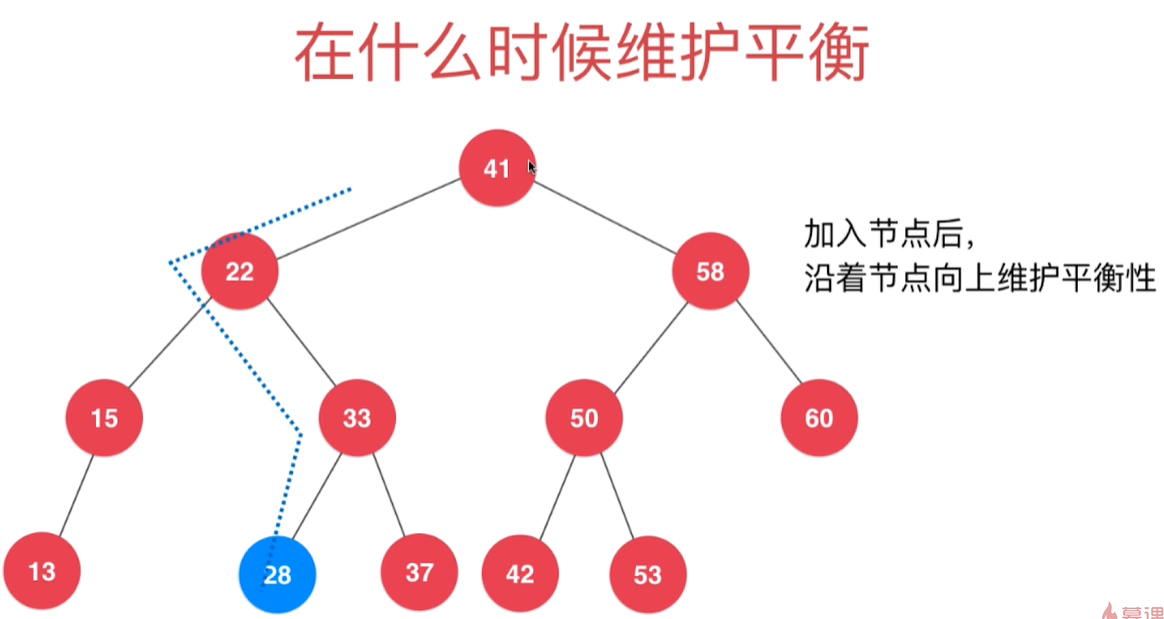
在什么是维护平衡(即旋转)?
加入新节点后,沿着新节点的插入的置向上维护平衡性
进行旋转的时机是在add中当更新节点高度和平衡因子后
// 更新当前节点和其往上节点的高度。平衡二叉树某个节点的高度值=max(左子树高度值,右子树高度值) + 1
// +1时因为父亲节点比子节点高一层。叶子节点的高度值认为是1,左右子树为空高度认为是0
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
// 获取节点的平衡因子,即node节点的左右子树的高度差的。子树为空平衡因子认为是0,即balance=左子树高度-右子树高度值
node.balance = getHeight(node.left) - getHeight(node.right);
// Todo:加入新节点后通过旋转使得二叉树重新平衡
加入新节点导致原二叉树失衡的例子
- 例子1
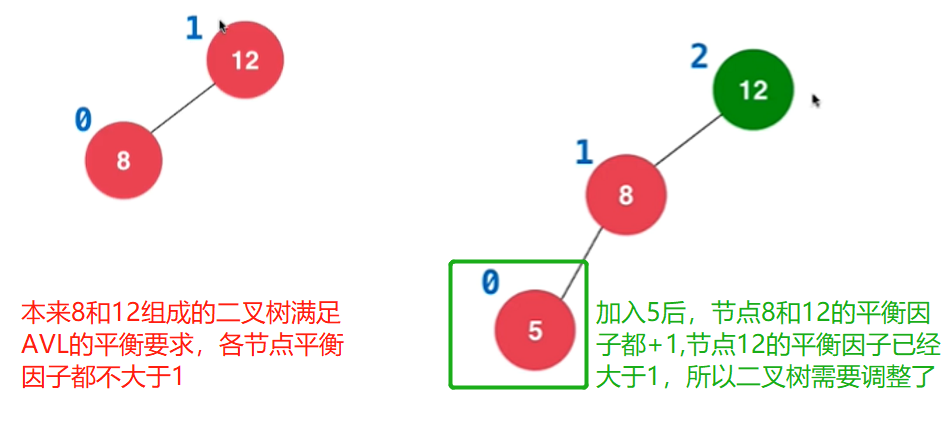
- 例子2
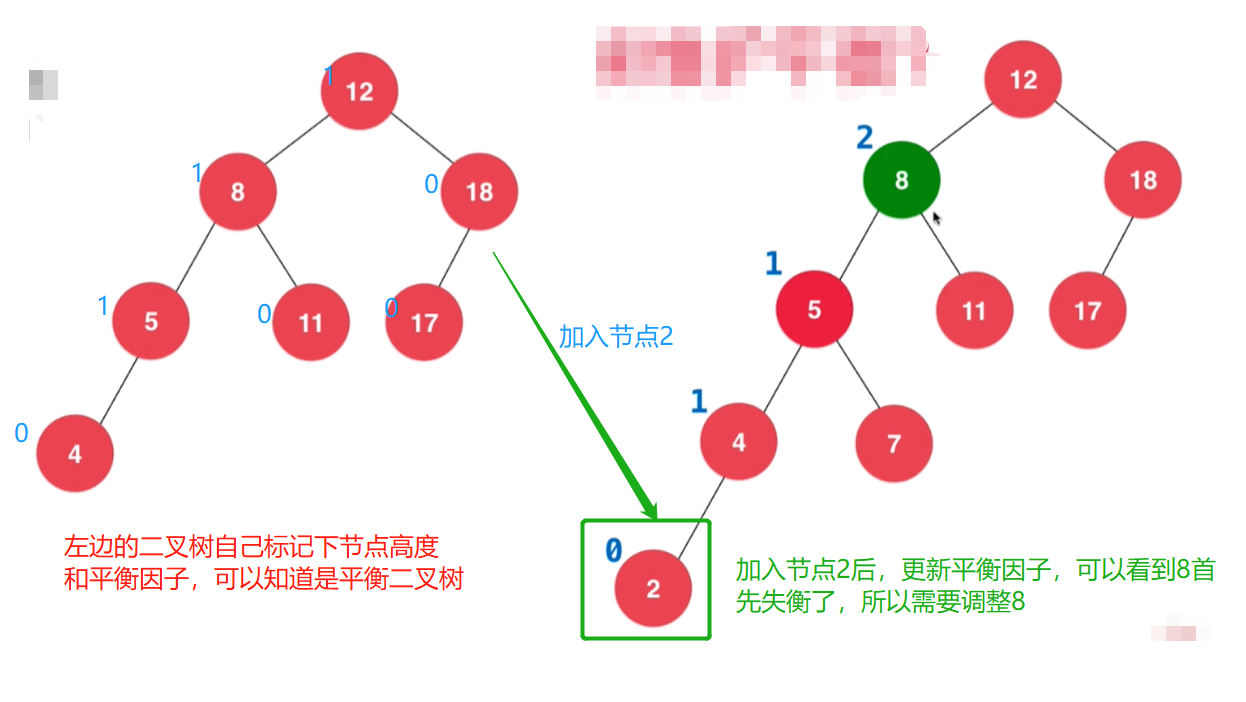
5~6 旋转的四种情形
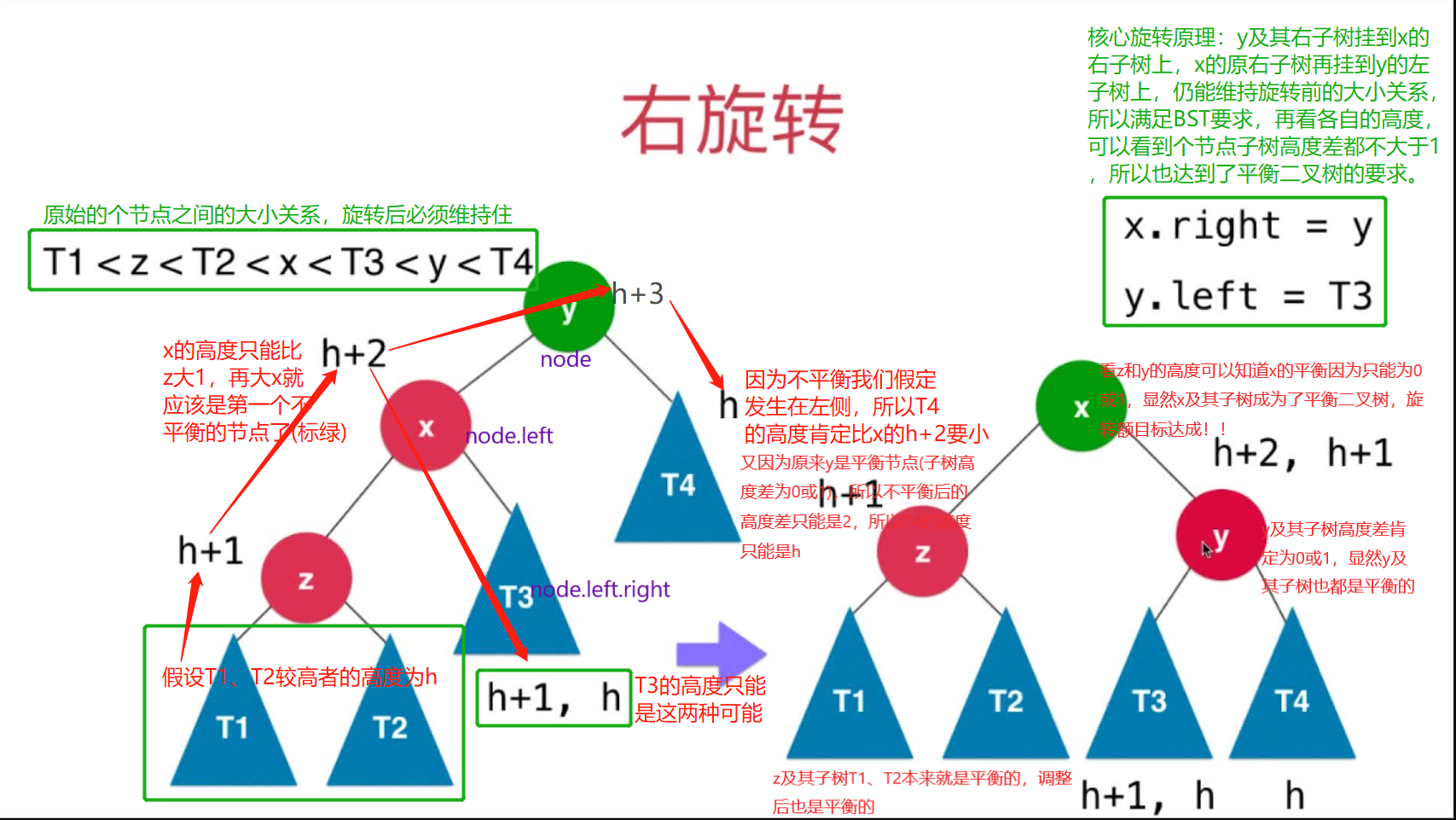
一、右旋转
不平衡是因为在
从下往上首个不平衡点(绿色标出)的左孩子的左侧新加入节点导致二叉树失衡,两个左,所以叫LL
/**
* 旋转情形1:不平衡发生在节点y左侧的左侧,需要进行右旋转
* 向右旋转的核心代码:x.right = y; y.left = T3
* // 对节点y进行向右旋转操作,返回旋转后新的根节点x
* // y x
* // / \ / \
* // x T4 向右旋转 (y) z y
* // / \ - - - - - - - -> / \ / \
* // z T3 T1 T2 T3 T4
* // / \
* // T1 T2
*
* @param y 二叉树中首个发现平衡因子大于1的节点
* @return 旋转后新的根节点x
*/
private Node rotateRight(Node y) {
Node x = y.left;
Node T3 = x.right;
// 右旋转的核心
x.right = y;
y.left = T3;
// 更新节点的Height,从上面注释的图可以看到z及其子树不用更新,T3和T4也不需要,只需要更新y和x即可
y.height = calHeight(y);
x.height = calHeight(x);
return x;
}
private Node add(Node node, K key, V val) {
......
// 旋转情形1:node左侧的左侧添加的节点导致node点不再平衡
if (balance > 1 && calBalance(node.left) >= 0) {
// 旋转后返回给上一层新的根节点,上面失衡的节点会继续按照旋转的流程使自己再次平衡,直到递归结束,整个二叉树也就再次平衡了
return rotateRight(node);
}
......
}
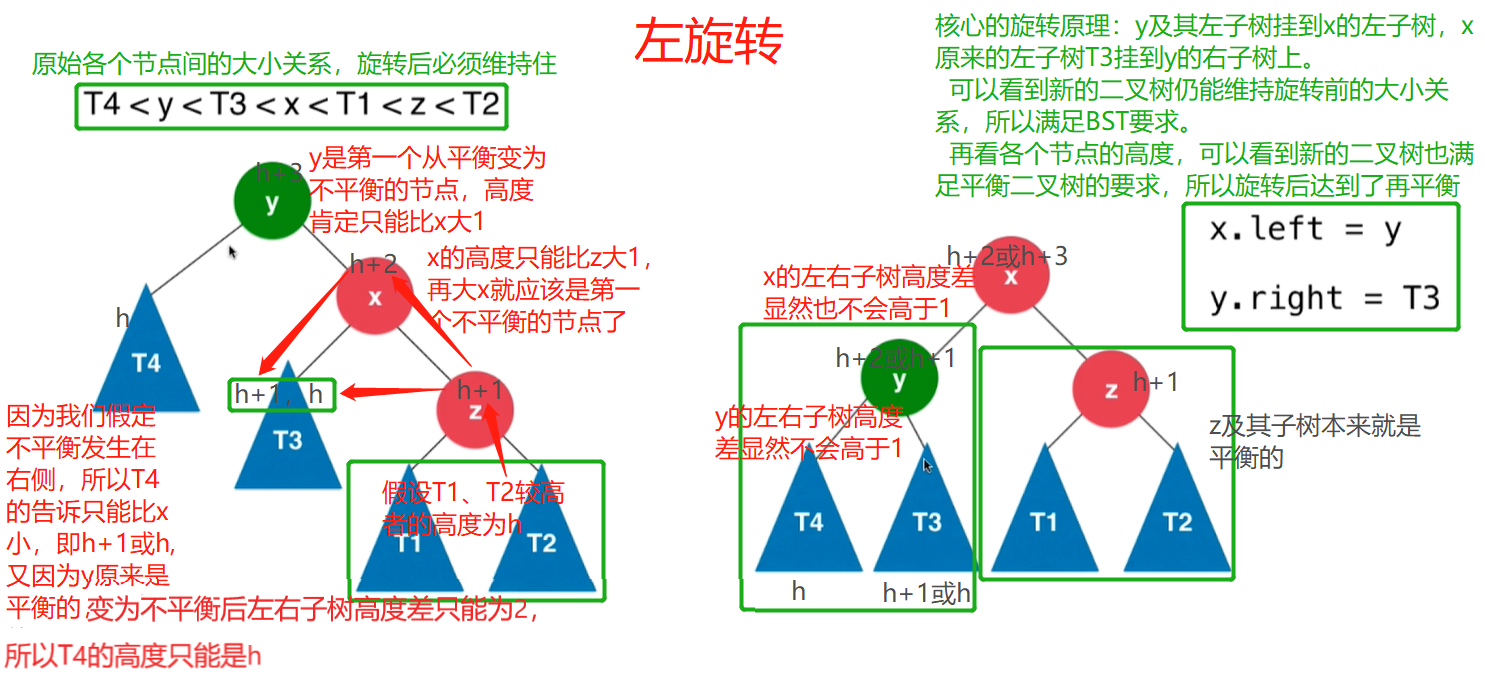
二、左旋转
不平衡是因为在
从下往上首个不平衡点(绿色标出)的右孩子的右侧新加入节点导致二叉树失衡,两个右,所以叫RR
/**
* 旋转情形2:不平衡发生在节点y右侧的右侧,需要进行左旋转
* 向右旋转的核心代码:x.left = y; y.right = T3
* // 对节点y进行向左旋转操作,返回旋转后新的根节点x
* // y x
* // / \ / \
* // T4 x 向左旋转 (y) y z
* // / \ - - - - - - - -> / \ / \
* // T3 z T4 T3 T1 T2
* // / \
* // T1 T2
*
* @param y 二叉树中首个发现平衡因子小于-1的节点
* @return 旋转后新的根节点x
*/
private Node rotateLeft(Node y) {
Node x = y.right;
Node T3 = x.left;
// 坐旋转过程
x.left = y;
y.right = T3;
// 更新height
y.height = calHeight(y);
x.height = calHeight(x);
return x;
}
private Node add(Node node, K key, V val) {
......
// 旋转情形2:node右侧的右侧添加的节点导致node点不再平衡
if (balance < -1 && calBalance(node.right) <= 0) {
// 旋转后返回给上一层新的根节点,上面失衡的节点会继续按照旋转的流程使自己再次平衡,直到递归结束,整个二叉树也就再次平衡了
return rotateLeft(node);
}
......
}
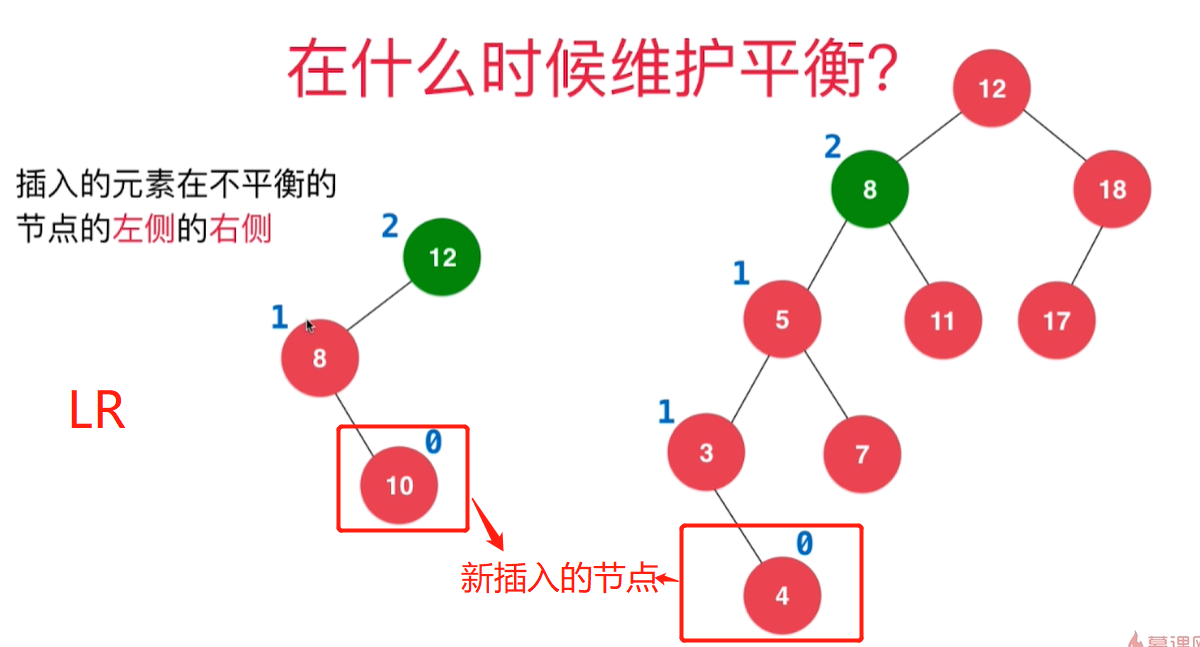
三.先左旋转再右旋转
不平衡是因为在
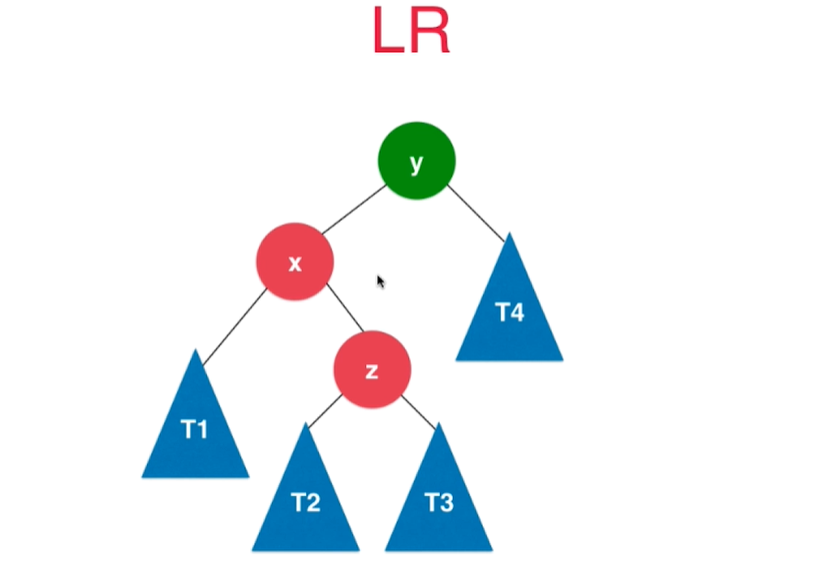
从下往上首个不平衡点(绿色标出)的左孩子的右侧新加入节点导致二叉树失衡,先左后右,所以叫LR
抽象模型如下图左边,不平衡是因为y的左孩子x的右侧
z及其子树中多了新的节点
这种情况的解决策略是: 先对x进行左旋转,把题目模型变成LL,然后再用LL的方法使得二叉树重新平衡即可
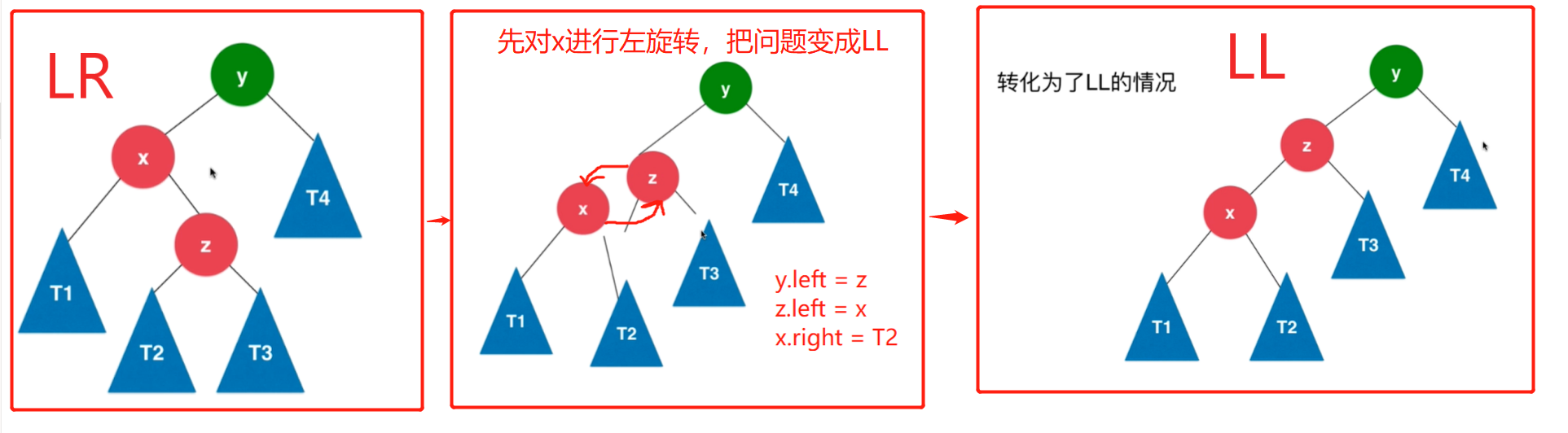
然后用LL的右旋转使得二叉树重新平衡。
综上:LR问题的解决方案是先左旋转然后右旋转。LR转LL是左旋转,LL转平衡是右旋转
// 旋转情形3:node左子树的右侧添加的节点导致node点不再平衡。先左后右所以叫LR
if (balance > 1 && calBalance(node.left) < 0) {
// 旋转后返回给上一层新的根节点,上面失衡的节点会继续按照旋转的流程使自己再次平衡,直到递归结束,整个二叉树也就再次平衡了
// 先对y的左孩子x执行一次左旋转,把问题转换成LL。node.left变成旋转后新的节点
node.left = rotateLeft(node.left);
// LL问题需要再对新的树执行一次右旋转
return rotateRight(node);
}
四.先右旋转再左旋转
不平衡是因为在
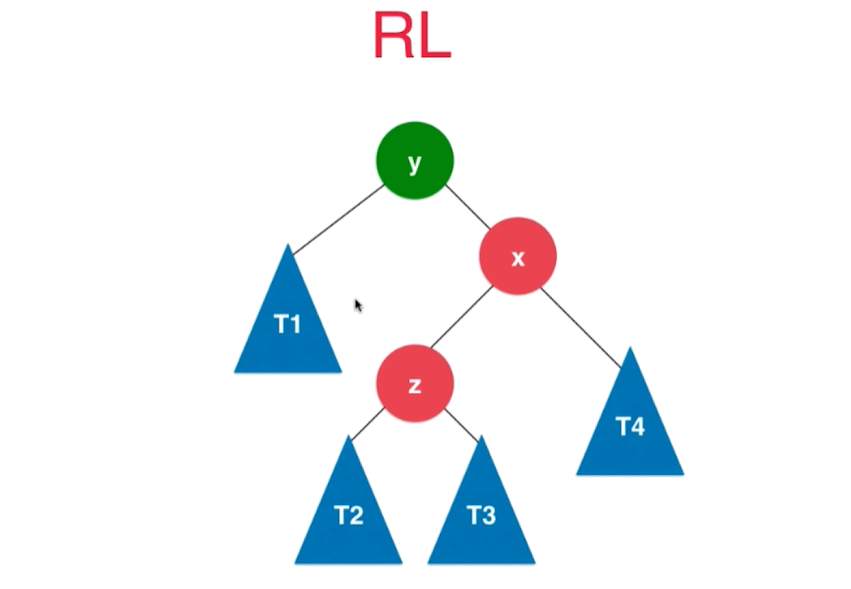
从下往上首个不平衡点(绿色标出)的右孩子的左侧新加入节点导致二叉树失衡,先右后左,所以叫RL
抽象模型如下图左边,不平衡是因为y的右孩子x的左侧
z及其子树中多了新的节点
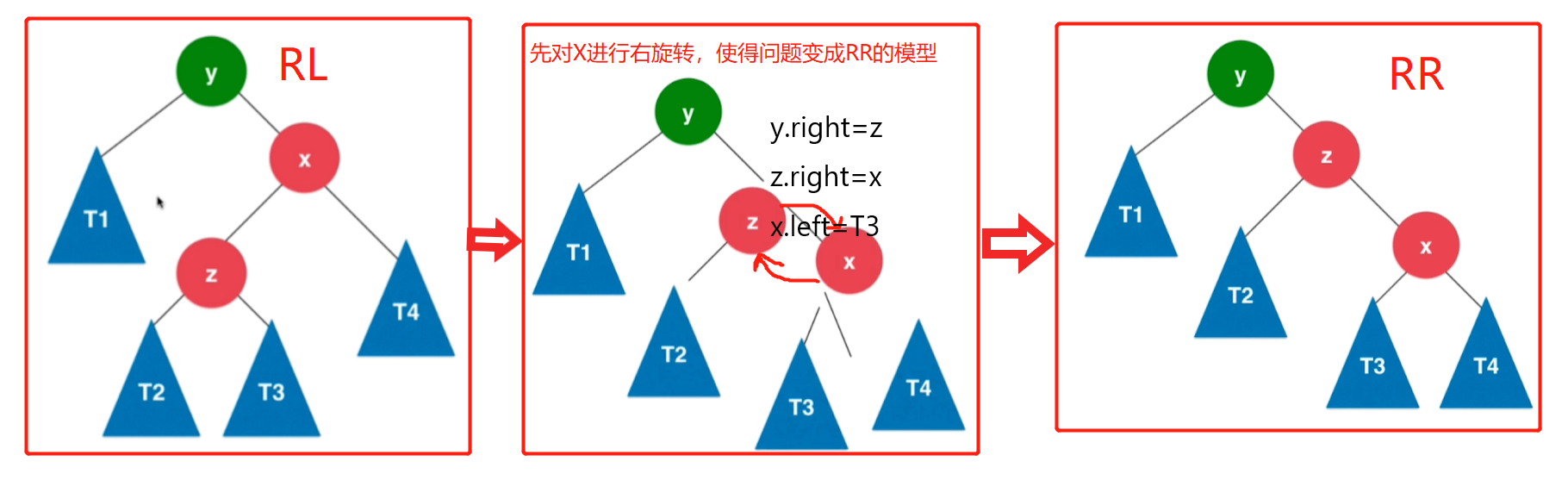
这种情况的解决策略是: 先对x进行右旋转,把题目模型变成RR,然后再用RR的方法使得二叉树重新平衡即可
然后用RR的右旋转使得二叉树重新平衡。
综上:RL问题的解决方案先右旋转然后左旋转。RL转RR是右旋转,RR转平衡是左旋转
// 旋转情形4:node右子树的左侧添加的节点导致node点不再平衡。先右后左所以叫RL
if (balance < -1 && calBalance(node.right) > 0) {
// 旋转后返回给上一层新的根节点,上面失衡的节点会继续按照旋转的流程使自己再次平衡,直到递归结束,整个二叉树也就再次平衡了
// 先对y的右孩子x执行一次右旋转,把问题转换成RR。node.right变成旋转后新的节点
node.right = rotateRight(node.right);
// RR问题需要再对新的树执行一次左旋转
return rotateLeft(node);
}
总结:对未经旋转的BST和经过旋转的BST(即AVL)进行了性能测试~最坏情况下(即输入有序)两者的性能能差上千倍
public class PerformanceTest {
public static void main(String[] args) {
System.out.println("Pride and Prejudice");
long startTime, endTime;
ArrayList<String> words = new ArrayList<>();
String filename = "src/main/java/Chapter07SetAndMap/Section1SetBasicAndBSTSet/pride-and-prejudice.txt";
if (FileOperation.readFile(filename, words)) {
// 排序后看看性能,这样最能测AVL的实现好不好。未经旋转的BST加入节点后整个BST会蜕化成一条链表,新加入的节点都要遍历整个BST才能找到自己的位置
// 旋转后的BST在加过节点后都会调整使得BST重新保持为平衡二叉树AVL,性能要比没旋转地高
Collections.sort(words);
// System.out.println("Total words: " + words.size());
// 1.未经旋转前的二分搜索树
startTime = System.nanoTime();
Chapter12AVLTree.Section3isBSTandisBalanced.BSTKV_AVL<String, Integer> avlBeforeRotate = new Chapter12AVLTree.Section3isBSTandisBalanced.BSTKV_AVL<>();
for (String word : words) {
if (avlBeforeRotate.contains(word)) {
// 之前存在地话就词频+1
avlBeforeRotate.set(word, avlBeforeRotate.get(word) + 1);
} else {
// 不存在就插入进去,词频初始化为1
avlBeforeRotate.add(word, 1);
}
}
// 查询操作时最消耗性能的,最能看出不平衡的BST和平衡的BST(即AVL)的性能差异
for (String word : words) {
avlBeforeRotate.contains(word);
}
endTime = System.nanoTime();
System.out.println("未经旋转前的BST耗时:" + (endTime - startTime) / 1000000000.0 + "s");
// 2.旋转后的二分搜索树
startTime = System.nanoTime();
Chapter12AVLTree.Section4to6RotateToReBalance.BSTKV_AVL<String, Integer> avlAfterRotate = new Chapter12AVLTree.Section4to6RotateToReBalance.BSTKV_AVL<>();
for (String word : words) {
if (avlAfterRotate.contains(word)) {
// 之前存在地话就词频+1
avlAfterRotate.set(word, avlAfterRotate.get(word) + 1);
} else {
// 不存在就插入进去,词频初始化为1
avlAfterRotate.add(word, 1);
}
}
// 查询操作时最消耗性能的,最能看出不平衡的BST和平衡的BST(即AVL)的性能差异
for (String word : words) {
avlAfterRotate.contains(word);
}
endTime = System.nanoTime();
System.out.println("经过旋转后的BST(即AVL)耗时:" + (endTime - startTime) / 1000000000.0 + "s");
// System.out.println("Total different words: " + avlAfterRotate.getSize());
// // 出现pride和prejudice单词的次数
// System.out.println("Frequency of PRIDE : " + avlBeforeRotate.get("pride"));
// System.out.println("Frequency of PREJUDICE : " + avlBeforeRotate.get("prejudice"));
// System.out.println("二叉树是否是二分搜索树BST:" + avlBeforeRotate.isBST());
// // 还没进行平衡处理,肯定是不平衡的
// System.out.println("二叉树是否是平衡二叉树:" + avlBeforeRotate.isBalanced());
}
}
}
/**
* Pride and Prejudice
* 未经旋转前的BST耗时:19.2616994s
* 经过旋转后的BST(即AVL)耗时:0.0535379s
*/
7 AVL节点的删除
在第6章BST中删除节点的基础上考虑到LL、RR、LR、RL四种旋转再平衡的情况即可,和添加节点时完全相同
/**
* 删除指定值的结点
*
* @param key 节点的键
*/
public V remove(K key) {
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.val;
}
return null;
}
/**
* 删除
*
* @param node 二分搜索树的根节点
* @param key 待删除节点的键
* @return 要挂载到当前节点父节点的子树
*/
private Node remove(Node node, K key) {
// 递归终止条件
if (node == null) {
return null;
}
// 递归组成逻辑
// 还没找到就接着往下找
Node retNode;
if (key.compareTo(node.key) < 0) {
// 要找的值比当前节点小,向左递归
node.left = remove(node.left, key);
retNode = node;
} else if (key.compareTo(node.key) > 0) {
// 要找的值比当前节点大,向右递归
node.right = remove(node.right, key);
retNode = node;
} else {
// node.key == key 找到相等的节点了,下面删除指定值的节点
if (node.left == null) {
Node rightNode = node.right;
// 释放引用
node.right = null;
size--;
// 左节点为空,把node的右子树挂接到node的父亲节点即可
retNode = rightNode;
} else if (node.right == null) {
Node leftNode = node.left;
// 释放引用
node.left = null;
size--;
// 右节点为空,把node的左子树挂接到node的父亲节点即可
retNode = leftNode;
} else {
// node的左右子树都不为空,就找node的右子树的最小值来代替node
Node minimumRight = minimum(node.right);
// 警告:下面两行代码一定不要颠倒,一定要先设置right再设置left,否则会出现迭代引用!
// 选出node右子树最小元素来代替node,那么右子树最小元素就要从原来位置删掉
minimumRight.right = removeMin(node.right);
// 替换当前节点node的左右子树
minimumRight.left = node.left;
// 释放node的引用
node.left = node.right = null;
// 返回给上一级来设置父节点
retNode = minimumRight;
}
}
// 删除前再进行一次平衡操作
return rotateToReBalance(retNode);
}
总结:经过上面的四种旋转和删除操作(remove、removeMin、removeMax),我们把节点旋转再平衡的操作封装成了如下的函数(核心是
rotateToReBalance())~方便节点增删时直接调用
/**
* 获取指定节点的高度值
*
* @param node 要查询高度的节点
* @return node节点的高度
*/
private int getHeight(Node node) {
if (node == null) {
// 空间点的高度值我们认为是0
return 0;
}
return node.height;
}
/**
* 计算节点的高度
* 节点的高度值= max(左子树高度值,右子树高度值) + 1
*
* @param node 当前高度
* @return 根据左右子树计算得到的高度
*/
private int calHeight(Node node) {
if (node == null) {
return 0;
}
// 不需要考虑node为null的情况,因为getHeight()已经考虑到了,node子节点为空直接返回0,不影响下面的计算
return Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
/**
* 计算节点node的平衡因子,即当前节点左子树高度减去右子树高度的差值
*
* @param node 当前节点
* @return 平衡因子
*/
private int calBalance(Node node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
/**
* 旋转情形1:不平衡发生在节点y左侧的左侧,需要进行右旋转
* 向右旋转的核心代码:x.right = y; y.left = T3
* // 对节点y进行向右旋转操作,返回旋转后新的根节点x
* // y x
* // / \ / \
* // x T4 向右旋转 (y) z y
* // / \ - - - - - - - -> / \ / \
* // z T3 T1 T2 T3 T4
* // / \
* // T1 T2
*
* @param y 二叉树中首个发现平衡因子大于1的节点
* @return 旋转后新的根节点x
*/
private Node rotateRight(Node y) {
Node x = y.left;
Node T3 = x.right;
// 右旋转的核心
x.right = y;
y.left = T3;
// 更新节点的Height,从上面注释的图可以看到z及其子树不用更新,T3和T4也不需要,只需要更新y和x即可
y.height = calHeight(y);
x.height = calHeight(x);
return x;
}
/**
* 旋转情形2:不平衡发生在节点y右侧的右侧,需要进行左旋转
* 向右旋转的核心代码:x.left = y; y.right = T3
* // 对节点y进行向左旋转操作,返回旋转后新的根节点x
* // y x
* // / \ / \
* // T4 x 向左旋转 (y) y z
* // / \ - - - - - - - -> / \ / \
* // T3 z T4 T3 T1 T2
* // / \
* // T1 T2
*
* @param y 二叉树中首个发现平衡因子小于-1的节点
* @return 旋转后新的根节点x
*/
private Node rotateLeft(Node y) {
Node x = y.right;
Node T3 = x.left;
// 坐旋转过程
x.left = y;
y.right = T3;
// 更新height
y.height = calHeight(y);
x.height = calHeight(x);
return x;
}
/**
* 根绝当前节点的平衡因子判断是否需要进行旋转
*
* @param node 当前节点
* @return 旋转后新的根节点
*/
private Node rotateToReBalance(Node node) {
if (node == null) {
return null;
}
// 更新节点的height,这个无比要做,要不会下面的平衡操作都是白搭~~!!!
// 更新当前节点和其往上节点的高度。平衡二叉树某个节点的高度值=max(左子树高度值,右子树高度值) + 1
// +1时因为父亲节点比子节点高一层。叶子节点的高度值认为是1,左右子树为空高度认为是0
node.height = calHeight(node);
// 获取节点的平衡因子,即node节点的左右子树的高度差的。子树为空平衡因子认为是0,即balance=左子树高度-右子树高度值
int balance = calBalance(node);
// 下面这3行可以打开用于观察旋转过程中平衡因子的变化
// if (Math.abs(balance) > 1) {
// System.out.println(balance);
// }
// 旋转情形1:node左子树的左侧添加的节点导致node点不再平衡。两个左所以叫LL
if (balance > 1 && calBalance(node.left) >= 0) {
// 旋转后返回给上一层新的根节点,上面失衡的节点会继续按照旋转的流程使自己再次平衡,直到递归结束,整个二叉树也就再次平衡了
return rotateRight(node);
}
// 旋转情形2:node右子树的右侧添加的节点导致node点不再平衡。两个右所以叫RR
if (balance < -1 && calBalance(node.right) <= 0) {
// 旋转后返回给上一层新的根节点,上面失衡的节点会继续按照旋转的流程使自己再次平衡,直到递归结束,整个二叉树也就再次平衡了
return rotateLeft(node);
}
// 旋转情形3:node左子树的右侧添加的节点导致node点不再平衡。先左后右所以叫LR
if (balance > 1 && calBalance(node.left) < 0) {
// 旋转后返回给上一层新的根节点,上面失衡的节点会继续按照旋转的流程使自己再次平衡,直到递归结束,整个二叉树也就再次平衡了
// 先对y的左孩子x执行一次左旋转,把问题转换成LL。node.left变成旋转后新的节点
node.left = rotateLeft(node.left);
// LL问题需要再对新的树执行一次右旋转
return rotateRight(node);
}
// 旋转情形4:node右子树的左侧添加的节点导致node点不再平衡。先右后左所以叫RL
if (balance < -1 && calBalance(node.right) > 0) {
// 旋转后返回给上一层新的根节点,上面失衡的节点会继续按照旋转的流程使自己再次平衡,直到递归结束,整个二叉树也就再次平衡了
// 先对y的右孩子x执行一次右旋转,把问题转换成RR。node.right变成旋转后新的节点
node.right = rotateRight(node.right);
// RR问题需要再对新的树执行一次左旋转
return rotateLeft(node);
}
// 不需要维护平衡,直接返回原节点
return node;
}
8 基于AVL树的集合Set和映射Map
集合Set
映射Map
AVL树的局限性
旋转次数过多,很影响性能。为了解决这个问题~诞生了第13章的红黑树