题目链接:大工程
先考虑只有一次查询,很显然我们可以暴力树上 dp 处理出答案。
对于每个节点而言,有:
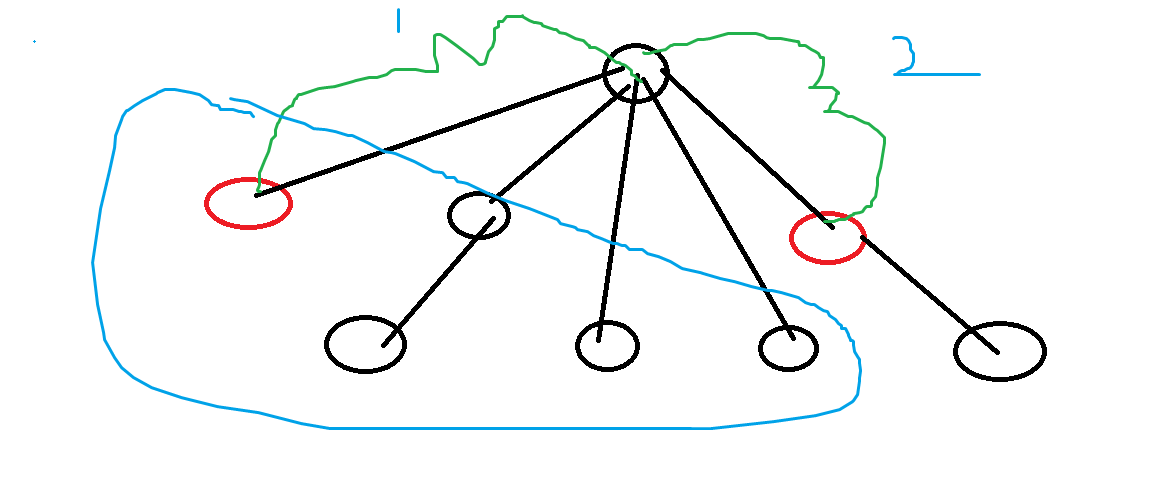
容易看出类似点分治逐个遍历子树计算前面一堆子树对后面子树的贡献思想,我们可以很容易的知道:
- 对于路径总和,显然多了一段新的贡献,这段贡献为当前关键点和前面点多的一段 \(2\) 号路线长。这段长很容易知道为 \(deep_{curr}-deep_{root}\)。而一共会多多少段这么多个长呢,我们可以用 \(k-size_{当前子树}\) 得到蓝色画圈区域的关键点数量,\(size\) 表示一棵树而言有多少个关键点。我们注意到,我们的树形 dp 常见的是从下往上 dp 的,即从叶子节点往上,因为这样而言,可以由若干子树 dp 情况更新根的 dp 信息。所以对于这棵正在更新的子树的所有关键点都会多一堆 \((k-siz_{当前子树})\times deepDiff\)。这样一来对于每一段的路径贡献我们可以很轻松的知道贡献增加:
翻译过来就是当前子树的所有关键点和前面子树的关键点配对,每一对最短路径都会多一段这段到根的距离,简单的贡献计算。
- 对于最大值和最小值路径长,我们可以考虑直接转移 dp 方程来做:
而知道这个信息以后,答案的最大值和最小值依旧可以考虑由以下情况构成:
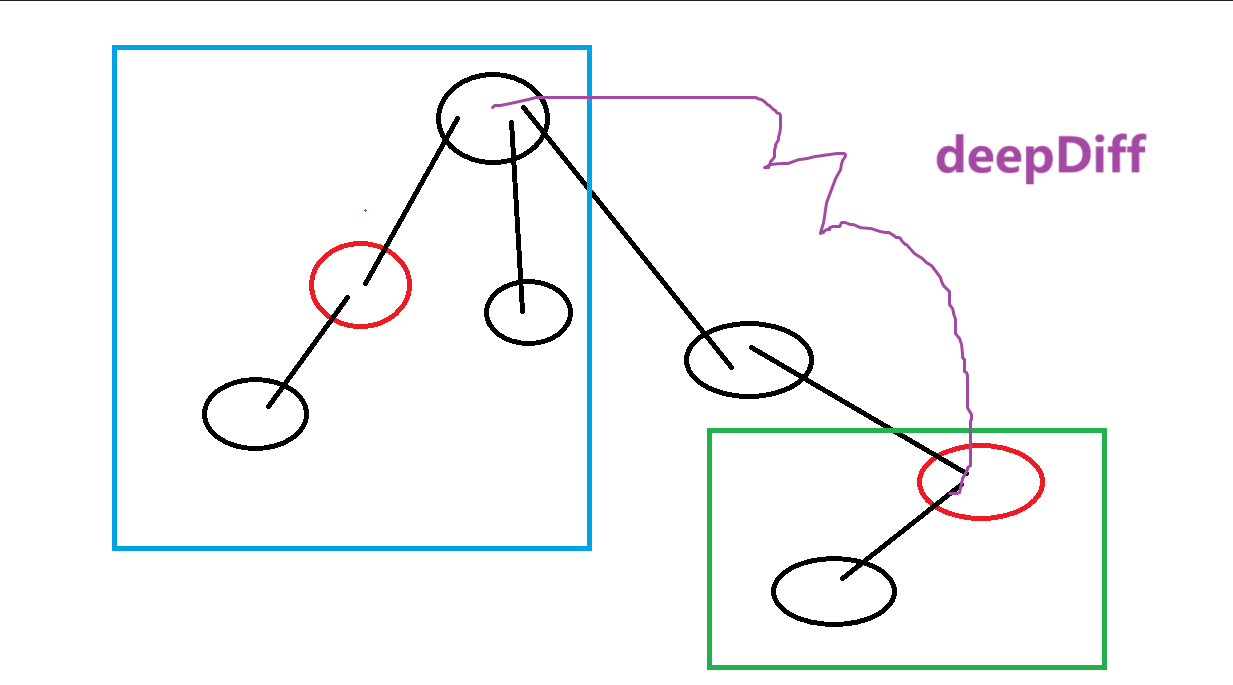
容易知道当前根是包括了还未更新当前子树的前面子树情况,所以可以直接由 \(dp_{根}+dp_{当前子树}+deepDiff\) 这三部分共同组成。
接下来解决多次查询的情况下,如何优化暴力 dp 的过程。很显然易见,我们容易观察到每对相邻关键点而言,它们所需要的信息仅仅是和 \(LCA\) 有关,作为中介点,而中间的路径都可以直接 \(deep\) 作差得到,所以很显然复杂度不对的原因,是 dp 的这棵树太大了,我们可以考虑使用虚树加速优化dp。其实也不是很高大上的东西,类似于缩点,我们把中间的点都给压缩掉,建立一棵只喊关键点和相邻关键点之间的 LCA 的虚树。为了方便从 \(1\) 号店,即根开始 dp,我们可以考虑无论如何都加入这个原树根节点在虚树当中。
建立虚树的大致方法
说一个借助 stl 库快速书写的方式,常数略大一点,但写起来很快。首先我们需要对关键点对进行排序,按照它们的 dfs 序排序,因为 dfs 越靠前的越容易作为父树,这样一来很容易拿到相邻关键对,然后我们对每个相邻点对算出 LCA 加入虚树待建点对当中,很显然,我们可以利用哈希集合进行去重。最后重新按 dfs 序以后就是利用笛卡尔建树的方式,利用栈建立,如果不是同一棵子树的点就弹出,是的话就建边。
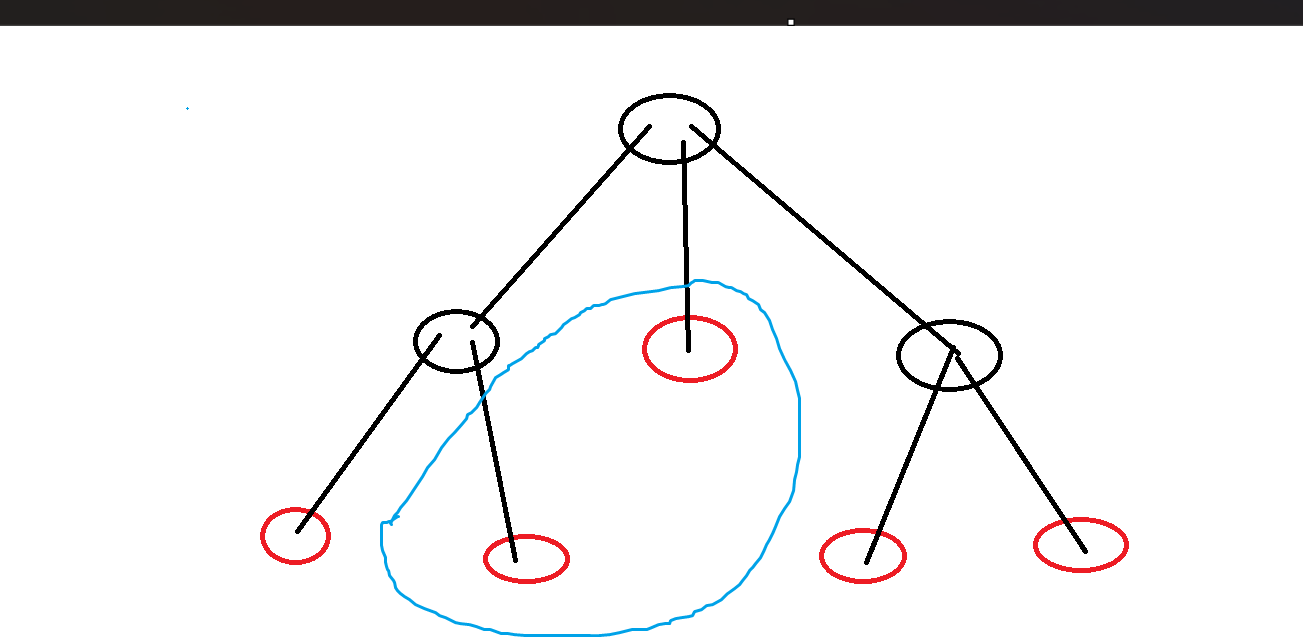
比如如图所示,蓝色部分就是不在同一棵子树的一对点,它们不需要建边。
好写的建虚树代码
#define all(v) v.begin(),v.end()
vector<int> node; //待建虚树的关键点
vector<int> vir[N]; //虚树
//后者在不在前者的子树中
inline bool isSame(const int pre, const int last)
{
return s[pre] <= s[last] and e[last] <= e[pre];
}
inline void buildVir()
{
//越前面的越容易当父树
auto cmp = [&](const int x, const int y)
{
return s[x] < s[y];
};
sort(all(node), cmp);
unordered_set need(all(node)); //待建点
forn(i, 1, node.size()-1)need.insert(LCA(node[i - 1], node[i])); //加入两两相邻关键点的LCA
node = vector(all(need));
sort(all(node), cmp); //得到最终虚树点
stack<int> st; //类似笛卡尔树建树
for (const auto curr : node)
{
while (!st.empty() and !isSame(st.top(), curr))st.pop(); //不是同一棵子树弹出
if (!st.empty())vir[st.top()].push_back(curr);
st.push(curr);
}
}
最后的细节
我们需要预处理 dfs 序和 求 LCA 的一些东西,这里由于不怎么用到修改,所以可以考虑用倍增就够了,最后我们注意每次建完虚树跑完 dp 以后记得清空虚树信息和原来 dp 信息即可。这样一来每次 dp 的点对最多为 \(2k\) 级别。而题目所说的 \(k\) 总和不超过 \(2n\),那么很显然这些所有的 \(dp\) 总复杂度仅仅只是 \(O(n)\) 级别。具体实现可见代码注释。
参照代码
#include <bits/stdc++.h>
//#pragma GCC optimize("Ofast,unroll-loops")
#define isPbdsFile
#ifdef isPbdsFile
#include <bits/extc++.h>
#else
#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>
#endif
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
template <typename T>
int disc(T* a, int n)
{
return unique(a + 1, a + n + 1) - (a + 1);
}
template <typename T>
T lowBit(T x)
{
return x & -x;
}
template <typename T>
T Rand(T l, T r)
{
static mt19937 Rand(time(nullptr));
uniform_int_distribution<T> dis(l, r);
return dis(Rand);
}
template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
return (a % b + b) % b;
}
template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
a %= c;
T1 ans = 1;
for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
return modt(ans, c);
}
template <typename T>
void read(T& x)
{
x = 0;
T sign = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')sign = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
x *= sign;
}
template <typename T, typename... U>
void read(T& x, U&... y)
{
read(x);
read(y...);
}
template <typename T>
void write(T x)
{
if (typeid(x) == typeid(char))return;
if (x < 0)x = -x, putchar('-');
if (x > 9)write(x / 10);
putchar(x % 10 ^ 48);
}
template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
write(x), putchar(c);
write(c, y...);
}
template <typename T11, typename T22, typename T33>
struct T3
{
T11 one;
T22 tow;
T33 three;
bool operator<(const T3 other) const
{
if (one == other.one)
{
if (tow == other.tow)return three < other.three;
return tow < other.tow;
}
return one < other.one;
}
T3() { one = tow = three = 0; }
T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
{
}
};
template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
if (x < y)x = y;
}
template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
if (x > y)x = y;
}
constexpr int N = 1e6 + 10;
vector<int> child[N];
constexpr int T = ceil(log2(N));
int deep[N], fa[N][T + 1];
int siz[N]; //虚树子树的关键点数量
bool vis[N]; //是否是关键点
int minDp[N], maxDp[N]; //虚树最小值和最大值对应的dp转移方程
ll ansSum, ansMax, ansMin; //三个答案
int s[N], e[N], cnt;
constexpr int INF = 1e9 + 7;
//预处理dfs序和树上倍增数组
inline void dfs(const int curr, const int pa)
{
deep[curr] = deep[pa] + 1;
fa[curr][0] = pa;
forn(i, 1, T)fa[curr][i] = fa[fa[curr][i - 1]][i - 1];
s[curr] = ++cnt;
for (const auto nxt : child[curr])if (nxt != pa)dfs(nxt, curr);
e[curr] = cnt;
}
//倍增求LCA
inline int LCA(int x, int y)
{
if (deep[x] < deep[y])swap(x, y);
forv(i, T, 0)if (deep[fa[x][i]] >= deep[y])x = fa[x][i];
if (x == y)return x;
forv(i, T, 0)if (fa[x][i] != fa[y][i])x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
vector<int> node; //待建虚树的关键点
vector<int> vir[N]; //虚树
//后者在不在前者的子树中
inline bool isSame(const int pre, const int last)
{
return s[pre] <= s[last] and e[last] <= e[pre];
}
inline void buildVir()
{
//越前面的越容易当父树
auto cmp = [&](const int x, const int y)
{
return s[x] < s[y];
};
sort(all(node), cmp);
unordered_set need(all(node)); //待建点
forn(i, 1, node.size()-1)need.insert(LCA(node[i - 1], node[i])); //加入两两相邻关键点的LCA
node = vector(all(need));
sort(all(node), cmp); //得到最终虚树点
stack<int> st; //类似笛卡尔树建树
for (const auto curr : node)
{
while (!st.empty() and !isSame(st.top(), curr))st.pop(); //不是同一棵子树弹出
if (!st.empty())vir[st.top()].push_back(curr);
st.push(curr);
}
}
ll k; //关键点对
//虚树上dp
inline void dp(const int curr)
{
siz[curr] = vis[curr]; //关键点数量就+1
minDp[curr] = vis[curr] ? 0 : INF; //初始化dp,关键点就是最小的
maxDp[curr] = 0; //初始化,关键点到自身的路径长也为0,不影响最大值
for (const auto nxt : vir[curr])
{
dp(nxt); //从叶子节点开始更新信息
int dist = deep[nxt] - deep[curr];
ansSum += (k - siz[nxt]) * siz[nxt] * dist; //每个点跟前面已经更改的子树多一段到LCA的贡献
if (siz[curr]) //前面部分有无出现关键点
{
uMin(ansMin, minDp[curr] + minDp[nxt] + dist);
uMax(ansMax, maxDp[curr] + maxDp[nxt] + dist);
}
//常规更新树形dp,不过注意这里不是长度为1而是两个点之间的距离
uMin(minDp[curr], minDp[nxt] + dist);
uMax(maxDp[curr], maxDp[nxt] + dist);
siz[curr] += siz[nxt]; //关键对累计
}
vis[curr] = false; //更新完关键点dp,清零用于下次dp使用
}
int n, m, x;
inline void solve()
{
cin >> n;
forn(i, 1, n-1)
{
int u, v;
cin >> u >> v;
child[u].push_back(v);
child[v].push_back(u);
}
dfs(1, 0);
cin >> m;
while (m--)
{
cin >> k;
forn(i, 1, k)cin >> x, vis[x] = true, node.push_back(x);
if (!vis[1])node.push_back(1); //1如果不在要加入,方便从1开始dp
buildVir();
ansSum = ansMax = 0, ansMin = INF;
dp(1);
cout << ansSum << " " << ansMin << " " << ansMax << endl;
for (const auto v : node)vir[v].clear();
node.clear();
}
}
signed int main()
{
Spider
//------------------------------------------------------
int test = 1;
// read(test);
// cin >> test;
forn(i, 1, test)solve();
// while (cin >> n, n)solve();
// while (cin >> test)solve();
}