2023.12随笔
Problem A: 括号
从前往后扫,当扫到 \(s_i\) 且 \(s_i=')'\) 时,统计前 \(i-1\) 个字符与 \(s\) 相同,第 \(i\) 个字符与 \(s\) 不同的字符串 \(t\) 的个数。
设 \([1,i]\) 中 \(s\) 有 \(k\) 个尚未匹配的 \('('\) ,再加上 \(s_i\) 本身,说明 \(t\) 在 \([i+1,n]\) 中有 \(k+1\) 个多余的 \(')'\) 。每出现一个 \(')'\) 表示向右走,每出现一个 \('('\) 表示向上走,那么问题转化为:从 \((0,k+1)\) 走到 \((\frac{k+1+m}{2},\frac{k+1+m}{2})\) ,且路径一直在 \(y=x-1\) 上方(左括号数量一直 \(\ge\) 右括号数量)的方案数。
这个问题有一个经典做法:一旦路径与 \(y=x-1\) 有交点,就把路径在第一个交点以后的部分对称一下,可以发现:所有不合法的路径,与所有从起点到终点的对称点的路径一一对应。因此只需要找到终点的对称点 \((\frac{k+m+3}{2},\frac{k+m-1}{2})\) ,方案数就是:
Problem A: 歌唱盒与猫射线
首先求出 \(1\to 1\sim n\) 的最短路,然后只保留最短路经过的边,这样会形成一个 \(DAG\) 。
然后发现,满足题意的充要条件是除了 \(1\) 节点,每个节点都有至少两条入边。因此,只需要给入度为 \(1\) 的点加一条入边即可。设 \(dis[i]\) 表示 \(1\to i\) 的最短路长度,那么加入 \(x\to y\) 的边的边权就是 \(dis[y]-dis[x]\) 。
考虑将点以 \(dis\) 为关键字从小到大排序,遍历的时候维护 \(w\) 值最小点 \(f1\) 和次小点 \(f2\) 。对于只有一个入边的点 \(x\),设那个入点为 \(y\) ,如果 \(y=f1\) ,就连 \(f2\to x\) ,否则连 \(f1\to x\)
还有一个细节,题目中要求边权为正整数,所以要注意不能出现 \(dis[x]=dis[y]\) 的情况。所以 \(f1,f2\) 只统计 \(dis\) 值严格小于当前的点。
Problem C: Retribution
有一个很厉害的性质:对于一个点,能到达这个点的点集是一个矩形。
证明很简单,如果点集的边界有拐弯的地方,那么处在拐弯处,边界外的点就有至少两种方式进入边界,那么它就能到达指定点,那么边界就可以扩。
接下来,如果点 \((i,j)\) 能到点 \((x,y)\) ,那么就连一条 \((i,j)\to(x,y)\) 的边。然后进行缩点+拓扑排序,这样就能得到每个点对应的矩形。询问时就看起点有没有在终点的矩形内即可。
Problem C: 多米诺
对题解的补充:
为什么相邻两个障碍之间划分边界的方案数是 \(C_{x+y}^x-C_{x+y-2}^{x-1}\)
首先发现,每一个方案都可以看成点 \(A\) 走到点 \(B\) 的一条路径:
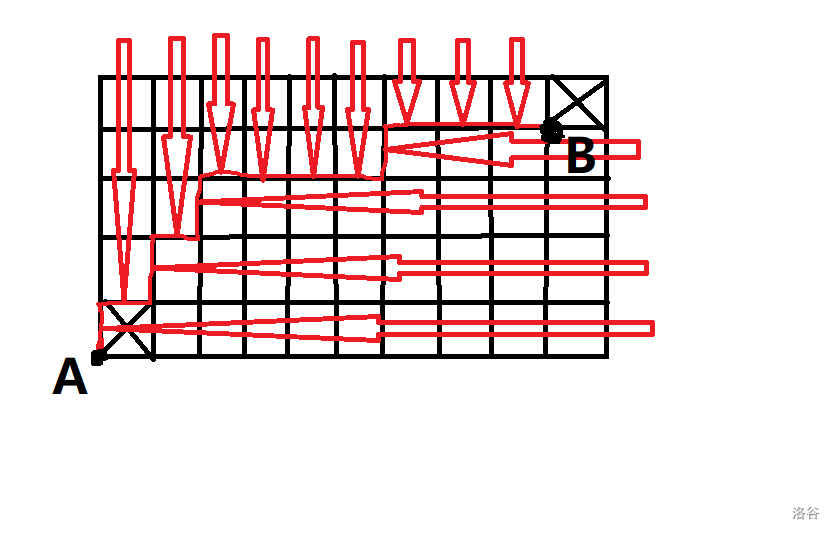
那么方案数应该是 \(C_{x+y}^{x}\) 。但是,我们发现,由于左下角存在障碍,所以以下两种情况实际上是一种,而计数的时候都算上了。

所以我们要减去从红点到 \(B\) 点的方案,即 \(C_{x+y-2}^{x-2}\) 。所以最终方案数为 \(C_{x+y}^x-C_{x+y-2}^{x-2}\)
CF1322E
中位数问题有一个很经典的套路:将 \(\ge x\) 的数看成 \(1\) ,\(<x\) 的数看成 \(0\) ,转化为 \(01\) 问题。
对于此题,首先考虑只有数字 \(0,1\) 的情况。首先,每次迭代时,只有每个极长,且长度 \(\ge3\) 的 \(01\) 交错段会发生改变。手膜一下可知,设 \([l,r]\) 是满足上述条件的段,那么经过 \(\lfloor\frac{r-l}{2}\rfloor\) 次操作以后,这个段就不再改变;每个数最终会变成什么遵循如下规律:
如果 \(r-l+1\) 为偶数,那么前一半与 \(a_l\) 相同,后一半与 \(a_r\) 相同;
如果 \(r-l+1\) 为奇数,那么 \([l,r]\) 的数最终都和 \(a_l\) 相同(此时\(a_l=a_r\))(其实可以和上一条合并)
接下来考虑一般的情况。首先设定 \(x\) 为所有数的最小值,将 \(>x\) 的数看成 \(0\) ,\(\le x\) 的数看成 \(1\) ,然后 \(x\) 不断自增,直到成为最大值。\(x\) 每 \(+1\) ,就是某些数从 \(0\) 变成 \(1\) 的过程,需要更改的段均摊下来是 \(O(1)\) 的,所以可以用 \(set\) 实时维护段的变化。知道所有时刻段长的最大值,就能知道操作次数。
还要求出最终序列是什么。我们可以新开一个 \(set\) ,里面存最终数值还不确定的位置。设位置 \(p\) 被更新了,找出所有更新完后,左端点或右端点为 \(1\) 的段,然后在新开的 \(set\) 里面找出这些段里不确定的数,把这些数的最终值更新成 \(x\) 。意思是说, \(set\) 里面原本不确定的数,是 \(>x_{las}\) 的,现在限制成了 \(\le x\) ,自然需要更新成 \(x\) 。
void update1(int l,int r,int w){//更新答案二
auto it=s1.lower_bound(l);//s1存了最终数值还不确定的位置
int t;
while(it!=s1.end()&&(*it)<=r){
t=(*it);
ans[t]=w;
++it;
s1.erase(t);
}
}
void update(int x,int w){
int l,r;auto it=s.lower_bound(x);
r=(*it);l=(*(--it))+1;
len=max(len,(r-l)>>1);//更新答案一
if(vis[l])
update1(l,(l+r)>>1,w);
if(vis[r])
update1(((l+r)>>1)+1,r,w);
}
void ins(int x){
if(x>1&&!vis[x-1])
s.erase(x-1);//s存了每个段的右端点
else
s.insert(x-1);
if(x<n&&!vis[x+1])
s.erase(x);
else
s.insert(x);
vis[x]=1;//vis表示当前是否为1
}
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;++i)
scanf("%lld",&a[i]),b[i]=a[i];
sort(b+1,b+n+1);
int cnt=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;++i)
a[i]=lower_bound(b+1,b+cnt+1,a[i])-b;
s.insert(0);
for(int i=1;i<=n;++i)
s.insert(i),s1.insert(i),c[a[i]].push_back(i);
for(int i=1;i<=cnt;++i){
for(auto j:c[i])
ins(j);
for(auto j:c[i]){
update(j,i);
if(j>1) update(j-1,i);
if(j<n) update(j+1,i);
}
}
printf("%lld\n",len);
for(int i=1;i<=n;++i)
printf("%lld ",b[ans[i]]);
fclose(stdin);fclose(stdout);
return 0;
}
Problem C: 三色球
这是一道交互题。
首先考虑只有两种颜色的况。显然可以问两次,第一次问 \((1,2),(3,4)...\) ,第二次问 \((2,3),(4,5)...\) ,这样就知道了任意 \((i,i+1)\) 之间是否相同了。然后从前往后扫,就能确定每个位置的颜色。
再考虑三种颜色的情况。上述操作实际上将序列划分成了若干段,段内颜色相同,相邻段颜色不同。设这些段分别是 \(f_1,f_2,f_3,f_4...,f_k(k\le n)\) ,那么再询问两次,第一次问 \((f_1,f_3),(f_2,f_4),(f_5,f_7),(f_6,f_8)...\) ,第二次问 \((f_3,f_5),(f_4,f_6),(f_7,f_9),(f_8,f_{10})...\) ,这样就知道任意 \((f_i,f_{i-2})\) 间是否相同了。又知道相邻段不同,所以钦定 \(f_1=1,f_2=2\) ,就能往后递推求得所有段的颜色。
Problem C: 黑鸭的字符串
首先考虑没有 \(?\) 怎么做。
首先钦定对于连续的一段 \(0\) ,每次删只删除末尾;对于连续的一段 \(1\) ,每次只删除开头,同时在字符窜开头补 \(0\) 。末尾补 \(1\) 。这样相当于每次删 \(01\) 中的一个。此外,在相邻字符串之间插板,每次删 \(01\) 时,记录中间的插板的删除时间,这样形成一个长度为 \(n+1\) 的排列。
这个排列和方案一一对应。根据删除规则,对于 \(0\) ,它右边的板会更早删除;对于 \(1\) ,它左边的板会更早删除,因此对于一个排列,可以通过。因此,对于一个板,比较它相邻的板的删除时间可以得到是删 \(0\) 还是删 \(1\) ,从而与方案一一对应。而对于一个方案,显然可以直接根据上述规则构造一个排列。
于是将 \(0\) 看成 \(<\) ,\(1\) 看成 \(>\) ,\(?\) 看成没有限制,问题转化成 LOJ575 不等关系 。