题目链接:[集训队互测 2018] 完美的队列
神仙数据结构题,看了很多题解才搞懂。在做此题之前,最好对分块很熟悉,对各类标记非常熟练。考虑题意说的种类是相对于全局的。我们可以考虑局部影响对全局影响。
人为规定:在第 \(m+1\) 时刻,无论队列中还有无元素,我们都把所有队列清空,便于后续的描述
放逐单点,我们考虑将每个 \([l,r]\) 的影响排成一列,观察:
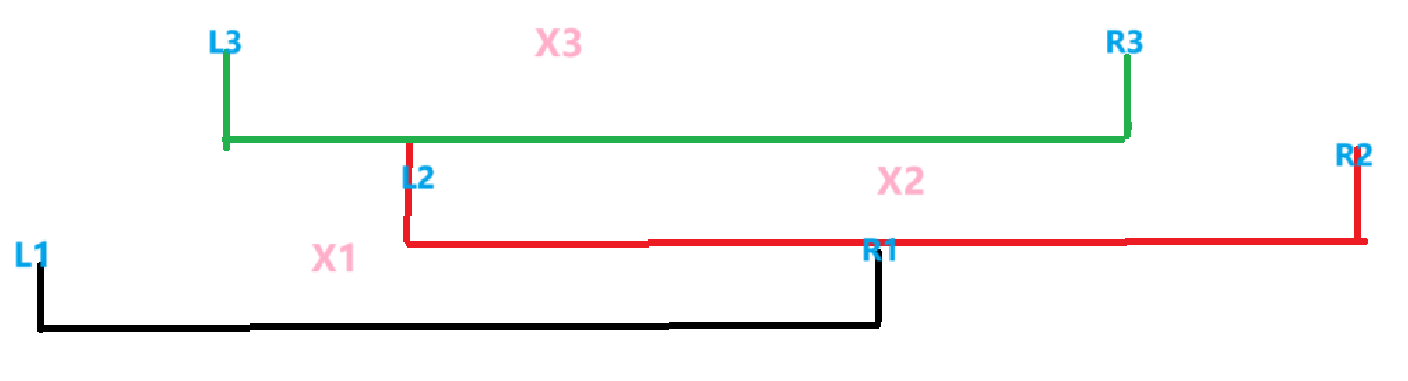
先不考虑种类问题,我们先考虑是队列存在多少个数问题。很容易发现某些地方重叠区域会加入多个数在当前点对应的队列当中。
我们容易知道最早的进队元素为 \(1\) 时刻的 \([l1,r1]\) 范围的队列增加 \(x_1\)。然后 \(2\) 时刻又在 \([l2,r2]\) 区间增加进 \(x_2\) 元素。比如考虑以下图:
可以发现比如 \([l2,r1]\) 中实际上的每个队列实际上是会增加两个元素的。假如说在 \([l2,r1]\) 区间上队列的最大容量为 \(1\),我们容易发现,在这个区间队列元素增加 \(2\) 以后,\(2 > 1\) 导致队首元素 \(x_1\) 被删掉,那么在 \(2\) 时刻这个区间上 \(x_1\) 就不再影响答案。那么抽象一下,对于每个点看做一个区间,容易发现对于每个时刻而言,总有一个时刻 \(t_{last} (\text{ 根据人为规定,也可能是 }m+1)\) 使得当前时刻 \(t_{curr}\) 插入的元素 \(x_{curr}\) 被弹出。
有一个良好的性质关于上述提到的 \(t_{last}\),容易发现每个时刻的 \(t_last\) 一定是单调递增的,因为根据队列的性质:先进先出,后进后出。很容易知道这样的 \(t_{last}\) 我们是可以通过单调性结合算法找到的。
暴力
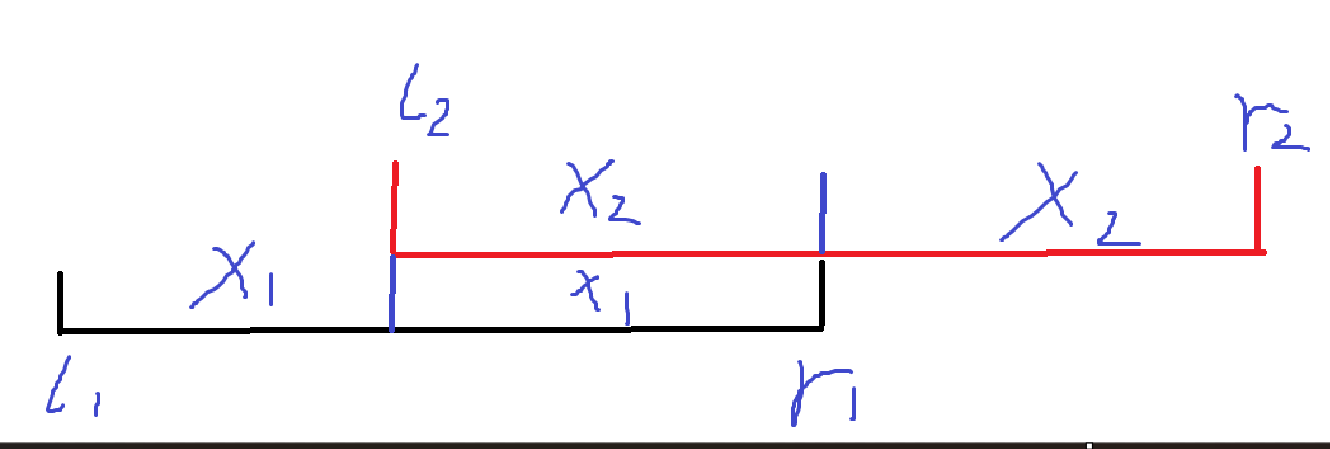
我们先来考虑下怎么暴力找单点 \(pos_{i}\) 的 \(t_{last}\),参照图 \(1\) 容易看出,我们固定查询点,假如为 \(l\),然后不断往后加入查询,假如加入的查询编号为 \(r\),容易发现,当加入某个查询时,会导致在 \(x\) 处的元素个数恰好 \(>\) \(a_{i}\) 队列容量。这个时候就会弹出队首元素 \(x\),反之如果有 \(a_i \ge cnt_{i}\),那么我们就可以不断移动 \(r\) 加入新查询知道。这个过程是具备单调性的,我们可以使用双指针轻松实现。而 \(l\) 移动到下一个查询,这个 \(r\) 由前面说的,是不会变小的,所以每个点对应的不同时间段的 \(t_{last}\) 可以使用双指针快速找到。但显然我们不能直接暴力去枚举单个点,这样复杂度直接爆了,但可以有个框架。
\(T_{last}\) 有啥用
找到每个点对应的时间段的 \(t_{last}\) 对于我们统计答案最终有啥用处。我们假如计算在 \(t_1\) 时刻的不同种类元素,很容易知道,由 \([l,r]\) 这个区间上每个点的 \(t_{last}\) 取最大值得到的 \(T_{last}\) 即为对于当前这个时刻加入的 \(x\) 的“生命周期”。存在的时间段即为 \([t_{curr},T_{last}]\),这样一来我们就知道了每个时间段的每个 \(x\) 的存活周期。我们可以画出图来。
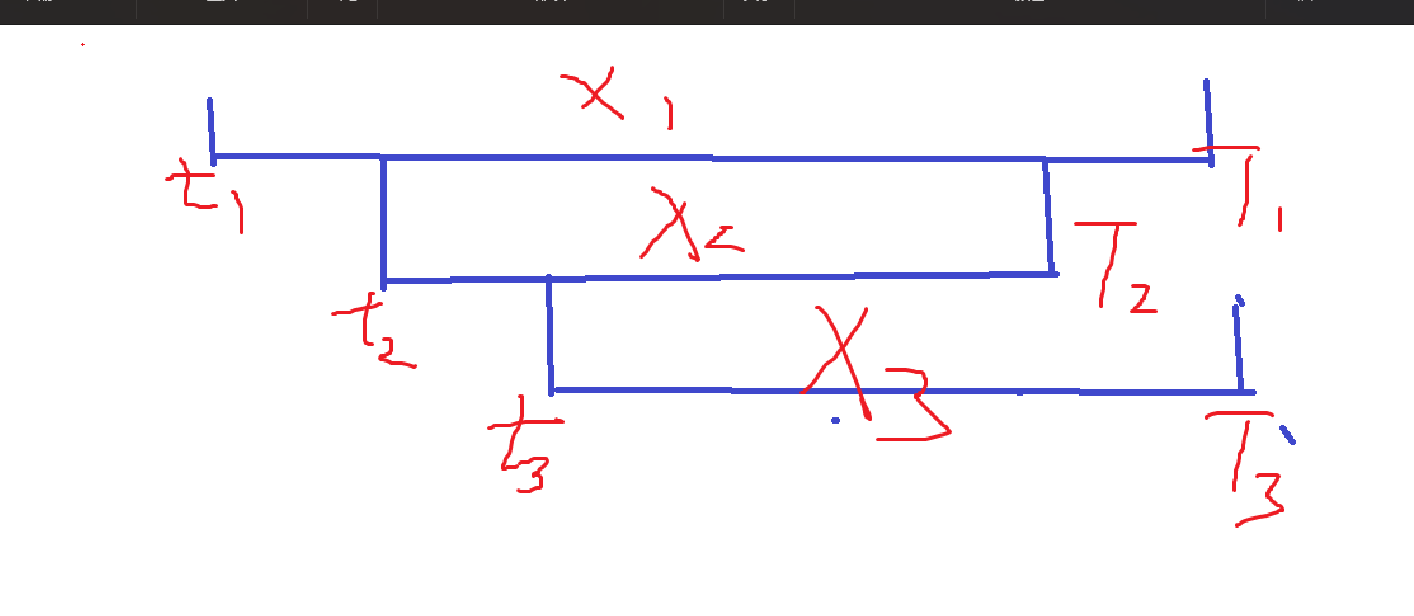
容易看出以时间轴为基准,每个 \(x\) 都有一个存活周期。问题转变为以下描述:
这个问题简单吧。\((\) emmmmmm,别说啥线段树分治一些复杂的做法,不带修直接离线扫描线开个桶就好了。
暴力到正解
比较容易观察到的一点是,如果一整个区间都被询问覆盖了,我们可以集体对这个区间进行操作。具体而言,知道这个区间的最大队列容量,我们的 \(x\) 要彻底消失,取决于最长的那个队列超出容量弹出 \(x\),所以我们对于一整个区间可以考虑维护区间加法和区间最值去进行操作判断双指针算法的 check。那么而显然的是,那么我们需要把原序列划分为一些区间进行操作,然后某些点我们可以上述说的暴力操作。显而易见的,考虑分块级别算法。
我们考虑下离线下查询,因为我们需要计算一个区间被完整的查询覆盖的次数,也即增加进的元素个数。所以我们可以逐块考虑所有查询对某个块的情况,我们容易画出以下图:

容易看出一共有三种情况:
- \(q_{1}\) 部分包含块区域,我们称之为散块查询。
- \(q_{2}\) 完全包含区域,我们称之为整块查询。
- \(q_{3}\) 无交集,我们直接忽略并跳过这个查询。
很显而易见的是,我们可以分整块对 \(t_{last}\) 的影响和散块对 \(t_{last}\) 的影响即可。整块很简单,我们考虑维护区间加标记,以及区间 \(max_{容量}\) 标记进行双指针判断。这里需不需要上什么线段树之类的区间修改打标记?其实不用的,这里需要重点提提。
整块影响
我们如果把所有的查询忽略 \(q_{3}\),可以写成“散----一堆整----散”这样的类型,当然中间整块查询数量可以为 \(0\)。大致可以写成这样 \(q_{2}q_{1}q_{1}q_{1}q_{1}q_{1}q_{2}\)。我们容易观察到,中间的整块查询的数量是可以直接就是 \(add_{区间}\) 的数量。在处理散块查询时,我们可以利用前缀和的方式,统计出两个散块之间的整块数量即可直接拿到一堆查询的 \(add\) 不需要枚举遍历。
这里要注意的是整块查询和散块查询都需要参与整块影响和散块影响当中,并不是独立的。整块影响下:
-
如果该加入的查询是整块查询,那么直接区间加标记 \(+1\)。
-
如果是散块查询,我们可以考虑暴力更新散块查询的区间 \([l,r]-1\),表示队列容量少了 \(1\) ,然后重算块最大容量。这个复杂度为 \(\sqrt{n}\),我们枚举块中每个点,在查询区间的才修改,然后同时重算块最大容量。
删除即为逆过程,完全同理。考虑复杂度,由于块长为 \(\sqrt{n}\),双指针算法和每次修改复杂度容易得知这个复杂度为 \(O(\sqrt{n} \times \sqrt{n})=O(n)\)。
散块影响
散块影响,我们只需要枚举块内每个点跑双指针就行。为了减少常数,快速查询某个区间上的整块数量,我们可以预处理出前缀和数组,并且我们预先重新整理查询,忽略掉 \(q_{3}\) 操作。在这里可以把整块查询用前缀和数组直接处理出来,所以只需要考虑散块查询对散块影响的情况。很简单的暴力,只需要在散块查询中跑双指针,和上述整块查询一致。当我们跑到了某个时间段 \([l,r]\) 需要分讨,\(l\) 为当前时间段。
考虑到 \(l\) 和 \(r\) 都为散块查询中的下标,并为包含整块查询,所以当枚举到 \(r\) 我们有以下两种情况:
-
如果此时此刻 \(r\) 依旧使得当前点对应的队列没有装满,考虑计算还差多少没装满,我们需要装满后然后再 \(+1\) 弹出队首元素,很轻易地可以计算出 \(need=max_{容量}- cnt_i+1\),而我们显然需要在当前 \(r\) 后继续往后走,后面只有两种情况,要么没查询 了,要么全是整块查询。我们只需要判断 \(r+need\) 和 \(m+1\) 取个最小值即可。现在这个位置的整块查询或者无查询才是最终的 \(last\)。
-
如果此时此刻有 \(r\) 恰好不满足,我们回溯一位后就和情况 \(1\) 一致了,然后算完再回溯回去。
容易知道枚举每个点的复杂度为 \(O(\sqrt{n})\),双指针在这里面不需要重新计算区间最大容量,因为是单点的,只需要关注单点队列最大容量就行,修改是 \(O(1)\),则单次双指针为 \(O(\sqrt{n})\)。所以散块影响的最终复杂度为 \(O(\sqrt{n}\times \sqrt{n}=O(n))\)
预处理完结束,来个 \(O(n)\) 跑离线扫描线即可。
更多详情可以参照代码注释:
参照带注释代码
#include <bits/stdc++.h>
//#pragma GCC optimize("Ofast,unroll-loops")
#define isPbdsFile
#ifdef isPbdsFile
#include <bits/extc++.h>
#else
#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>
#endif
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
template <typename T>
int disc(T* a, int n)
{
return unique(a + 1, a + n + 1) - (a + 1);
}
template <typename T>
T lowBit(T x)
{
return x & -x;
}
template <typename T>
T Rand(T l, T r)
{
static mt19937 Rand(time(nullptr));
uniform_int_distribution<T> dis(l, r);
return dis(Rand);
}
template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
return (a % b + b) % b;
}
template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
a %= c;
T1 ans = 1;
for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
return modt(ans, c);
}
template <typename T>
void read(T& x)
{
x = 0;
T sign = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')sign = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
x *= sign;
}
template <typename T, typename... U>
void read(T& x, U&... y)
{
read(x);
read(y...);
}
template <typename T>
void write(T x)
{
if (typeid(x) == typeid(char))return;
if (x < 0)x = -x, putchar('-');
if (x > 9)write(x / 10);
putchar(x % 10 ^ 48);
}
template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
write(x), putchar(c);
write(c, y...);
}
template <typename T11, typename T22, typename T33>
struct T3
{
T11 one;
T22 tow;
T33 three;
bool operator<(const T3 other) const
{
if (one == other.one)
{
if (tow == other.tow)return three < other.three;
return tow < other.tow;
}
return one < other.one;
}
T3() { one = tow = three = 0; }
T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
{
}
};
template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
if (x < y)x = y;
}
template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
if (x > y)x = y;
}
constexpr int N = 1e5 + 10;
int n, m;
int pos[N], s[N], e[N];
int blockSize, blockCnt; //块长,块数量
int a[N];
T3<int, int, int> qu[N];
int last[N];
int pre[N]; //整块用前缀和算贡献
int all[N]; //离线有关的查询,去掉无关查询
int sca[N]; //散块更新的查询编号
int tmp[N]; //临时计算整块贡献
//由第id个块更新每个修改的时间last
inline void update(const int id)
{
const int L = s[id], R = e[id];
//先考虑查询包括的整块能更新的时间末尾点,整块影响
int mx = 0;
forn(i, L, R)uMax(mx, tmp[i] = a[i]); //最大容量
int r = 0;
int add = 0; //整个块的addSize
//考虑加入/删除第curr个操作的影响
auto updateOpt = [&](const int curr, const int val)
{
auto [l,r,_] = qu[curr];
if (l > R or r < L)return; //不在里面不考虑
if (l <= L and R <= r)
{
add += val; //整块打增加标记
return;
}
//散块暴力修改,重算最大容量
mx = 0;
forn(i, L, R)
{
if (l <= i and i <= r)tmp[i] -= val;
uMax(mx, tmp[i]);
}
};
forn(l, 1, m)
{
auto [queryL,queryR,_] = qu[l];
while (r <= m and mx >= add)updateOpt(++r, 1); //不断加入新操作直到l所指操作对应的x被弹出
if (queryL <= L and R <= queryR)uMax(last[l], r); //如果查询包括整块,就可以用整块的l最后存在时间更新last了
updateOpt(l, -1);
}
//考虑查询包括的散块的last周期
//散块------一堆整块------散块-----一堆整块.... 抽象模型
forn(i, 1, m)pre[i] = 0; //用于作为前缀和做差优化找到一堆整块整体更新的addSize
int siz = 0, pointIdx = 0;
forn(i, 1, m)
{
const auto [l,r,_] = qu[i];
if (l > R or r < L)continue; //没有交集跳过这个查询
all[++siz] = i;
if (l <= L and R <= r)
{
//整块查询,addSize+1
pre[siz] = pre[siz - 1] + 1; //前缀的addSize +1
}
else
{
//散块add标记没变化,但需要记录需要处理的散块查询
pre[siz] = pre[siz - 1];
sca[++pointIdx] = siz;
}
}
//最后有可能这个操作一直都在,可以视为第m+1次从操作时才弹出
all[siz + 1] = m + 1;
int maxAdd;
//散块单点修改
auto Update = [&](const int i, const int queryId, const bool isFirst, const int val)
{
auto [l,r,_] = qu[all[sca[queryId]]];
if (!isFirst)maxAdd += (pre[sca[queryId]] - pre[sca[queryId - 1]]) * val; //散块之前的整块一并计入懒标记
if (l <= i and i <= r)maxAdd += val;
};
//删除左端点queryId,会失去下一个散块和当前散块之间的贡献
auto Del = [&](const int i, const int queryId)
{
auto [l,r,_] = qu[all[sca[queryId]]];
maxAdd -= pre[sca[queryId + 1]] - pre[sca[queryId]];
if (l <= i and i <= r)maxAdd--;
};
//暴力考虑单点last
forn(i, L, R)
{
maxAdd = 0;
mx = a[i];
//处理所有散块查询
r = 0;
forn(l, 1, pointIdx)
{
while (r < pointIdx and mx >= maxAdd)++r, Update(i, r, l == r, 1); //加入这个散块直到不能再加入
if (auto [queryl,queryr,_] = qu[all[sca[l]]]; queryl <= i and i <= queryr)
{
//对这组查询有影响
int idx = all[sca[l]];
if (mx < maxAdd)
{
Update(i, r, l == r, -1), r--; //最后一次操作导致恰好不满足,回退就满足了
int need = mx - maxAdd + 1; //还需要多少次(从右端点查询开始算)加入才能弹出所有点,刚好填满以后再加一个点就能弹出队首l对应的x
uMax(last[idx], all[min(sca[r] + need, siz + 1)]); //更新是哪个操作是最后一次单点弹出操作
r++, Update(i, r, l == r, 1); //移动到第一个恰好不满足点,至多移动一位
}
else
{
//mx>=maxAdd
//显然如果还剩余整块操作,last要么就是在整块操作里面,要么就是结束
int need = mx - maxAdd + 1; //还需要多少次(从右端点查询开始算)加入才能弹出所有点,刚好填满以后再加一个点就能弹出队首l对应的x
uMax(last[idx], all[min(sca[r] + need, siz + 1)]); //更新是哪个操作是最后一次单点弹出操作
}
}
Del(i, l);
}
}
}
int Cnt[N]; //桶计算元素个数
vector<int> child[N]; //离线扫描线
inline void solve()
{
// MyFile
cin >> n >> m;
blockSize = sqrt(n);
blockCnt = (n + blockSize - 1) / blockSize;
forn(i, 1, n)cin >> a[i], pos[i] = (i - 1) / blockSize + 1;
forn(i, 1, blockCnt)s[i] = (i - 1) * blockSize + 1, e[i] = i * blockSize;
e[blockCnt] = n;
forn(i, 1, m)cin >> qu[i].one >> qu[i].tow >> qu[i].three;
forn(i, 1, blockCnt)update(i);
forn(i, 1, m)child[last[i]].push_back(i); //离线扫描线构建
int res = 0;
forn(i, 1, m)
{
res += ++Cnt[qu[i].three] == 1;
for (int j : child[i])res -= --Cnt[qu[j].three] == 0;
cout << res << endl;
}
}
signed int main()
{
Spider
//------------------------------------------------------
int test = 1;
// read(test);
// cin >> test;
forn(i, 1, test)solve();
// while (cin >> n, n)solve();
// while (cin >> test)solve();
}