2022年的一本书，只有376页。证明直接去书里面找。

1 介绍
2 系数抽取和生成函数
3 RiordanGroup
4 特殊序列的RiordanArray的特征化
5 组合和以及反演
6 广义RiordanArray
7 RiordanGroup的存在性
8 RiordanArray的q-analog
9 正交多项式
习题解答
名词索引

1 介绍

1.1 啥是RiordanArray

1.2 源起和研究动机

1.3 基础的应用

\[\mathfrak{B}_r=\sum_{n \geq 0} \frac{1}{(r-1) n+1}\left(\begin{array}{c} r n \\ n \end{array}\right) z^n, \]

这个广义二项级数描述的是r-ary 数的生成函数。如果$r=2$，对应的是Catalan数；如果$r=3$，对应的是Ternary数$T_n=\frac{1}{2n+1} \tbinom{3n}{n}$

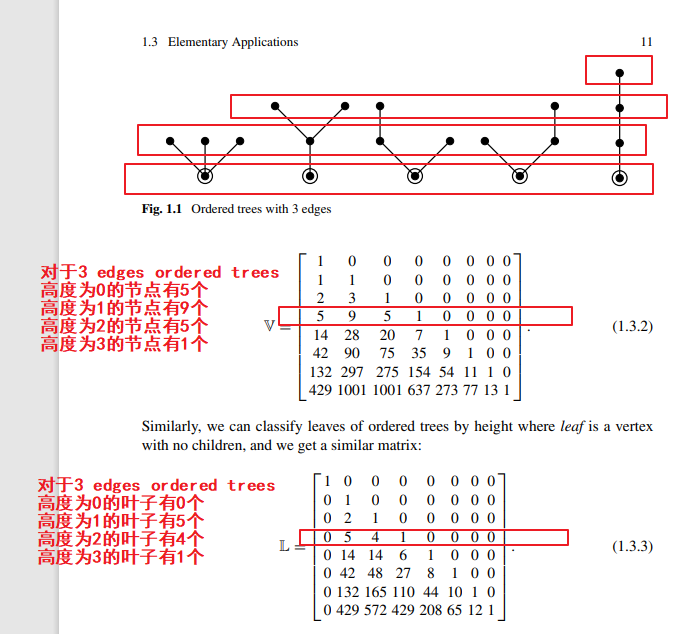
接着介绍 A-sequence of a family of trees
形式是序列$(a_0,a_1,a_2,\cdots)$，其中$a_k$是 updegree $k$的权重或数量。
因此，A-sequence给出了 the numebr of possibilities for the updegree of a vertex.

举例，一般我们设置$a_k=0$表示没有顶点具有updegree $k$。
$a_k=1$表示具有updegree $k$的顶点是允许的。

A-sequence的生成函数被称为updegree function，记为$A(z)$

举例， Motzkin树是ordered tree，满足每个顶点的updegree是$0,1,2$之一。所以对应的A-sequence是$(1,1,1,0,0,\cdots)$，A-function是$1+z+z^2$

Complex binary树对应的A-sequence是$(1,0,1,0,0,\cdots)$，A-function是$1+z^2$

incomplete binary树可以有right edge或者left edge，对应的A-function是$1+2z+z^2$

1.3节按照美式教材的套路告诉了你他是怎么发明这些概念的，怎么找到这些Theorems，formulae的。
但是如果你和我一样是工科生，你不关心这些，你首先关心的是解决问题的算法描述，如果有关于此算法的直观图像当然更好。

我理解的quick start是这样的：

你先了解UUR tree，RiordanArray，A-sequence，A-function这些概念。

知道我们在counting UUR trees时关心这3个矩阵。

\[\mathbb{V}:=(T,L_1)=\mathbb{T}\mathbb{L} \text{ and } \mathbb{L}:=(1,L_1) \text{ and } \mathbb{T}:=(T,z) \]

知道这些生成函数$T,L_1,L=1+L_1+L_1^2+L_1^3+\cdots$

你想定义一种新的UUR tree的时候，那你肯定要写出它对应的A-function。
你想计数：在边数为$n$的你这种UUR tree中，高度为$k$的树节点数目，那你关注$\mathbb{V}$矩阵。
你想计数：在边数为$n$的你这种UUR tree中，高度为$k$的叶子节点数目，那你关注$\mathbb{L}$矩阵。

你的问题是怎么从A-function得到这2个矩阵？

你打算先求出生成函数$T$，尝试从这个公式中计算出$T$：$ A(z T) =T$

接着用这个 $L_1=z \cdot A^{\prime}(z T).$ 算出$L_1$

之后就可以算出这3个矩阵了

常见的如下：

\[\begin{array}{c|c|c} \text { Type of UUR tree } & A \text {-sequence or } A \text{-function } & \mathbb{V}:=(T,L_1)=\mathbb{T}\mathbb{L} \text{ and } \mathbb{L}:=(1,L_1) \text{ and } \mathbb{T}:=(T,z) \text{ matrices } \\ \hline \text { ordered tree } & (1,1,1,1,1,1, \ldots) & T=C, L_1=zC^2 \text{ where C is g.f. of Catalan numbers} \\ \text { Motzkin tree } & (1,1,1,0,0,0, \ldots) \\ \text { incomplete binary tree } & (1,2,1,0,0,0, \ldots) \\ \text { complete binary tree } & (1,0,1,0,0,0, \ldots) \\ \text { even tree } & (1,0,1,0,1,0, \ldots) \\ \text { incomplete ternary tree } & (1,3,3,1,0,0, \ldots) \\ \text { complete ternary tree } & (1,0,0,1,0,0, \ldots) \\ \text { Schröder tree } & (1,2,2,2,2,2, \ldots) \\ \text { spoiled child tree } & (1,2,1,1,1,1, \ldots) \\ \text { Hex tree } & (1,3,1,0,0,0, \ldots) \\ \text { Gamma tree } & (1,0,1,1,1,1, \ldots) \\ \text { simple tree (path) } & (1,1,0,0,0,0, \ldots) \\ \text { Traffic light tree} & A(z)=1/(1-z)^2 & T=g^2, L_1=2(g-1) \text{ where g is g.f. of tenary numbers} \end{array} \]

(*用于快速验证的Mathematica代码*)

Clear["Global`*"]

RiordanArray[p_, q_, numOfRows_Integer] := 
  Table[SeriesCoefficient[p*q^k, {z, 0, n}], {n, 0, numOfRows}, {k, 0,
      n}] // Grid;
GenerateMatricesVLT[T_, L1_, numOfRows_Integer] := 
 Module[{MatrixV, MatrixL, matrixT}, 
  MatrixV = RiordanArray[T, L1, numOfRows]; 
  MatrixL = RiordanArray[1, L1, numOfRows]; 
  MatrixT = RiordanArray[T, z, numOfRows];
  {MatrixV, MatrixL, MatrixT}]


CatalanGF = Sum[CatalanNumber[n]*z^n, {n, 0, Infinity}];
GenerateMatricesVLT[CatalanGF, z*CatalanGF^2, 8]


TenaryNumberGF = Sum[Binomial[3 n, n]/(2*n + 1)*z^n, {n, 0, Infinity}];
GenerateMatricesVLT[TenaryNumberGF^2, 2 (TenaryNumberGF - 1), 8]

$\textbf{Theorem 1.1}$ 介绍Couting UUR trees的五个基本方程：

\[(a) V=T L; \\ (b) V=(z T)^{\prime}; \\ (c) L=\frac{1}{1-L_1} = 1+L_1 +L_1^2 + L_1^3 +L_1^4 + \cdots; \\ (d) L_1=z T^{\prime} / V; \\ (e) L_1=z A^{\prime}(z T). \]

练习

点击展开

1.1 使用等式(1.3.1)找到如下RiordanArray矩阵的$(n,k)$元素的闭形式：
(1) 例子1.1中的$\mathbb{V}=(C,zC^2)$， $\mathbb{L}=(1,zC^2)$，其中$C$是Catalan数的生成函数
(2) 例子1.2中的$\mathbb{V}=(g^2,2(g-1))$，$\mathbb{L}=(1,2(g-1))$，其中$g$是ternary数的生成函数。

1.2 证明$L_1=zA'(zT)$. 见定理1.1的(e)
1.3 解出交通信号灯树的方程，其中，对于任意一个有正updegree的顶点至少有一个绿边。

1.4 说明，对于交通信号灯树

\[\frac{\left[z^n\right] L_1}{\left[z^n\right] T}=\frac{\left[z^n\right] 2(g-1)}{\left[z^n\right] g^2}=\frac{2 \cdot \frac{1}{3 n+1}\left(\begin{array}{c} 3 n+1 \\ n \end{array}\right)}{\frac{2}{3 n+2}\left(\begin{array}{c} 3 n+2 \\ 2 \end{array}\right)}=\frac{2 n+2}{3 n+1} \rightarrow \frac{2}{3} \]

参考

2 系数抽取和生成函数

2.1 形式幂级数

2.2 系数抽取

2.3 拉格朗日反演定理

2.4 生成函数

练习

点击展开

2.1 证明如果$f(t)=\mathcal{G}(f_k)$是序列$(f_k)_{k\in \mathbb{N}}$的生成函数，那么

\[\mathcal{G}\left(f_{k+2}\right)=\frac{\mathcal{G}\left(f_k\right)-f_0-f_1 t}{t^2} \]

以及，更一般地，

\[\mathcal{G}\left(f_{k+j}\right)=\frac{\mathcal{G}\left(f_k\right)-f_0-f_1 t-\cdots-f_{j-1} t^{j-1}}{t^j} . \]

2.2 证明，如果$f(t)=\mathcal{G}(f_k)$是序列$(f_k)_{k\in \mathbb{N}}$的生成函数，那么

\[\mathcal{G}\left((k+1) f_{k+1}\right)=D \mathcal{G}\left(f_k\right) \]

2.3 证明，如果$f(t)=\mathcal{G}(f_k)$是序列$(f_k)_{k\in \mathbb{N}}$的生成函数，那么

\[\mathcal{G}\left(k^2 f_k\right)=t D \mathcal{G}\left(f_k\right)+t^2 D^2 \mathcal{G}\left(f_k\right) \]

2.4 证明，如果$f(t)=\mathcal{G}(f_k)$是序列$(f_k)_{k\in \mathbb{N}}$的生成函数，那么

\[\mathcal{G}\left(k^{\underline{r}} f_k\right)=t^r D^r \mathcal{G}\left(f_k\right), \]

其中 $ k^{\underline{r} = k (k-1) \cdots (k-r+1)$是下降乘

2.5 证明，如果$f(t)=\mathcal{G}(f_k)$是序列$(f_k)_{k\in \mathbb{N}}$的生成函数，那么

\[\mathcal{G}\left(p^k f_k\right)=f(p t) . \]

2.6 证明，如果$H_n=\sum\limits_{i=1}^{n} \frac{1}{i}$是第$n$个harmonic number

\[\begin{gathered} \mathcal{G}\left(n H_n\right)=\frac{t}{(1-t)^2}\left(\ln \frac{1}{1-t}+1\right) \\ \mathcal{G}\left(\frac{1}{n+1} H_n\right)=\frac{1}{2 t}\left(\ln \frac{1}{1-t}\right)^2 . \end{gathered} \]

2.7 证明下面的等式:

\[\begin{aligned} \mathcal{G}\left(k\left(\begin{array}{l} p \\ k \end{array}\right)\right) & =p t(1+t)^{p-1} \\ \mathcal{G}\left(k^2\left(\begin{array}{l} p \\ k \end{array}\right)\right) & =p t(1+p t)(1+t)^{p-2} \\ \mathcal{G}\left(\frac{1}{k+1}\left(\begin{array}{l} p \\ k \end{array}\right)\right) & =\frac{(1+t)^{p+1}-1}{(p+1) t} \\ \mathcal{G}\left(k\left(\begin{array}{l} k \\ m \end{array}\right)\right) & =\frac{m t^m+t^{m+1}}{(1-t)^{m+2}} \\ \mathcal{G}\left(k^2\left(\begin{array}{l} k \\ m \end{array}\right)\right) & =\frac{m^2 t^m+(3 m+1) t^{m+1}+t^{m+2}}{(1-t)^{m+3}} \\ \mathcal{G}\left(\frac{1}{k}\left(\begin{array}{l} k \\ m \end{array}\right)\right) & =\frac{t^m}{m(1-t)^m} \text { form }>0 . \end{aligned} \]

2.8 证明

\[\sum_{k=0}^n \frac{k}{(k+1) !}=1-\frac{1}{(n+1) !} \]

2.9 blablabla

参考

3 RiordanGroup

3.1 RiordanArray和RiordanGroup

3.2 一些特殊的子群

3.3 RiordanGroup的一些看法

练习

点击展开

3.1 证明Lagrange子群和Bell子群同构
3.2 证明Riordan群的元素$M=(1,-t)$的中心化子centralizer是 checkerboard子群。
3.3 证明checkerboard子群是multi-checkerboard subgroup的子群
3.4 证明所有具备形式$(C(t) / C(f(t)), f(t))$的Riordan矩阵的 set？集合是 Riordan群的一个 (stablizer) subgroup

参考

4 特殊序列的RiordanArray的特征化

4.1 A-序列和Z-序列

4.2 A-矩阵

4.3 它是一个RiordanArray吗？

练习

点击展开

4.1 找到RiordanArray $\mathcal{R}\left(\frac{1}{1-t}, \frac{t(1+r t)}{1-t}\right) \text { for } r \in \mathbb{R} \text {. }$的 A-序列和Z-序列

4.2

参考

5 组合和以及反演

5.1 组合和

5.2 组合反演

练习

点击展开

5.1 计算下面的组合和

\[\sum\limits_{k=1}^{n} \tbinom{n}{k} \frac{(-1)^{k-1}}{k} \]

5.2 证明下面的组合等式

\[\sum_{k=0}^n\left(\begin{array}{l} n \\ k \end{array}\right)(k+1)=(n+2) 2^{n-1} \]

5.3 证明下面的组合等式

\[\sum_{k=0}^n(-1)^{n-k}\left(\begin{array}{l} n+k \\ n-k \end{array}\right) 4^k=2 n+1 . \]

参考

6 广义RiordanArray

6.1 三维RiordanGroup

6.2 三维RiordanArray

6.3 RiordanArrays和ShefferSequences的联系

6.4 特殊的RiordanArrays和ShefferSequences

6.5 双RiordanArrays和ShefferPolynomial对

练习

点击展开

6.1

...

6.8 使用指数RiordanArrays证明$b$阶Gould等式：

\[\sum_{k=b}^n \frac{\gamma-\beta b}{\gamma-\beta k}\left(\begin{array}{c} \gamma-\beta k \\ k-b \end{array}\right)\left(\begin{array}{c} \alpha+k \beta \\ n-k \end{array}\right)=\left(\begin{array}{c} \alpha+\gamma \\ n-b \end{array}\right) \]

参考

7 RiordanGroup的存在性

7.1 三维RiordanGroup

7.2 三维RiordanArray

7.3 多变量的RiordanGroup

8 RiordanArray的q-analog

8.1 组合q-analogs

8.2 欧拉生成函数

8.3 q-Riordan Arrays

8.4 q-Riordan Arrays的应用

练习

点击展开

8.1 说明$q-$factorial $[n]_q !$ counts permutations while keeping track of the number of inversions.

8.2 证明和、积、商的q-derivative公式。

8.3 证明q-Pascal等式，对于$0< |q| <1$:

\[\left(\begin{array}{c} \alpha+1 \\ k \end{array}\right)_q=\left(\begin{array}{l} \alpha \\ k \end{array}\right)_q q^k+\left(\begin{array}{c} \alpha \\ k-1 \end{array}\right)_q=\left(\begin{array}{l} \alpha \\ k \end{array}\right)_q+\left(\begin{array}{c} \alpha \\ k-1 \end{array}\right)_q q^{\alpha+1-k} \]

8.4 让$V_n$表示在$GF(q)$伽罗瓦域上的$n$维向量空间，$q=p^n$。证明$V_n$子空间的伽罗瓦数是：

\[G_n=\sum\limits_{k=0}^{n} \tbinom{n}{k}_q \]

8.5 证明下面这些：
(1) 环$\mathcal{R}_q$是一个群，当且仅当$q=0$或$q=1$。
(2) 子群$\left\{(g, z)_q: g \in \mathcal{E}_q(0)\right\}$形成一个群。

8.6 第二类斯特林数的q-analog被定义为：

\[\sum_{n \geq k}\left\{\begin{array}{l} n \\ k \end{array}\right\}_q \frac{z^n}{[n]_{q} !}=\frac{\left(e_q(z)-1\right)^{[k]}}{[k]_{q} !} . \]

利用公式(8.4.8)找到如下q-Riordan矩阵的前5行：

\[\left(1, e_q(z)-1\right)_q=\left(\left\{\begin{array}{l} n \\ k \end{array}\right\}_q\right)_{n, k \in \mathbb{N}} \]

8.7 blablabla

8.8 让$f(z)$是定理8.2里的欧拉生成函数。证明存在唯一的

right q-comppositional inverses of $f$ if and only if $f_1 \neq 0$

参考

9 正交多项式

9.1 正交多项式和Riordan Arrays

9.2 指数RiordanArray和经典正交多项式

9.3 正交多项式作为矩

9.4 组合多项式作为RiordanArray的矩

9.5 连分数和RiordanArray

练习

点击展开

9.1 说明和RiordanArray $(\frac{1}{1+x^2}, \frac{x}{1+x^2})$的矩对应的数列是 the aerated Catalan numbers
9.2 说明和RiordanArray $ ( \frac{1}{1+x} , \frac{x}{(1+x)^2}) $的矩对应的数列是 the Catalan numbers $C_n$
9.3 说明和RiordanArray $\left(\frac{1}{(1+x)^2}, \frac{x}{(1+x)^2}\right)$ 的矩对应的是 the shifted Catalan numbers $C_{n+1}$

9.4 说明和RiordanArray $\left(\frac{1}{1+x+x^2}, \frac{x}{1+x+x^2}\right)$ 的矩对应的是 Motzkin数 $M_n=\sum_{k=0}^{\left\lfloor\frac{n}{2}\right\rfloor}\left(\begin{array}{c} n \\ 2 k \end{array}\right) C_k$

9.5 说明和RiordanArray $\left(\frac{1+x}{1+x+x^2}, \frac{x}{1+x+x^2}\right)$ 的矩对应的是 Riordan numbers, A005043

9.6 说明和RiordanArray $\left(\frac{1}{1+x}, \frac{x}{1+3 x+2 x^2}\right)$的矩对应的是 the little Schröder numbers.

9.7 说明和RiordanArray $\left(\frac{1}{1+2 x}, \frac{x}{1+3 x+2 x^2}\right)$ 的矩对应的是 large
Schröder numbers $S_n=\sum_{k=0}^n\left(\begin{array}{c} n+k \\ 2 k \end{array}\right) C_k$

9.8 说明和RiordanArray $\left(\frac{1-x}{1+x}, \frac{x}{(1+x)^2}\right)$ 的矩对应的是 the central binomial numbers $\tbinom{2n}{n}$

9.9 说明和RiordanArray $\left(\frac{1-x}{1+x^2}, \frac{x}{1+x^2}\right)$ 的矩对应的是 the central binomial numbers $\left(\begin{array}{c} n \\ \left\lfloor\frac{n}{2}\right\rfloor \end{array}\right)$

9.10 说明和RiordanArray $\left(\frac{1-x}{(1+x)^2}, \frac{x}{(1+x)^2}\right)$的矩对应的数是 $\tbinom{2n+1}{n+1}$