1 AIG概述
在前面的博文《Quine-McCluskey两级逻辑化简算法》中,我们介绍了两级逻辑的局限性。事实上主流EDA采用多级逻辑表示大规模布尔函数。本文介绍的AIG就属于多级逻辑表示法的一种。
AIG(AND-INV Graph)是由与门和非门构成的布尔网络,可有效地描述和操作大规模布尔函数。
AIG是一个DAG,每个结点表示一个二输入与门,而弧表示连接。弧上标圈为反相弧(通过非门),无圈为同相弧(恒等)。
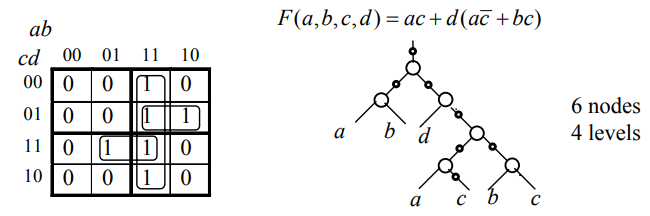
(图1.1 注:省略弧的箭头时默认从下往上)
区别于树,AIG可以共享布尔表达式中的公共子表达式(允许多扇出)
区别于一般的有向图,AIG不能含有组合逻辑环。
另外,结构上的限制使AIG具有一些优良性质:
- (1)AND结点的入弧可交换
- (2)对于从结点p生成的子图\(G'(V(p),E(p))\),其中
\(L_p,R_p\)分别是p结点的左右孩子(若存在),\(E(p)\)是弧头与弧尾都属于V(p)的所有边。
满足:
1)若从某一输入结点扇出的同相弧和反相弧都与G'(p)邻接,则p输出恒为0,因为\(x \wedge \neg x\)永假。
2)任意改变G'(p)的边,若G'仍为弱连通的AIG,且p为拓扑序列的最后一个结点,则G'(p)与G(p)逻辑等价。因为布尔与运算满足交换律和结合律。
实际上子图\(G'(V(p),E(p))\)是一个supergate,即多输入AND。
- (3)还有很多……
这些性质便于后续算法设计。
2 AIG约简
AIG不是标准型,即相同布尔函数可对应不同的AIG。这导致AIG可存在结构不同,但功能重复的子图,需要约简。
例如,下图AIG与上文图1.1表示的是同一布尔函数:
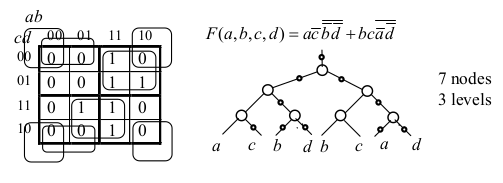
通过最小项容易验证这两AIG逻辑等价,因为最小项之和是标准型。
2.1 Structural Hash
Structural Hash(简写为strash)复用结构相同的子图。
考虑到时间复杂度,一般最多实现2级strash。
一级strash
一级strash复用结构相同的层次为1的子图(这种子图最多2输入)。
在构造AIG每添加一个结点前,先检查图中是否已有扇入边相同的结点,若有,直接复用现成结点输出。
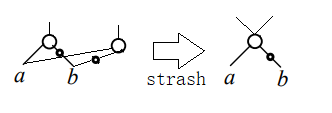
具体实现:可维护一张散列表,以AIG中结点的两条扇入边的Hash(.)为键,而结点指针为值。
添加结点前,以扇入为键查表,确认新结点是否冗余。若非冗余,再加入AIG和散列表中。
两级strash
注意层次为2的AIG子图最多有4个输入,最多能表示\(2^{2^4}=65536\)个不同的布尔函数。
预处理:考虑到AIG两级子图能表示的布尔函数是有限的,且数量不多。对每个布尔函数,枚举所有可能的两级子图,选择一个作为标准型,插入散列表LKP。
每添加一个结点时,以该结点为根的二级子图(若存在)为键,从LKP查找对应标准型,然后直接构造其标准型,过程中利用一级strash实现结构复用。因为构造的都是标准型,结构相同成为了布尔函数等价的充分条件。
原始子图中有结点可能未被用到(输出悬空),最后还需进行垃圾回收。
下图中,结点2的逻辑锥函数为\(f(2)=\overline{(a\overline{b})}b=b\),假设选取f=b作为子图\(\overline{(a\overline{b})}b\)的标准型。
构造右图的AIG时,首先按拓扑序插入结点a、b、1,然后插入结点2,此时在LKP中可查找到子图\(\overline{(a\overline{b})}b\),得到标准型f=b,直接构造标准型,导致结点2悬空,后被垃圾回收。子图\(\overline{(b\overline{c})}\overline{b}\)同理,最终得到右图结果。
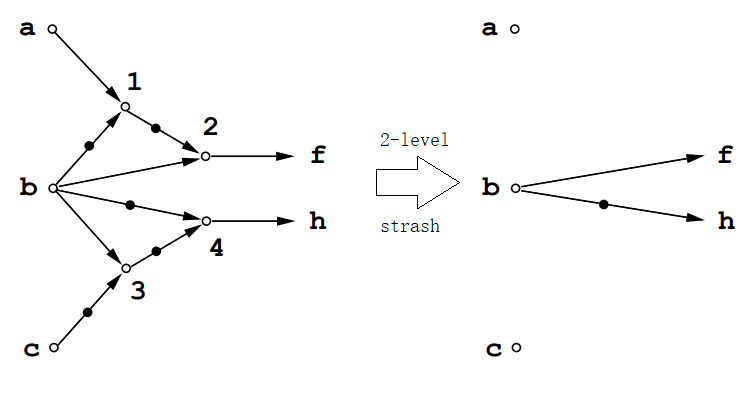
两级strash的详细实现可参考[1]。
2.2 Functional Reduce
一级strash的缺点很明显:因为AIG不是标准型,相同布尔函数可能对应不同的AIG结构,此时仅从结构上无法约简,必须验证逻辑等价性。
Functional Reduce(简写为FR)确保AIG中任意两个结点所对应的逻辑锥函数互不相同,即功能唯一。
逻辑锥(cone)
逻辑锥是广泛使用的一个概念。以输出结点p为根的逻辑锥定义为:
(假设Primary Input结点没有入弧)
例如下图结点e的逻辑锥为:
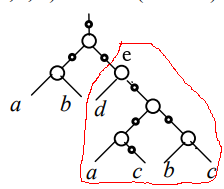
回到FR原理,原始论文[2]用到了验证功能等价性的两种方法:逻辑仿真和组合等价类检查(CEC)。
随机仿真
针对结点p的逻辑锥随机产生一组激励,计算p在对应激励下的响应。对于两个不同结点n1,n2,分别仿真相同激励V下的响应f1(V),f2(V)。若:
- \(f1(V)\ne f2(V)\),则p1,p2对应逻辑锥函数不同
- \(f1(V)= f2(V)\),若V不完备,则无法判断;否则相同
随机仿真的意义在于以一定概率排除不等价的结点,避免执行耗时的证明。对于大规模组合逻辑,仿真在有限时间内很难做到完备,因为k变量激励有\(2^k\)个。对于无法判断的结点,需要引入形式化证明方法。
SAT与等价类检查
证明两逻辑锥n1,n2功能是否相同,实际上就是证明\(p_1(V) \oplus p_2(V)=0\)对任意V成立。n1,n2异或称为miter。
miter的验证可转换为SAT问题,只需把miter转换为CNF,判断可满足性:
- 可满足,n1和n2功能不同,对应真值指派即为使两者输出相异的反例。
- 不可满足,n1和n2功能等价。
结合上述两种方案,可以判断两个逻辑锥是否等价,将等价的合并在一起(使用strash相同的合并方法)。
FR得到的是无逻辑冗余的AIG,可以方便地应用于形式验证、逻辑化简等。
参考文献
[1] M. K. Ganai, A. Kuehlmann, “On-the-fly compression of logical circuits”. Proc. IWLS '00.
[2] Mishchenko A , Jiang R , Chatterjee S , et al. FRAIGs: Functionally reduced AND-INV graphs. American Physical Society, 2004.