2023-07-11 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(六)
回顾上节的最速下降法的特征:最速下降法迭代路径呈锯齿状,即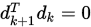 . 这一节给出共轭的概念,其是正交性的推广,然后给出共轭方向(梯度)法.
. 这一节给出共轭的概念,其是正交性的推广,然后给出共轭方向(梯度)法.
**定义 1.7 ** 设 是
是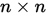 对称正定矩阵,
对称正定矩阵,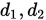 是
是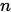 维非零向量. 如果
维非零向量. 如果
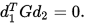
那么称向量
 和
和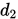 是
是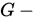 共轭的 (或共轭).
共轭的 (或共轭).
自然地, 两个向量的共轭可以推广到 个向量共轭. 设
个向量共轭. 设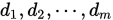 是
是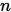 维非零向量组,如果
维非零向量组,如果
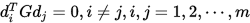
那么称
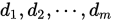 是
是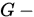 共轭的. 即两两
共轭的. 即两两 共轭.
共轭.
命题 1.2 设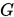 为
为 阶对称正定矩阵,若非零向量组
阶对称正定矩阵,若非零向量组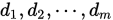 是
是 共轭的,则
共轭的,则 是线性无关的.
是线性无关的.
证明只需要假设存在一组常数 使得向量组线性相关,然后证得
使得向量组线性相关,然后证得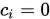 即可.
即可.
命题 1.3 设 为
为 阶对称正定矩阵,若非零向量组
阶对称正定矩阵,若非零向量组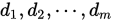 是
是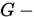 共轭的. 若
共轭的. 若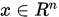 与
与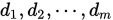 都直交,即
都直交,即 , 则
, 则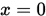 .
.
注意到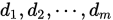 构成
构成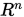 中的一组基(命题 1.2), 则
中的一组基(命题 1.2), 则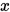 可由
可由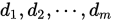 表示,由
表示,由 即得
即得 .
.
下面给出共轭方向法的算法:
Step 1. 取初始点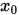 , 搜索方向
, 搜索方向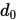 满足
满足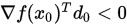 , 精度
, 精度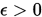 ,
, 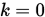
Step 2. 若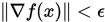 , 置
, 置 则停止, 否则转下步.
则停止, 否则转下步.
Step 3. 线搜索:
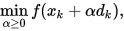

Step 4. 选取搜索方向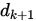 满足
满足
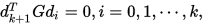
其中
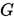 是对称正定矩阵.
是对称正定矩阵.
Step 5. 令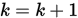 , 转 Step 2.
, 转 Step 2.
上述算法中,令人疑惑的地方在于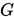 的选择和搜索方向的计算,其中搜索方向可以由一个线性方程组给出。
的选择和搜索方向的计算,其中搜索方向可以由一个线性方程组给出。
那么共轭方向法在什么情况下收敛到最优解呢,下面的定理将给出答案。
定理 1.8 设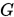 是
是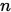 维对称正定矩阵,
维对称正定矩阵, 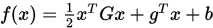 ,
,  是任意初始点. 若搜索方向
是任意初始点. 若搜索方向 是
是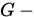 共轭的,
共轭的, 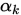 是精确线搜索步长,
是精确线搜索步长, 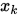 是共轭方向法产生的迭代点, 则有
是共轭方向法产生的迭代点, 则有
(1) 对每一个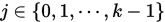
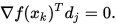
(2) 算法至多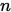 次迭代可得无约束优化问题的最优解.
次迭代可得无约束优化问题的最优解.
证明:
(1) 由 以及
以及 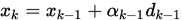 和
和
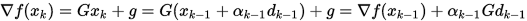
反复带入上式,得到
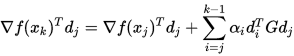
由于
 是
是 共轭的,所以
共轭的,所以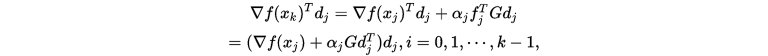
即
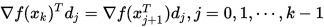
由于
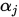 是精确线搜索的步长 (即
是精确线搜索的步长 (即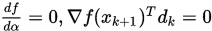 ),因此
),因此
(2) 由于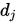
 共轭,再有
共轭,再有 可知
可知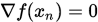 , 即
, 即 是
是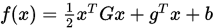 .
.
二次终止性 若算法对任意的正定二次函数,从任意初始点出发,都能经过有限步达到其最优点,则称算法具有二次终止性.
正定二次函数中的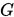 即可看作是一般可导函数的Hesse矩阵,只不过
即可看作是一般可导函数的Hesse矩阵,只不过 不被当前迭代点的位置影响.
不被当前迭代点的位置影响.
1. 共轭梯度法
如果在共轭方向发中利用目标函数的梯度来产生共轭方向,那么就称这样的方法维共轭梯度法.
下面给出生成正定二次函数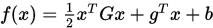 的共轭梯度方向的方法.
的共轭梯度方向的方法.
给定初始点 ,
,  . 如果对于第
. 如果对于第 次迭代,
次迭代, 是精确线搜索步长,要求
是精确线搜索步长,要求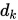 与
与 是
是 共轭的且是下降方向,假设
共轭的且是下降方向,假设

通过选择合适的
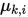 , 可以使得
, 可以使得 与之前的
与之前的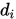
 共轭, 因此有
共轭, 因此有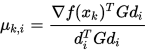
这就确定了下一步的下降方向.
上述公式中每一步的下降方向都与前面所有的下降方向有关,且需要计算当前点的Hesse矩阵,使得算法的复杂性较高. 下面给出一些更简单的下降方向的计算方法.
定理 1.9 设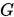 是
是 维对称正定矩阵,
维对称正定矩阵,  ,
, 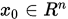 是任意初始点. 若搜索方向如
是任意初始点. 若搜索方向如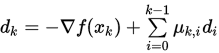 ,
, 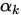 是精确搜索步长,
是精确搜索步长,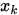 是由共轭梯度法产生的迭代点,则
是由共轭梯度法产生的迭代点,则
(1) 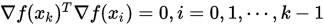 ;
;
(2)  ;
;
(3)  .
.
证明: (1) 由于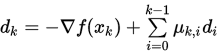 , 因此
, 因此

又由于共轭方向法都有对:每一个
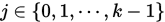
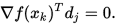
因此
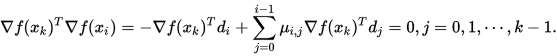
(2) 由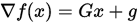 ,
, 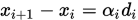 有
有
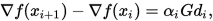
以及
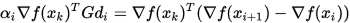
因此
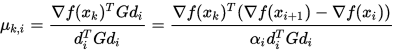
由 (1) 可知分式上半部分为0, 因此 (2) 成立.
(3)
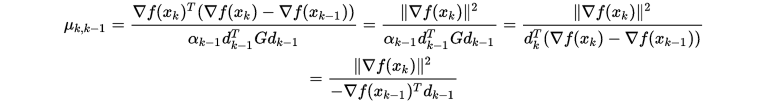
带入
 以及定理 1.8 的(1)即得
以及定理 1.8 的(1)即得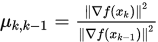 .
.
通过上面的证明能够得到几种不同的下降方向迭代格式:
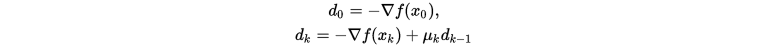
其中
 在不同取值下有
在不同取值下有
- Fletcher-Reeves公式(FR公式)
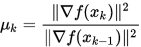
- Crowder-Wolf 公式
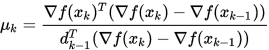
- Polak-Ribiere-Polyak 公式

- Dixon 公式
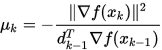
- Dai-Yuan 公式

上面五个公式虽然形式有所不同,但是都是在定理1.9证明中出现过的等价形式,即目标函数是正定二次函数且采用精确线搜索时,这些公式是等价的. 但是对于一般的优化问题,上述搜索方向并不等价.
由于共轭方向对多能生成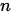 个,因此对于一般目标函数当迭代次数大于
个,因此对于一般目标函数当迭代次数大于 时需要重置下降方向,如下所示
时需要重置下降方向,如下所示
算法 7 FR共轭梯度法
Step 1. 选取初始点 , 给定精度
, 给定精度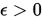 .
.
Step 2. 计算 , 置
, 置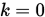 .
.
Step 3. 做线搜索
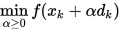
得到
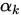 和
和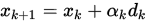 .
.
Step 4. 如果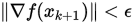 , 则停止算法,
, 则停止算法, 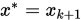 ; 否则转下步.
; 否则转下步.
Step 5. 如果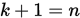 , 则令
, 则令 , 转Step 1.; 否则转下步.
, 转Step 1.; 否则转下步.
Step 6. 计算
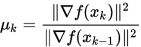
置
 , 转Step 2.
, 转Step 2.
定理 1.10 设无约束优化问题的目标函数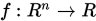 连续可微且有下界,梯度
连续可微且有下界,梯度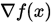 是Lipschitz连续. 若采用精确线搜索的FR共轭梯度法产生无穷点列
是Lipschitz连续. 若采用精确线搜索的FR共轭梯度法产生无穷点列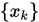 , 则
, 则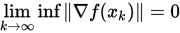 .
.
定理 1.10 说明FR共轭梯度法对于一般的连续可微有下界函数是可以收敛到局部最优解的,FR最开始提出可能是 Function minimization by conjugate gradients, Fletcher and Reeves.
 070149.pdf
3.21 MB
070149.pdf
3.21 MB
下面是FR共轭梯度法的Matlab实现
- % Fletcher-Reeves 共轭梯度法
- function [x xlog] = FRCG(f, x0, epsilon)
- % f 目标函数,函数句柄
- % g 梯度函数 函数句柄
- % epsilon 精度要求
- % method 线搜索方法
- k = 0;
- iter = 0;
- maxIt = 1e4;
- n = length(x0);
- d1 = - My_Gradient(f, x0);
- while iter <= maxIt
- [alpha tx] = SuccFa(f, 1, x0, d1, 1, epsilon, 1e4);
- x1 = x0 + alpha * d1;
- d2 = My_Gradient(f, x1);
- xlog(iter+1) = norm(d2);
- x = x1;
- x0 = x1;
- if norm(d2) < epsilon
- break
- end
- if k+1 == n
- d1 = - My_Gradient(f, x0);
- k = 0;
- else
- d1 = - d2 + d1 * norm(d2)^2/norm(d1)^2;
- k = k+1;
- end
- iter = iter + 1;
- end
- end
- function [alphak xlog] = SuccFa(fun, alpha, x0, diff_x, h, epsil, maxIt)
- k = 0;
- xlog = alpha;
- while k <= maxIt
- alphak = alpha + h;
- if fun(x0 + alphak * diff_x) < fun(x0 + alpha * diff_x)
- h = 2 * h;
- alpha = alphak;
- else
- h = - h / 4;
- end
- k = k + 1;
- xlog(k) = alphak;
- if abs(h) < epsil
- break
- end
- end
- end
- function [x] = F_alpha(alpha)
- x = f(x0 + alpha * diff_x);
- end
- function [gd] = My_Gradient(f, x)
- gd = x;
- epsil = 1e-5;
- d = [-2* epsil, -epsil 0 epsil 2*epsil];
- tx = [x x x x x];
- fx = [0,0,0,0,0];
- for i = 1:length(x)
- tx(i,:) = tx(i,:) + d;
- for h = 1:5
- fx(h) = f(tx(:,h));
- end
- gf = gradient(fx);
- gd(i) = gf(3);
- end
- end
测试程序
- f = @(x) sin(x(1)) + cos(x(2));
- x0 = [1, 1]';
- epsilon = 1e-6;
- [x xlog] = FRCG(f, x0, epsilon)
- %% 书上的例子
- f = @(x) 2*x(1)^4 - 4 * x(1)^2*x(2) + x(1)^2 + 2* x(2)^2-2*x(1)+5;
- x0 = [0 ,0]';
- epsilon = 1e-6;
- [x xlog] = FRCG(f, x0, epsilon)
结果表明我们编写的程序确实收敛到了最优解.