1 描述性统计分析方法
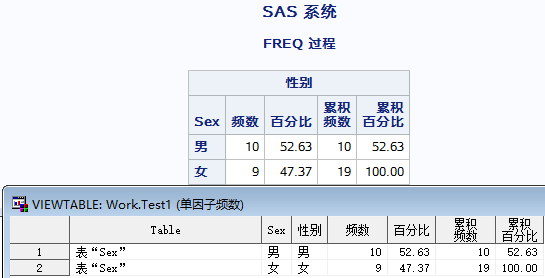
定性资料常用描述性统计分析为频数、频率,通常使用 PROC FREQ 过程→ tables 语句:
ods output OneWayFreqs=Test1;/*导出输出结果到test1数据集*/
proc freq data=sashelp.class;
tables sex;/*sex为分类变量,取值为男/女*/
run;
ods output close;
结果如下:
2 单组样本
2.1 二项分布
二项分布(binomial distribution)是指在只会产生两种可能结果如“阳性”或“阴性”之一的 \(n\) 次独立重复试验中,当每次试验的“阳性”概率 \(\pi\) 保持不变时,出现“阳性”次数 \(X\ =\ 0,1,2,...,n\) 的一种概率分布。其概率可由下面的公式求出:
[!INFO] 二项分布的适用条件为:
- 每次试验只会发生两种对立的可能结果之一,即分别发生两种结果的概率之和恒等于1。
- 每次试验产生某种结果(如“阳性”)的概率 \(\pi\) 固定不变。
- 重复试验是相互独立的,即任何一次试验结果的出现不会影响其他试验结果出现的概率。
利用二项分布及其正态近似性,可进行总体率的区间估计和差异推断。当 \(n\) 较大, \(\pi\) 或 \((1-\pi)\) 不接近0,也不接近1时,二项分布 \(B(n,\pi)\) 近似正态分布 \(N(n\pi,n\pi(1-\pi))\) ,而对应的样本率 \(p\) 也近似正态分布 \(N(\pi,\sigma_p^2)\) 。
2.1.1 求总体率的置信区间
当 \(n\) 较大, \(p\) 和 \(1-p\) 均不太小,如 \(np\) 和 \(n(1-p)\) 均大于5时,可利用样本率 \(p\) 的分布近似正态分布来估计总体率的 \(1-\alpha\) 可信区间。计算公式为:
[!example] 示例
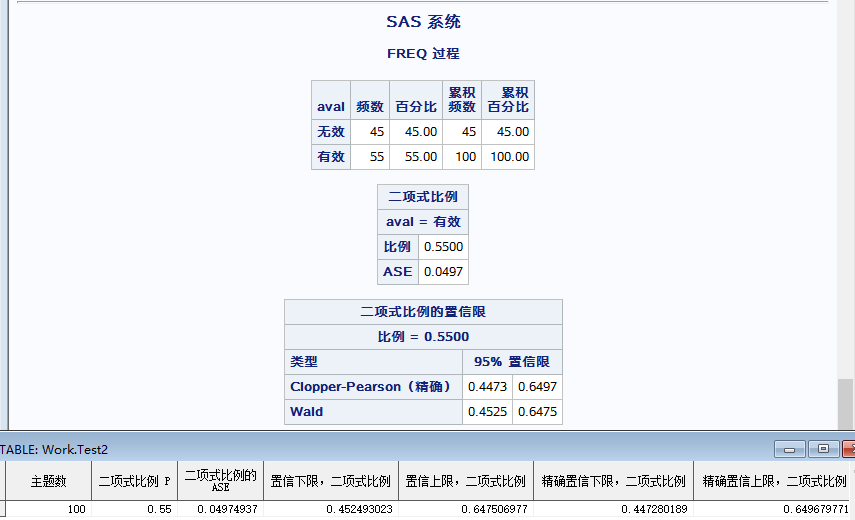
例2-1 在观测一种药物对某种非传染性疾病的治疗效果时,用该药治疗了此种非传染性疾病患者100人,发现55人有效,试据此估计该药物治疗有效率的95%可信区间。
使用 PROC FREQ → tables 语句 → binomial 参数:
data tmp1;/*构建数据集*/
aval = "无效"; count = 45; output;
aval = "有效"; count = 55; output;
run;
proc freq data = tmp1;
tables aval/ alpha=0.05 binomial (level="有效" cl=wald exact);
/*alpa=0.05:指定生成95%置信区间(alpha默认值为0.05);
level="有效":指定要计算置信区间的率的水平;
cl=wald exact:指定置信区间的计算方法(cl取值有多种,具体可参见SAS帮助文档)*/
weight count;
output out=test2 binomial;/*导出binomial输出结果到test2数据集*/
run;
结果如下:
2.1.2 样本率与总体率的比较
当 \(n\) 较大, \(p\) 和 \(1-p\) 均不太小,如 \(np\) 和 \(n(1-p)\) 均大于5时,利用样本率的分布近似正态分布的原理,可作样本所在的总体率 \(\pi\) 与已知总体率 \(\pi_0\) 的比较。检验统计量 \(u\) 值得计算公式为:
[!example] 示例
例2-2 已知某疾病采用常规治疗的治愈率为45%。现随机抽取180名该疾病患者改用新的治疗方法进行治疗,治愈117人。问新治疗方法是否比常规疗法的效果好?本例是单侧检验,记新治疗方法的治愈率为 \(\pi\) ,而 \(\pi_0=0.45\) 。其假设检验为:
\[\begin{align} &H_0:\ \pi=0.45 \\ &H_1:\ \pi\ne0.45 \end{align}\]
使用 PROC FREQ → tables 语句 → binomial 参数:
data tmp1;/*构建数据集*/
aval = "未治愈"; count = 63; output;
aval = "治愈"; count = 117; output;
run;
proc freq data = tmp1;
tables aval/ alpha=0.05 binomial (level="治愈" p=0.45 cl=wald exact);
/*alpa=0.05:指定生成95%置信区间(alpha默认值为0.05);
level="治愈":指定要计算置信区间的率的水平;
p=0.45:指定要与之比较的总体率,取值可为0-1或0-100(百分比形式);
cl=wald exact:指定置信区间的计算方法(cl取值有多种,具体可参见SAS帮助文档)*/
weight count;
output out=test3 binomial;
run;
结果如下:

2.2 Poisson分布
Poisson 分布(Poisson distribution)作为二项分布的一种极限情况,已发展成为描述小概率事件发生规律的一种重要分布。它可用来分析医学上诸如人群中遗传缺陷、癌症等发病率很低的非传染性疾病的发病或患病人数的分布,也可用于研究单位时间内(或单位面积、容积、空间内)某罕见事件发生次数的分布,如分析在单位时间内放射性物质放射次数的分布,在单位面积或容积内细菌数的分布,在单位空间中某种昆虫或野生动物数的分布等。随机变量 \(X\) 服从 Poisson 分布,是指在足够多的 \(n\) 次独立试验中, \(X\) 取值为 \(0,1,2...,\) 的相应概率为:
式中参数 \(\lambda\) 即为总体均数, \(e=2.71828\) 为一常数。且有 \(\Sigma P(X)=1\) 。 \(X\) 服从以 \(\lambda\) 为参数的 Poisson 分布,记作 \(X\)~\(P(\lambda)\) 。
[!INFO] Poisson分布的适用条件
假定在规定的观测单位内某事件(如“阳性”)平均发生次数为 \(\lambda\) ,且该规定的观测单位可等分为充分多的 \(n\) 份,其样本计数为 \(X(X=0,1,2,...)\) 。则在满足下面三个条件时,有 \(X\)~\(P(X)\) 。
- 普通性:在充分小的观测单位上 \(X\) 的取值最多为1。
- 独立增量性:在某个观测单位上 \(X\) 的取值与前面各观测单位上的 \(X\) 的取值无关。
- 平稳性: \(X\) 的取值只与观测单位的大小有关,而与观测单位的位置无关。
[!INFO] Poisson分布的性质
- 总体均数 \(\lambda\) 与总体方差 \(\sigma^2\) 相等是 Poisson 分布的重要特征。
- 当 \(n\) 很大,而 \(\pi\) 很小,且 \(n\pi=\lambda\) 为常数时,二项分布近似 Poisson 分布。
- 当 \(\lambda\) 增大时,Poisson 分布渐进正态分布。一般而言,\(\lambda\) ≥20 时,Poisson 分布资料可作为正态分布处理。
2.2.1 求总体率的置信区间
对于获得的样本计数 \(X\),当 \(X\) > 50 时,可采用正态近似法估计总体均数的 \(1-\alpha\) 可信区间,计算公式为:
其中 \(u_{\alpha/2}\) 为标准正态分布分位数(SAS PROBIT 函数为左侧分位数)。SAS中分位数函数可参考【新手必备】SAS常用函数整理 - 知乎 (zhihu.com)。
[!example] 示例
例2-3 某研究者对某社区12000名居民进行了健康检查,发现其中有68名胃癌患者。估计该社区胃癌患病数的95%可信区间。
可根据公式进行编程:
data a;
X=68;/*X计数=68*/
alpha=0.05;/*alpha取值为0.05*/
LowerCL=X-probit(0.975)*sqrt(X);/*置信区间下限*/
UpperCL=X+probit(0.975)*sqrt(X);/*置信区间上限*/
run;
结果如下:

2.2.2 样本均数与总体均数的比较
根据 Poisson 分布的性质,当 \(\lambda\) ≥ 20 时,可用正态近似法来近似。样本计数 \(X\) 与已知总体均数 \(\lambda\) 的比较,检验统计量 \(u\) 的计算公式为:
[!example] 示例
例2-4 有研究表明,一般人群精神发育不全的发生率为3‰,今调查了有亲缘血统婚配关系的后代25000人,发现123人精神发育不全,问有亲缘血统婚配关系的后代其精神发育不全的发生率是否要高于一般人群?可认为人群中精神发育不全的发生数服从 Poisson 分布。本例 \(n\)=25000,\(X=123\) , \(\pi_0\)=0.003 , \(\lambda=n\pi_0\) =25000×0.003=75。假设检验为:
\[\begin{align} &H_0:\ \pi=0.003 \\ &H_1:\ \pi\ne0.003 \end{align}\]
可根据公式进行编程:
data b;
n=25000;
X=123;
pi_0=0.003;
lambda=n*pi_0;
alpha=0.05;
u=(X-lambda)/sqrt(lambda);/*求u值*/
P=1-probnorm(u);/*且u对应的P值*/
run;
结果如下:
