思路
区间dp。
设状态 $f_{l,r}$ 为在区间 $[l,r]$ 内要放的最少保镖数量。
看到题面第一眼的感觉是不会判两点能否连接。
第二眼发现可以用斜率判。
令 $k_{l,r}$ 为横坐标为 $l,r$ 的两点连线斜率。
有 $k_{l,r}=\frac{h_r-h_l}{r-l}$。
手搓几组样例,得 $\forall x\in[l,r)$,有 $k_{l,r}<k_{x,r}$ 。即对于 $x\in[l,r)$,$(x,r)$ 的连线斜率最小。
且若 $a$ 对于 $b$ 可见,且 $h_c>h_b,c>a$,则 $a$ 对于 $c$ 可见。
令 $p={p_1,p_2\cdots p_m}$ 为 $r$ 点当前能够覆盖的点集。注:下文中 $p$ 按照从右至左斜率单调递减的顺序排序。
注:能被覆盖的点可能不连续。但能被覆盖的点的斜率可以保证从右至左单调递减。
若想为点集连续,可能会导致 “$p$ 为 $r$ 点当前能够覆盖的最远点” 的错误贪心思路。
喜提20pt。
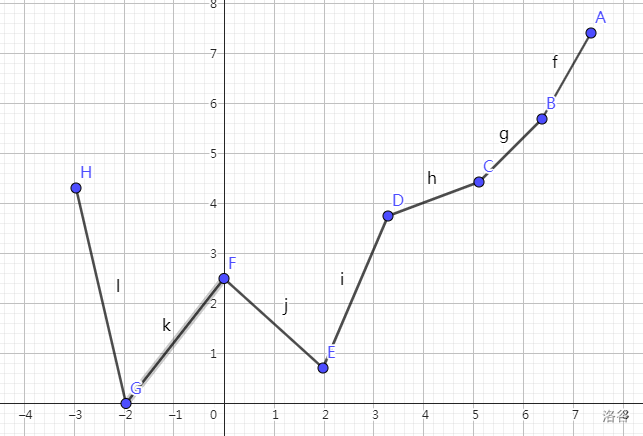
如图,$r=G$ 时,$p={E,D,B}$。
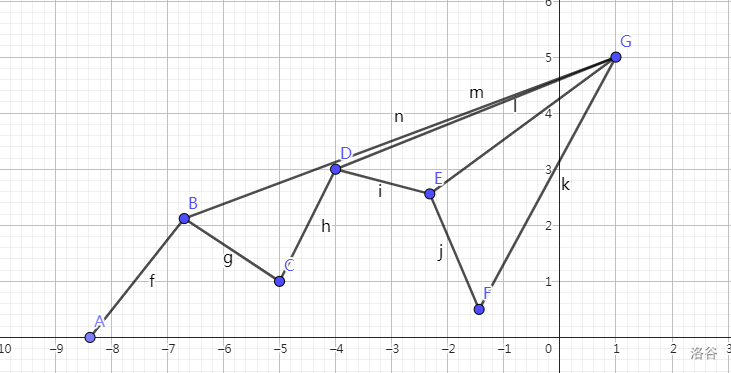
接下来是这题个人认为比较难处理的地方。
由于 $p$ 不一定连续,故 $[p_{i+1}+1,p_i-1]$ 对于 $r$ 不可见。
由上述性质得,对于 $j\in[p_i,r)$,$j=p_i$ 是唯一可以覆盖 $[p_{i+1}+1,p_i-1]$ 中至少一个点的点。 即在区间 $(p_{i+1},p_i)$ 右侧唯一能够覆盖到此区间的点为 $p_i$。(有点绕,建议自己手玩一下。)
如图,以 $A$ 为右端点,$[D,A]$ 中能覆盖 $[G,E]$ 的唯一点为 $D$。
当然,也可以选择在 $p_i-1$ 处放置保镖,从内部将点覆盖。
如在点 $E$ 放置保镖。
故 $p_i,p_i-1$ 至少有一处要放置保镖。
这样就成功的将区间 $[p_{i+1}+1,p_i]$ 或 $[p_{i+1}+1,p_i-1]$ 转换为了一个子问题。
区间 $[p_{k+1}+1,p_k-1]$ 的代价即为 $$f_{p_{i+1}+1,p_i-1}=\min{f_{p_{i+1}+1,p_i-1},f_{p_{i+1}+1,p_i}}$$
此时有转移方程:
$$f_{l,r}=\sum\limits_{i=1}^m\min{f_{p_{i+1}+1,p_i-1},f_{p_{i+1}+1,p_i}}$$
时间复杂度 $O(n^3)$,能拿 $70$ pts。
考虑优化。
-
因为 $p_i$ 是在 $[p_i,r)$ 中与 $r$ 点连线斜率最小的,所以对于$x\in[l,p_i)$,若存在 $f_{x,r}<f_{p_i,r}$,则 $p_{i+1}=x$。 可以考虑将 $p_i$ 在循环里滚动处理。
-
可以注意到根据上述转移,当处理至 $p$ 点时,区间 $[p,r]$ 可以保证被完全覆盖。有转移方程
$$f_{l,r}=\min{f_{l,p-1,f_{l,p}}}+f_{p+1,r}$$
干掉一个线性时间复杂度。时间复杂度 $O(n^2)$。
具体实现上有问题的话可以看代码。
#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define eps 1.0000
typedef long long ll;
const int maxn = 5020;
const ll inf = 1e18;
int n;
int h[maxn];
ll f[maxn][maxn], res;
bool check(int a, int b, int p){
double ka = (h[p] - h[a]) * eps / (p - a);
double kb = (h[p] - h[b]) * eps / (p - b);
return ka < kb;
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &h[i]), f[i][i] = 1;
for(int r = 1; r <= n; r++){
int pos = -1;
for(int l = r - 1; l >= 1; l--){
if(pos == -1 || check(l, pos, r)) pos = l;
f[l][r] = std::min(f[l][pos - 1], f[l][pos]) + f[pos + 1][r];
}
}
for(int i = 1; i <= n; i++)
for(int j = i; j <= n; j++)
res ^= f[i][j];
printf("%lld", res);
return 0;
}
初二婴儿,轻喷 qwq
我觉得这篇题解应该是题解区比较详细的?