一、换根树形动态规划
换根树形动态规划又称二次扫描,相较于一般的树形动态规划,有如下特点:
- 以树上不同的节点为根,其解不同
- 求解答案时,不能只求解某一点的信息,而是求解所有点的信息
- 无法通过一次搜索来求解答案
二、例题
1.[Daimayuan Online Judge.距离和]
题目描述
有一棵 \(n\) 个节点的树,节点编号从 \(1\) 到 \(n\)。请求出每个节点到其他所有节点的距离的和。
定义两个节点的距离为它们之间的简单路径上经过了多少条边。
输入格式
第一行一个整数 \(n\) 表示节点数。
接下来 \(n−1\) 行,每行两个整数 \(x,y\) 表示 \(x\) 号节点和 \(y\) 号节点之间有一条边。
数据保证读入的是一棵树。
输出格式
输出共 \(n\) 行,第 \(i\) 行一个整数表示 \(i\) 号节点到其他所有节点的距离的和。
数据范围
对于所有数据,保证 \(2≤n≤10^5,1≤x,y≤n\)。
输入样例
5
1 2
1 5
2 3
2 4
输出样例
6
5
8
8
9
解题思路
考虑以 \(1\) 为根的有根树的情况,用 \(size_i\) 表示以 \(i\) 为根的子树中有多少个点,\(f_i\) 表示考虑以 \(i\) 为根的子树,\(i\) 到子树中其他所有点的距离和。
\(size_i\) 很好计算,考虑 \(j\) 为 \(i\) 的直接子节点,\(size_i=(\sum size_j)+1\)。
\(f_i\) 如何计算?考虑考虑 \(j\) 为 \(i\) 的直接子节点,以 \(j\) 为根的子树对 \(f_i\) 的贡献为 \(f_j+size_j\),则 \(f_i=\sum(f_j+size_j)=\sum f_j+\sum size_j=\sum f_j+size_i-1\)。
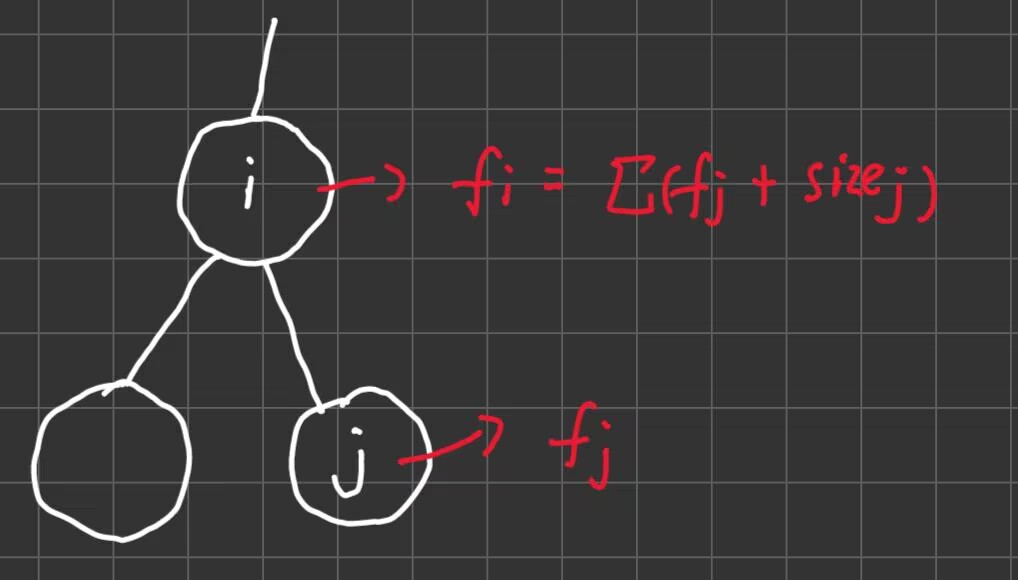
加上 \(size_j\) 是因为节点 \(j\) 到 \(i\) 的距离为 \(1\),而 \(j\) 子树的每个点到 \(i\) 要经过 \(j\),都需要加 \(1\),恰好为 \(size_j\)。
当根从 \(1\) 变为其子节点 \(i\) 会怎么样?
除了 \(1\) 为根时考虑的子树(贡献值为 \(f_i\)),多了一个以 \(1\) 为根的子树,这个贡献值如何求解,要求解的部分如图所示?
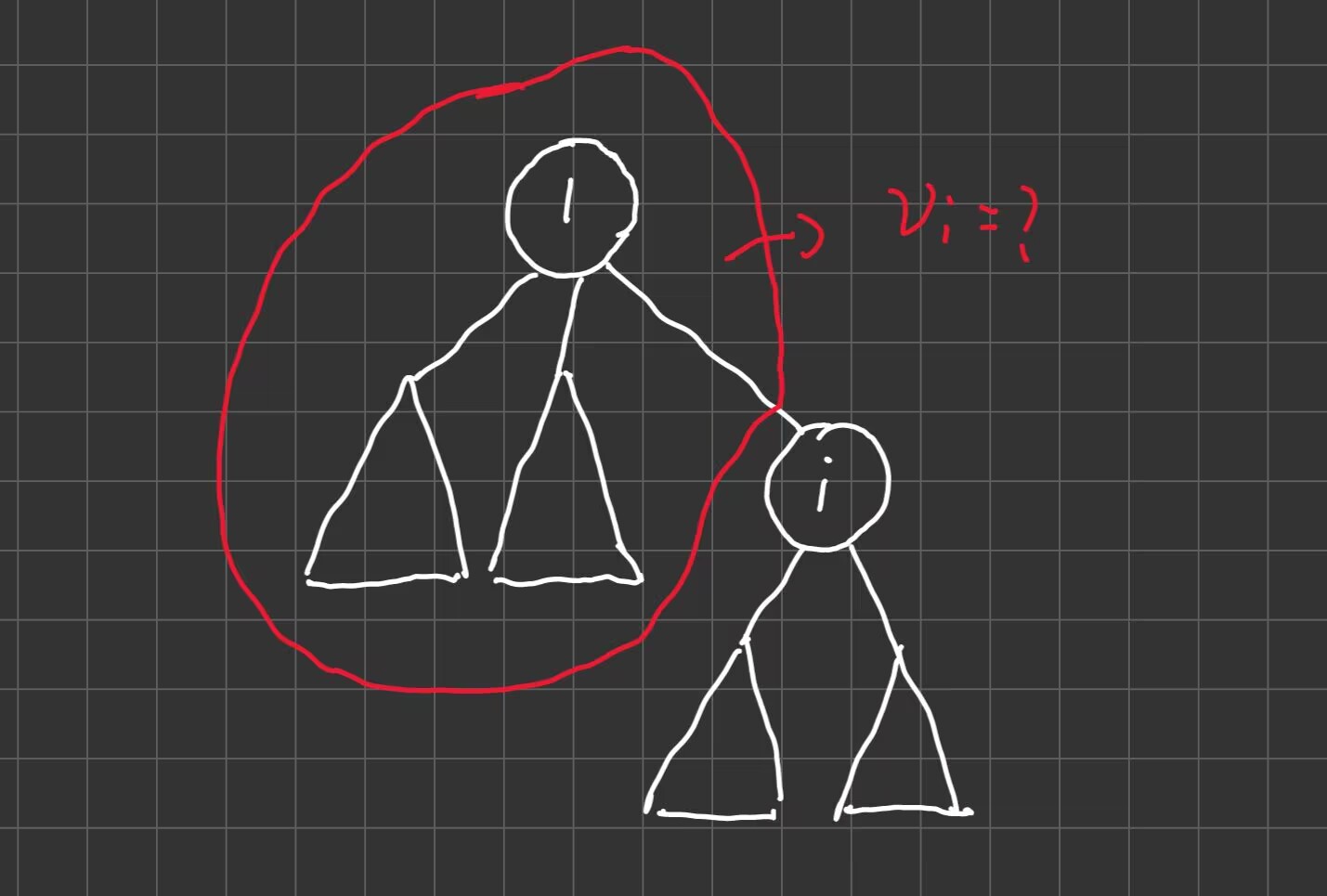
用 \(v_i\) 表示一个点的父亲作为其子树时的贡献值,\(v_1=0\),\(v_i=(f_1-f_i-size_i)+(n-size_i)\),即求解 \(v_i\),从总的 \(v_1+f_1\) 中去除以 \(i\) 为子树的贡献值 \(f_i\) 以及相连的那条边的贡献 \(size_i\),然后加上以 \(1\) 为子树的每个点经过 \(1\) 到 \(i\) 的贡献,即以 \(1\) 为根的子树的节点数 \(n-size_i\)。
当根从 \(x\) 变成其子节点 \(y\) 会怎么样?
除了 \(1\) 为根时考虑的子树(贡献值为 \(f_y\)),多了一个以 \(x\) 为根的子树,这个贡献值如何求解?
类似上面的思路,\(v_y=(v_x+f_x-f_y-size_y)+n-size_y\)。首先对于 \(x\) 来说,其总的距离和为 \(v_x+f_x\),而去除以 \(y\) 为根的子树的贡献值以及子树节点经 \(y\) 到 \(x\) 相连的边的贡献值 \(f_y+size_y\) 即可得到以 \(x\) 为根的子树的贡献值,再加上子树节点经 \(x\) 到 \(y\) 相连边的贡献值 \(n-size_y\)。
对于任意的 \(y\),以 \(y\) 为根时的答案为 \(v_y+f_y\)。
C++代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 200010;
typedef long long LL;
int n;
int h[N], e[M], ne[M], idx;
int size[N];
LL f[N], v[N];
bool b[N];
void add(int x, int y) {
e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
void up(int u) {
size[u] = 1;
b[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
if (!b[e[i]]) {
up(e[i]);
size[u] += size[e[i]];
f[u] += f[e[i]];
}
}
f[u] += size[u] - 1;
}
void down(int u) {
b[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
if (!b[e[i]]) {
v[e[i]] = v[u] + f[u] - f[e[i]] - size[e[i]] + n - size[e[i]];
down(e[i]);
}
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
memset(b, false, sizeof b);
up(1);
memset(b, false, sizeof b);
down(1);
for (int i = 1; i <= n; i++)
printf("%lld\n", f[i] + v[i]);
return 0;
}
2.[Daimayuan Online Judge.流]
题目描述
有一棵 \(n\) 个节点的树,节点编号从 \(1\) 到 \(n\),树上的每条边都有流量限制。令某一个节点为根节点,向这个节点灌水,最终从叶子节点流出的水量之和为这个节点的最大流量。请求出每个节点的最大流量。
输入格式
第一行一个整数 \(n\) 表示节点数。
接下来 \(n−1\) 行,每行三个整数 \(x,y,z\) 表示 \(x\) 号节点和 \(y\) 号节点之间有一条流量限制为 \(z\) 的边。
数据保证读入的是一棵树。
输出格式
输出共 \(n\) 行,第 \(i\) 行一个整数表示 \(i\) 号节点的最大流量。
数据范围
对于所有数据,保证 \(2≤n≤10^5,1≤x,y≤n,1≤z≤10^9\)。
输入样例
5
1 2 3
1 5 1
2 3 2
2 4 2
输出样例
4
5
2
2
1
解题思路
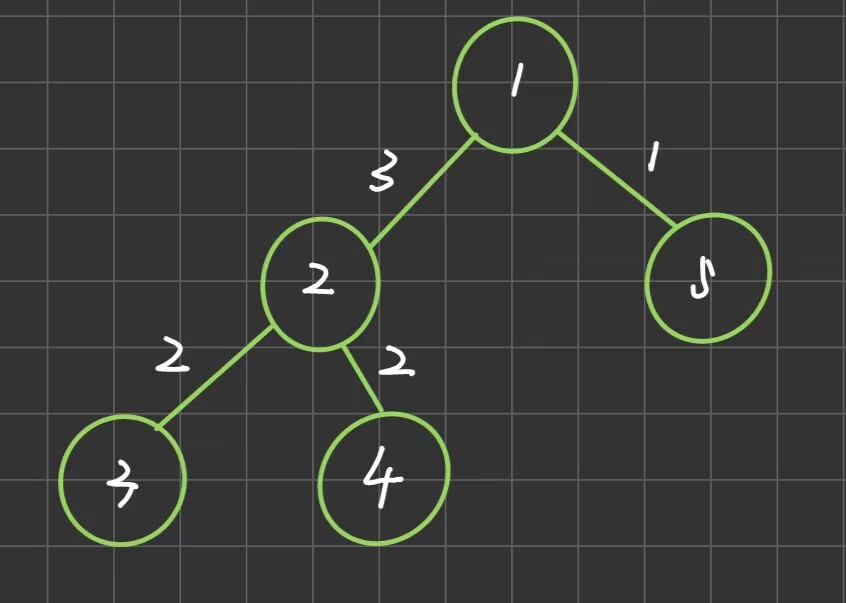
以输入样例为例,以 \(1\) 为根流入,其他点流出的最大流量为 \(1+3=4\),虽然 \(2-3\) 和 \(2-4\) 都为 \(2\) 但是 \(1-2\) 为 \(3\) 会限制流量,其他类似,比如以 \(2\) 为根流入,最后流出的为 \(2+2+1=5\)。
先考虑以 \(1\) 为根(也就是从 \(1\) 灌水)的有根树的情况,\(f_i\) 表示以 \(i\) 为根的子树,最多可以承接多少来自上面的流量,那么 \(f_i\) 如何计算?
假设 \(j\) 是 \(i\) 的儿子,以 \(j\) 为根的子树对 \(f_i\) 的贡献值为 \(min(c_j, f_j)\),其中 \(c_j\) 表示从 \(j\) 到 \(i\) 的边的流量限制,则 \(f_i=\sum min(c_j,f_j)\),另外如果 \(j\) 为叶子节点,其理论上可以流出无限流量,但其会受 \(c_j\) 也就是 \(i\) 到 \(j\) 的边的限制。
当根从 \(1\) 变成它的儿子 \(i\) 时会发生什么?
除了 \(1\) 为根时考虑的子树(贡献值为 \(f_i\)),多了一个以 \(1\) 为根的子树,后面这个贡献值如何求解?
用 \(v_i\) 表示一个点的父亲作为其子树时的贡献(以 \(i\) 的父节点为根的子树最多可以承接的流量),则 \(v_i=min(v_1+f_1-min(c_i,f_i),c_i)\),即首先去除以 \(i\) 为根的子树的流量贡献值即为以 \(1\) 为根的可承接流量,再和 \(c_i\) 取最小值限制。
注意,这里还有一种特殊情况,把根从父亲 \(1\) 号点换成儿子 \(i\) 号点后 \(1\) 号点有可能会成为新的叶子节点,这时候新的以 \(1\) 为根的子树最多可以承接的流量为无限大,所以最多有多少流量可以从 \(i\) 号点流到这颗子树只会被 \(c_i\) 限制,也就是说这时的 \(v_i=c_i\),否则 \(v_1=0\)。
当根从 \(x\) 变成它的儿子 \(y\) 的时候会发生什么?
除了 \(1\) 为根时考虑的子树(贡献值为 \(f_y\)),多了一个以 \(x\) 为根的子树,后面这个贡献值如何求解?
\(v_y=min(v_x+f_x-min(c_y,f_y),c_y)\),对于 \(y\),以其为根时的答案就是 \(v_y+f_y\)。
C++代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 200010;
typedef long long LL;
int n;
int h[N], e[M], w[M], ne[M], idx;
LL f[N], v[N];
bool b[N];
void add(int x, int y, int z) {
e[idx] = y, w[idx] = z, ne[idx] = h[x], h[x] = idx++;
}
void up(int u) {
b[u] = true;
bool flag = true;
for (int i = h[u]; ~i; i = ne[i]) {
if (!b[e[i]]) {
up(e[i]);
f[u] += min(1LL * w[i], f[e[i]]);
flag = false;
}
}
if (flag)
f[u] = 1 << 30; // 叶子节点不考虑父节点流量为无限大
}
void down(int u) {
b[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
if (!b[e[i]]) {
if (v[u] + f[u] - min(1LL * w[i], f[e[i]]))
v[e[i]] = min(v[u] + f[u] - min(1LL * w[i], f[e[i]]), 1LL * w[i]);
else // 所有流量从u到j,则变换根为j,u为叶子节点
v[e[i]] = w[i];
down(e[i]);
}
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
add(x, y, z);
add(y, x, z);
}
memset(b, false, sizeof b);
up(1);
memset(b, false, sizeof b);
down(1);
for (int i = 1; i <= n; i++)
if (f[i] != 1 << 30)
printf("%lld\n", f[i] + v[i]);
else
printf("%lld\n", v[i]);
return 0;
}
3.[Daimayuan Online Judge.最长路径]
题目描述
有一棵 \(n\) 个节点的树,节点编号从 \(1\) 到 \(n\)。对于每个节点,请求出经过它的长度最长的简单路径有多长。
定义一条路径的长度为这条路径上经过了多少条边。
输入格式
第一行一个整数 \(n\) 表示节点数。
接下来 \(n−1\) 行,每行两个整数 \(x,y\) 表示 \(x\) 号节点和 \(y\) 号节点之间有一条边。
数据保证读入的是一棵树。
输出格式
输出共 \(n\) 行,第 \(i\) 行一个整数表示经过 \(i\) 号节点的长度最长的简单路径有多长。
数据范围
对于所有数据,保证 \(2≤n≤10^5,1≤x,y≤n\)。
输入样例
5
1 2
1 5
2 3
2 4
输出样例
3
3
3
3
3
解题思路
基本思路同前两道题。
首先考虑以 \(1\) 为根,则经过 \(1\) 的长度最长的简单路径长度为其到子节点的最长的两个路径之和。那么定义三维数组 \(f\),第一维表示当前节点,第二维表示最长和次长的两个路径,第三维表示路径长度和途径的节点。
这里 \(f\) 的求解可以当做求解以 \(1\) 为根的树维护每个节点两个最大的深度。
随后定义一维数组 \(v\),\(v_i\) 表示 \(i\) 的父节点(以 \(1\) 为根的情况下)维护的路径最大长度。根从 \(1\) 变成其子节点 \(i\),求解 \(v_i\) 需要考虑 \(1\) 维护的最长路径是否经过 \(i\)。然后推广到 \(x\) 的子节点 \(y\)。
答案为每个节点 \(f[i][0][0],f[i][1][0],v[i]\) 三个值中最大的两个值的和。
C++代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 200010;
typedef long long LL;
int n;
int h[N], e[M], ne[M], idx;
int f[N][2][2], v[N]; // f[i][0]表示最长的路径,f[i][1]表示次长路径,f[i][][0]表示路径长度,f[i][][1]表示经过的子节点
bool b[N];
void add(int x, int y) {
e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
void up(int u) {
b[u] = true;
bool flag = true;
for (int i = h[u]; ~i; i = ne[i]) {
if (!b[e[i]]) {
up(e[i]);
if (f[e[i]][0][0] + 1 > f[u][0][0]) { // 子节点的最长路径+1大于父节点的最长路径
f[u][1][0] = f[u][0][0]; // 次长路径更新
f[u][1][1] = f[u][0][1];
f[u][0][0] = f[e[i]][0][0] + 1;
f[u][0][1] = e[i];
} else {
if (f[e[i]][0][0] + 1 > f[u][1][0]) //节点的最长路径+1大于父节点的次长路径
f[u][1][0] = f[e[i]][0][0] + 1;
f[u][1][1] = e[i];
}
}
}
}
void down(int u) {
b[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
if (!b[e[i]]) {
if (f[u][0][1] == e[i]) { // 父节点最长路径经过当前子节点
if (v[u] > f[u][1][0])
v[e[i]] = v[u] + 1;
else
v[e[i]] = f[u][1][0] + 1;
} else {
v[e[i]] = max(f[u][0][0], v[u]) + 1;
}
down(e[i]);
}
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
memset(b, false, sizeof b);
up(1);
memset(b, false, sizeof b);
down(1);
for (int i = 1; i <= n; i++)
printf("%d\n", f[i][0][0] + f[i][1][0] + v[i] - min(min(f[i][0][0], f[i][1][0]), v[i]));
return 0;
}