A 反转Dag图 :
题面
给出一个 \(n\) 个点 \(m\) 条边的有向图,顶点编号 \(1\) 到 \(n\) ,边的编号为 \(1\) 到 \(m\) 。
你可以选择一些边进行反转(即从 \(u\) 到 \(v\) 的边反转后变为从 \(v\) 到 \(u\) 的边),将每条边反转都需要一定代价。最终使得整个图变成一个 \(Dag\) 图。
总的反转代价是由所有需要反转的边中,代价最高的那一条决定的,求达成目标的最小代价。
对于 \(100\%\) 的数据,\(2\le n\le10^5\) ,\(1\le m\le10^5\),$1\le c \le 10^9 $。
样例输入
5 6
2 1 1
5 2 6
2 3 2
3 4 3
4 5 5
1 5 4
样例输出
2
分析
这道题考试时候傻逼了,都已经想到正解了,不知道怎么被自己给否定了。
这道题要使最大边权最小,那么很容易想到二分这个最大边权,然后怎么做呢?我一开始想的是将边权小于这个二分值的边直接反转,这样肯定是错的,我举了个反例就否定了这个做法,现在只想骂自己傻逼。
其实对于边权小于二分值的边,怎么样反转都是可行的,我一直以为只能翻转一次,所以就错了,所以那些小的边绝对不会成为环的边,如果在环上,直接反转就行了,所以只要将大于二分值的边加进去,用tarjan判断是否有环就行了,(其实拓扑也行,只是我没想到)。
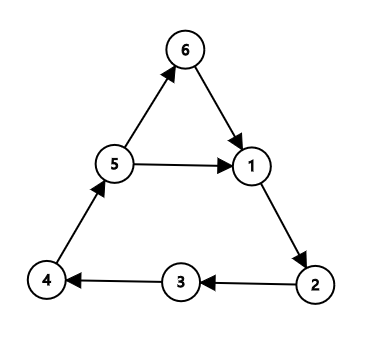
可能会有些疑惑,如果那些小边反转后成为另一个环的边怎么办呢?
其实没事,可以看下图,发现如果小边(5,1)翻不翻转都不会有什么影响,因为有一个大的环,所以大的环上也要有边反转。
\(code\)
#include<bits/stdc++.h>
#define N 1000005
#define INF 0x3f3f3f3f
using namespace std;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
int n,m,tot,t,cnt,top;
int Head[N],to[N],Next[N];
int s[N],vis[N],dfn[N],low[N];
void add(int u,int v){
to[++tot]=v,Next[tot]=Head[u],Head[u]=tot;
}
struct EDGE{
int u,v,w;
}a[N];
void tarjan(int x){
dfn[x]=low[x]=++t,s[++top]=x,vis[x]=1;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(!dfn[y]) tarjan(y),low[x]=min(low[x],low[y]);
else if(vis[y]) low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x]){
cnt++;int k=-1;
while(k!=x){
k=s[top--];vis[k]=0;
}
}
}
void init(){
tot=0,cnt=0,t=0,top=0;
memset(Head,0,sizeof(Head));
memset(dfn,0,sizeof(dfn)),memset(low,0,sizeof(low));
}
bool check(int x){
init();
for(int i=1;i<=m;++i) if(a[i].w>x) add(a[i].u,a[i].v);
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
return cnt==n;
}
int main(){
n=read(),m=read();
for(int i=1;i<=m;++i) a[i].u=read(),a[i].v=read(),a[i].w=read();
int l=0,r=1e9,ans=0;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
printf("%d\n",ans);
return 0;
}
B 歪脖子树 :
题面
杭州有一棵 \(n\) 个点的歪脖子树(节点编号 \(1\sim n\)),每个点有一个丑陋度 \(a[i]\)。
它的长相过于奇怪以至于人们甚至不知道它的根在哪里,但大家初始时都假定节点 \(1\) 为根。
为了验证,植物学家们做了 \(T\) 次实验,每次实验形如下列三者之一:
V x y:把点 \(x\) 的丑陋度改成 \(y\) ;
E x:将 \(x\) 设为新的树根;
Q x:查询 \(x\) 的子树中丑陋度的最小值;
对于 \(100\%\) 的数据, \(2\le n \le 10^5\),\(1\le T\le 10^5\),\(0\le v\le 10^4\)。
输入样例
3 7
0 1
1 2
1 3
Q 1
V 1 6
Q 1
V 2 5
Q 1
V 3 4
Q 1
输出样例
1
2
3
4
分析
一道关于 dfs 序的题,其实不用去考虑换根的事情,在仍旧以 1 为根的情况下也能做到。
如果不会换根,显然可以用 dfs 序 + 线段树来求解,因为子树的dfs 必定是连续,可以转化为线段树单点修改,区间查询,那会修改根呢?。
一个显然的性质:如果换了根,那么只有 1 到 root 这条路径上的点的答案会改变,所以我们可以特判一下这种情况,如果一个点不在 1 到 root 的路径上,就仍旧以 以 1 为根的答案为答案。
那如果在这条路径上,显然 root 答案为 \(1\sim n\) 整段区间的答案,其余点的答案为 \(1\sim n\) 整段区间 的减去 有 root 的子树的区间,显然 以 root 的子树是一段连续的区间,那么答案就是不带这个区间的两段区间。
\(code\)
#include<bits/stdc++.h>
#define N 100005
#define ls u<<1
#define rs u<<1|1
using namespace std;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
int n,T,tot,t,root=1;
int a[N],dfn[N],d[N],gp[N],f[N][25];
int Head[N],to[N<<1],Next[N<<1];
int minn[N<<2],siz[N],val[N];
void add(int u,int v){
to[++tot]=v,Next[tot]=Head[u],Head[u]=tot;
}
void PushUp(int u){
minn[u]=min(minn[ls],minn[rs]);
}
void dfs(int x,int fa){
d[x]=d[fa]+1,f[x][0]=fa;
dfn[x]=++t;siz[x]=1,val[t]=a[x];
for(int i=Head[x];i;i=Next[i]){
int y=to[i];if(y==fa) continue;
dfs(y,x);siz[x]+=siz[y];
}
}
void Build(int u,int l,int r){
if(l>=r){minn[u]=val[l];return ;}
int mid=(l+r)>>1;
Build(ls,l,mid);
Build(rs,mid+1,r);
PushUp(u);
}
void UpDate(int u,int l,int r,int x,int k){
if(l==r){minn[u]=k;return ;}
int mid=(l+r)>>1;
if(x<=mid) UpDate(ls,l,mid,x,k);
else UpDate(rs,mid+1,r,x,k);
PushUp(u);
}
int Query(int u,int l,int r,int L,int R){
if(R<L) return 1e9; //边界处理
if(L<=l&&r<=R) return minn[u];
int mid=(l+r)>>1,ans=1e9;
if(L<=mid) ans=min(ans,Query(ls,l,mid,L,R));
if(R>mid) ans=min(ans,Query(rs,mid+1,r,L,R));
return ans;
}
int lca(int x,int y){
if(d[x]>d[y]) swap(x,y);
for(int j=20;j>=0;--j) if(d[f[y][j]]>d[x]) y=f[y][j];
if(f[y][0]==x) return y;
return 0;
}
int main(){
n=read(),T=read();
for(int i=1;i<=n;++i){
int x=read();a[i]=read();
if(x!=0) add(x,i),add(i,x);
}
dfs(1,0);
for(int j=1;j<=20;++j)
for(int i=1;i<=n;++i)
f[i][j]=f[f[i][j-1]][j-1];
Build(1,1,n);
while(T--){
char opt[2];
int x,y;
scanf("%s",opt+1);x=read();
if(opt[1]=='V'){
y=read();a[x]=y;
UpDate(1,1,n,dfn[x],y);
}else if(opt[1]=='E'){
root=x;
}else{
if(root==x){printf("%d\n",minn[1]);continue;}
int tt=lca(x,root);
if(d[x]<d[root]&&tt) printf("%d\n",min(Query(1,1,n,1,dfn[tt]-1),Query(1,1,n,dfn[tt]+siz[tt],n)));
else printf("%d\n",Query(1,1,n,dfn[x],dfn[x]+siz[x]-1));
}
}
return 0;
}
C 倒水问题 :
有 \(n\) 个水杯,水杯中分别有 \(a[i]\) 升水,你采用以下方式把所有水杯倒空。
设当前所有水杯中水量最多的一杯有 \(g\) 升,你可以把所有水量在 \(g/2\) (下取整)以上的水杯都倒空。
然后继续这个操作,直到所有水杯被倒空为止。设总共倒了 \(h\) 次。 不过在干这个事情之前,你可以先选出至多 \(k\) 个水杯,预先将其中的水都倒空。
你可以通过不同的选择,让最终的 \(h\) 尽可能小。问最小的 \(h\) 是多少,同时输出预先倒空的水杯数量(有可能小于 \(k\))?
对于 \(100\%\) 的数据,\(1\le n\le 2×10^5\),\(0\le k\le n\),\(1\le a_i \le 10^9\)
输入样例
4 1
2 3 4 9
输出样例
2 1
分析
没想到居然是 dp,我还以为是贪心什么之类的,好吧,可能贪心贪不到最优解。
设 \(f_{i,j}\) 表示倒到 第 \(i\) 杯水(第 \(i\) 杯水也被倒了),倒了 j 组水,用了 \(f_{i,j}\) 的事先倒水次数,考虑转移方程:
其中,\(t\) 是小于等于 \(\dfrac{a_i}{2}\) 的数的最大下标,因为值域不超过 1e9 ,所以 j 最多为 32,所以复杂度 \(O(32n)\),\(t\) 可以预处理出来。最后答案显而易见。
#include<bits/stdc++.h>
#define N 200005
using namespace std;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
int n,k;
int a[N],f[N][35],b[N];
int main(){
n=read(),k=read();
for(int i=1;i<=n;++i) a[i]=read();
if(n==k) return printf("0 %d\n",k),0;
sort(a+1,a+1+n);
memset(f,0x3f,sizeof(f));
for(int i=0;i<=32;++i) f[0][i]=0;
for(int i=1;i<=k;++i) f[i][0]=i;
for(int i=1;i<=n;++i){
int x=upper_bound(a+1,a+1+n,a[i]/2)-a;
b[i]=x-1;
}
for(int i=1;i<=n;++i)
for(int j=1;j<=32;++j)
f[i][j]=min(f[i-1][j]+1,f[b[i]][j-1]);
for(int i=0;i<=32;++i)
if(f[n][i]<=k) return printf("%d %d\n",i,f[n][i]),0;
return 0;
}
D 树的颜色 :
题面
我们有一棵有n个节点的树(节点编号 \(1\sim n\)),每条边要么是白色,要么是黑色,一开始所有的边都是白色,需要支持三种操作:
1 u v:将 \(u-v\) 路径上所有的边的颜色改变,即黑变白,白变黑;
2 u v:将 \(u-v\) 路径上所有相邻的边的颜色改变,相邻的边表示仅有一个端点在该路径上的边;
3 u v:求出 \(u-v\) 路径上黑色边的数量。
对于 \(100\%\) 的数据,\(1\le n,q\le 100000\)。
输入样例
10
5 9
7 5
6 5
5 8
10 5
3 5
2 9
7 4
6 1
10
2 10 5
1 4 9
3 1 1
3 7 8
3 9 10
1 7 9
3 4 8
1 4 1
2 10 2
2 1 1
输出样例
0
1
0
3