这个题其实和之前 \(NFLS\) 一道题很像,但是还是没做出来,因为当时漏了一个点没注意到,这次赛时就暴毙了。
首先很显然的是拆贡献,寻找每个连通块构成的可能贡献。
期望不好算,我们转成概率乘价值,再转成 \(\frac {\text{方案数}}{\text{总方案数}}\times value\)
我们记 \(sr_S,sb_S\) 表示 \(S\) 集合中红色有多少个,以及蓝色有多少个。
如果一个连通块内部要保证能自己构成一个连通块,那么要满足 \(sr_S=sb_S\)
那么我们的答案就是 \(ans=\sum\limits_{i} \frac {f_i\times (m-sr_i)!}{m!}\)
然后我们现在要求一个连通块中连边(保证是恰好一个),这个东西经典 \(trick\) ,考虑容斥。
\(f_i=f_i-\sum\limits_{j\in i} f_j\times (sr_i-sr_j)!\)
\(\color{red}\text敲黑板\) ,我们这里容斥有一个注意事项,就是说我们一定要钦定一个点在 \(j\) 中,不然我们就会减重。
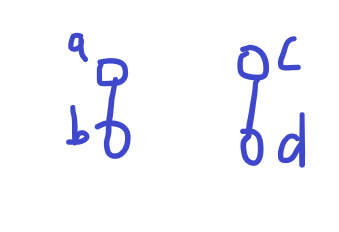
假如 \(a,b,c,d\) 都属于 \(i\) 这个集合。
然后我们枚举 \(j=(a,b),j=(c,d)\) 时就会减重,就是说当你枚举了一个集合,然后你枚举的另一个集合也合法的时候,那么就会减掉重复的,就错了。
而当我们钦定了一个点后,我们的补集就算也是合法的,这样我们也只会计算一次,同时可以保证对于任何都可以计算到,不重不漏。
时间复杂度 \(O(3^n)\)
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int N=(1<<17)+10,M=1e5+10,MODD=998244353;
int n,m;
int sr[N],sb[N],R[20],B[20];
LL pw[M],inv[M],f[N];
int main () {
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i) {
int x;
scanf("%d",&x);
++R[x];
}
for(int i=1;i<=m;++i) {
int x;
scanf("%d",&x);
++B[x];
}
pw[0]=inv[0]=inv[1]=1;
for(int i=1;i<=m;++i)
pw[i]=pw[i-1]*i%MODD;
for(int i=2;i<=m;++i)
inv[i]=(MODD-MODD/i)*inv[MODD%i]%MODD;
for(int i=2;i<=m;++i) (inv[i]*=inv[i-1])%=MODD;
LL S=(1<<n)-1;
for(int i=1;i<=S;++i) {
for(int j=1;j<=n;++j) {
if(!(i&(1<<(j-1)))) continue;
sr[i]+=R[j];
sb[i]+=B[j];
}
}
LL ans=0;
for(int i=1;i<=S;++i) {
if(sr[i]!=sb[i]) continue;
f[i]=pw[sr[i]];
int p=(i&(-i));
for(int j=i;j;j=(j-1&i)) {
int t=(i^j);
if(!(j&p)||j==i) continue;
f[i]=(f[i]-f[j]*pw[sr[t]]%MODD+MODD)%MODD;
}
(ans+=f[i]*pw[m-sr[i]]%MODD*inv[m]%MODD)%=MODD;
}
printf("%lld\n",ans);
return 0;
}