2023年12月28日
XOR Tree
\(\mathtt{TAGS}\):树上启发式合并 + 异或 + 贪心
\(\mathtt{ESTIMATION}\):非常好的启发式合并题目
First.如何去除 \(0\) 路径
对于一条路径 \(u \to v\),要使其不为 \(0\) 肯定是将 \(\mathtt{LCA} (u,v)\) 变为 \(2 ^ {30 + x}\) 最好,这样异或值的第 \(30 + x\) 位一定为 \(1\)(因为 \(a_i \le 2 ^ {30}\)),修改之后,\(u,v\) 在 \(\mathtt{LCA} (u,v)\) 为根的子树内的路径都一定不为 \(0\) 了。显然,这样是最优的。
Second.如何快速判断一颗子树下有无 \(0\) 路径
首先,对于 \(u \to v\) 的路径权值 \(dis_{u, v}\) 可以化为 \(dis_{u, 1} \oplus dis_{v, 1} \oplus a_{\mathtt{lca}(u,v)}\)。
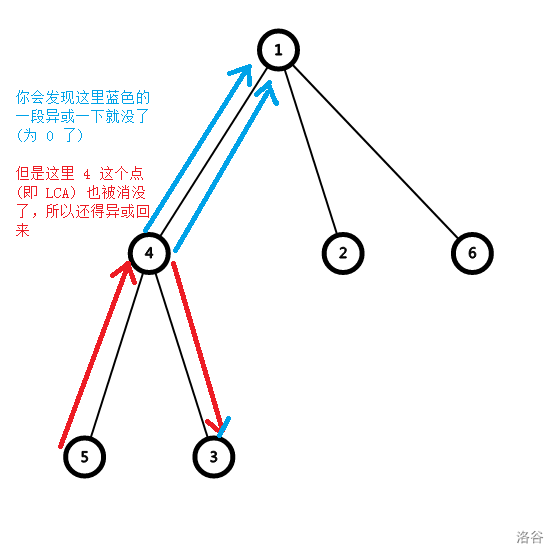
其实知道这个就可以去做 P4551 了。
这个时候可以用一个 set 储存该子树所有 \(dis_{u, 1}\) 的值。然后枚举一个 \(v\) 查找有无 \(dis_{v, 1} \oplus a_u\) 在其中,如果有,那么他们异或起来为 \(0\),就是有 \(0\) 路径。
然后就是把这个子树删除,set 合并到它的父亲上。
这样,大体思路就出来了,暴力的话时间复杂度 \(\text{O}(n ^ 2 \log n)\)(枚举节点的 \(n ^ 2\) 和 set 的 \(\log n\))。
Third.优化时间复杂度
启发式合并,每次将大小小一些的集合合并到大一些的集合上,执行 \(\log n\) 次,节点数就会达到 \(n\)。所以只会合并 \(\log n\) 次。
总时间复杂度为 \(\text{O}(n \log^2 n)\).
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n;
vector<int> G[N];
int a[N], dis[N];
void dfs(int u, int fa) {
dis[u] = a[u];
if(fa) dis[u] ^= dis[fa];
for (auto v : G[u]) {
if(v != fa) dfs(v, u);
}
}
set<int> s[N]; // 快速查找有无 0 路径
void move (int u, int v) { // 合并
for (auto x : s[u]) s[v].insert(x);
s[u].clear();
}
int ans = 0;
void dfs2(int u, int fa) {
bool mark = 0;
s[u].insert(dis[u]);
for (auto v : G[u]) {
if(v != fa) {
dfs2(v, u);
if(s[u].size() < s[v].size()) swap(s[u], s[v]); // 保证是小的合并至大的里面【启发式合并】
for (auto x : s[v]) mark |= s[u].count(x ^ a[u]); // 如果存在 dis[u] = x ^ a[u] 说明子树中存在异或路径为 0 的路径
move(v, u);
}
}
if(mark) ans ++, s[u].clear(); // 如果存在,那么该节点需要删除
}
signed main() {
ios::sync_with_stdio(0);
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i < n; i ++) {
int u, v;
cin >> u >> v, G[u].push_back(v), G[v].push_back(u);
}
dfs(1, 0);
dfs2(1, 0);
cout << ans << endl;
return 0;
}
2023年12月31日
P5304旅行者
\(\mathtt{TAGS}\): 多源多汇最短路,二进制分组
\(\mathtt{ESTIMATION}\):非常新奇的套路,让我的大脑震碎
题意简述
给定 \(k\) 个点和一张有向图,求以这 \(k\) 个点为起点和终点的最短路中最短的一条的长度。
First. 怎么求多源多汇最短路
solution.1
超级源点和超级汇点,超级源点以 \(0\) 的权值连接所有起点,所有终点以 \(0\) 的权值连向超级汇点,从超级源点出发,到超级汇点,即为多源多汇的最短路的长度。
solution.2
对于 dijkstra 算法,直接把所有源点初始放进 \(s\) 集合里,\(dis\) 设为 \(0\),正常跑一遍即可。
But,这道题的起点和终点是不固定的!
所以第一种做法先暂不考虑。
Second. 怎么分起点终点
*MikeZ = & shuffle
直接 shuffle,随机分组!
-- by MikeZ
很不幸的是,这题没有很多时间让你反复跑随机化来获得正确答案,正确率不高。
二进制分组
对于每个标记的节点 \(u\),考虑它的二进制表示法,按照每一位二进制为 \(0\) 或是 \(1\) 来确定它是哪个集合的。而且由于二进制某一位不同的数一定就不相等,所以不会出现起点 = 终点的情况。
Code
const int N = 2e5 + 10;
int n, m, k;
vector< pi > G[N];
ll dis[N];
bool vis[N];
int li[N];
ll dijkstra (int pos, int val) { // pos 表示 二进制的第几位,val表示是1为S集还是 0 为 S 集
priority_queue<pi, vector<pi>, greater<pi> > q;
memset(dis, 0x3f, sizeof dis);
memset(vis, 0, sizeof vis);
for (int i = 1; i <= k; i ++) {
int x = li[i];
if(((x >> (pos - 1)) & 1) == val) {
dis[x] = 0;
q.push({0, x});
}
}
while(!q.empty()) {
int u = q.top().second;
q.pop();
if(vis[u]) continue;
vis[u] = 1;
for (auto e : G[u]) {
int v = e.first, w = e.second;
if(dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
q.push({dis[v], v});
}
}
}
ll minn = 0x3f3f3f3f3f3f3f3f;
for (int i = 1; i <= k; i ++) {
int x = li[i];
if(((x >> (pos - 1)) & 1) != val) {
minn = min(dis[x], minn);
}
}
return minn;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int t;
cin >> t;
while(t --) {
cin >> n >> m;
for (int i = 1; i <= n; i ++) G[i].clear();
for (int i = 1; i <= m; i ++) {
int u, v, w;
cin >> u >> v >> w;
G[u].push_back({v, w});
}
cin >> k;
for (int i = 1; i <= k; i ++) cin >> li[i];
ll ans = 0x3f3f3f3f3f3f3f3f;
for (int i = 0; i < 24; i ++) { // 枚举二进制位数
ans = min(ans, dijkstra(i, 0));
ans = min(ans, dijkstra(i, 1));
}
if(ans == 0x3f3f3f3f3f3f3f3f) cout << -1 << '\n';
else cout << ans << '\n';
}
return 0;
}
QTREE2 - Query on a tree II
\(\mathtt {TAGS}\):\(\mathtt{LCA}\),倍增,树上操作
\(\mathtt {APPRAISE}\):倍增板题。
前置知识
定义
由于根节点是哪一个对本题的求解并没有影响(因为树上两点的简单路径是唯一的),所以本文中默认根节点为 \(1\)。
- \(dis_{u,v}\) 指 \(u\) 到 \(v\) 的唯一简单路径长度。
- \(d_{u}\) 指 \(u\) 到根节点的路径长度。
- \(fa_{u, k}\) 指 \(u\) 的第 \(2 ^ k\) 个祖先。
- \(dep_u\) 指 \(u\) 的深度。
First. 求 \(dis_{u, v}\)
方法 1:
因为 \(u,v\) 不一定在同一颗子树上,直接求 \(dis_{u, v}\) 不好求,那么我们尝试将其转化为我们好求的值 \(d_u\) 和 \(d_v\),通过他们得到 \(dis_{u,v}\)。
不妨把 \(dis_{u, v}\) 拆解成 \(dis_{u, lca(u,v)}\) 和 \(dis_{\text{lca(u,v)},v}\),此时由于 \(\text{lca(u,v)}\) 是 \(u\) 的祖先,所以它一定在 \(u\) 到 根节点的路径上,那么 \(dis_u = d_u - d_{\text{lca(u,v)}}\),同理,\(dis_v = d_v - \text{lca(u,v)}\)。
所以 \(dis_{u,v}\) 就化为了 \(d_u + d_v - d_{\text{lca(u,v)}} \times 2\)。
如下图:
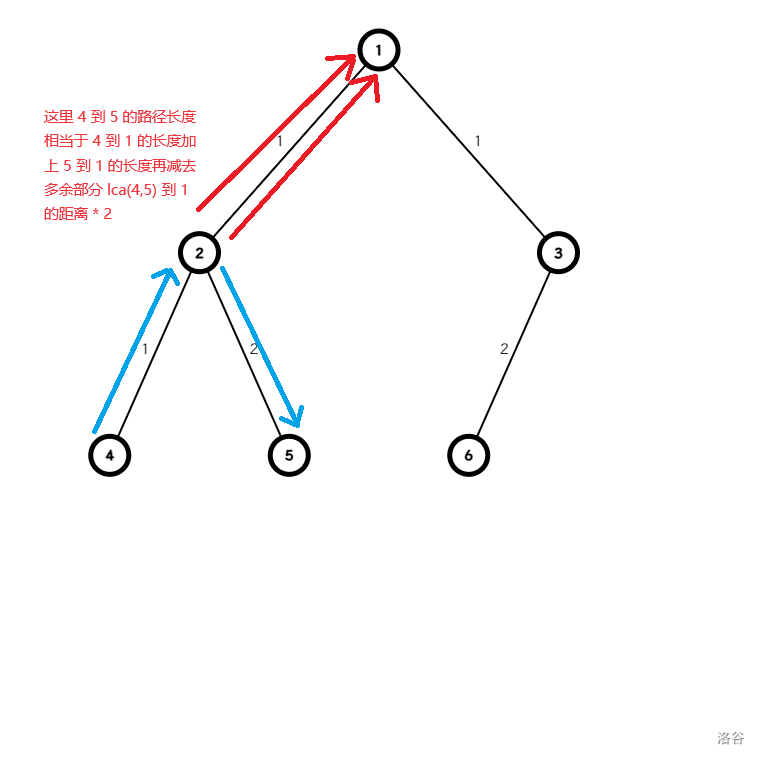
方法 2.
使用倍增在 \(\mathtt{LCA}\) 的过程中求出 \(dis_{u,\text{lca(u,v)}}\) 和 \(dis_{v, \text{lca(u,v)}}\)。
定义 \(ds_{u,k}\) 为 \(u\) 到其第 \(2 ^ k\) 个祖先的简单路径距离(可以预处理)。
在用倍增向上跳时,将两个点跳的距离加在一个 \(tmp\) 上,最后跳至 \(\mathtt{LCA}\) 后,\(tmp\) 即为所求。
这里作者使用的方便一点的方法 1。
方法 2 在此给出代码:
- len 即上文中的 \(ds\)。
void dfs(int u, int f) {
dep[u] = dep[f] + 1, fa[u][0] = f, len[u][0] = e[u][f];
for (int i = 1; ; i ++) {
fa[u][i] = fa[fa[u][i - 1]][i - 1];
len[u][i] = len[fa[u][i - 1]][i - 1] + len[u][i - 1]; // 预处理
if (fa[u][i] == 0) {
k = max(k, i - 1);
break;
}
}
for (auto v : g[u]){
if(v != f){
dfs(v, u);
}
}
}
int lca(int u, int v){
if(dep[u] < dep[v]) swap(u, v);
int x = u, y = v;
int lu = 0, lv = 0; // 统计两边跳的距离
for (int i = k; i >= 0; i --){
if(dep[fa[u][i]] >= dep[v]) lu += len[u][i], u = fa[u][i];
}
if(u == v) return lu + lv;
for (int i = k; i >= 0; i --){
if(fa[u][i] != fa[v][i]) lu += len[u][i], u = fa[u][i], lv += len[v][i], v = fa[v][i];
}
lu += len[u][0], lv += len[v][0];
return lu + lv;
}
Second. 求 \(u\) 到 \(v\) 路径上的第 \(k\) 个点
这个点的位置有两种情况:
- 在 \(u\) 到 \(\mathtt{LCA}\) 的路径上。
- 在 \(\mathtt{LCA}\) 到 \(v\) 的路径上。
对于情况 1:
相当于求 \(u\) 的第 \(k - 1\) 个祖先(因为 \(u\) 为第一个点)
对于情况 2:
转化一下,相当于求 \(v\) 的第 \(\text{路径点数 - k}\) 个祖先。
如下图蓝色路径:
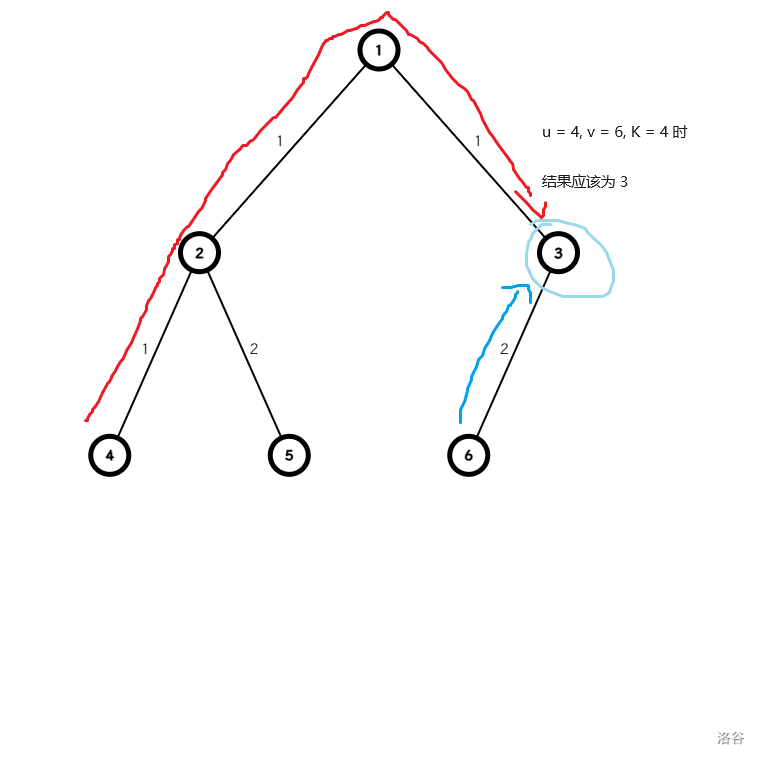
接着直接将 \(k\) 二进制拆分,然后用 \(f_u\) 向上跳至第 \(k\) 祖先即可(具体实现详见代码)。
时间复杂度
- 倍增预处理:\(\text{O}(n \log {n})\)
- \(\mathtt{LCA}\):\(\text{O}(\log n)\)
总时间复杂度:$\text{O}(t \times (n \log {n}+ q \log n)) $
可以通过此题。
Code
vector< pair <int , int> > G[N];
int f[N][30];
ll dis[N];
int dep[N] , K;
void dfs(int u , int fa) { // 预处理
dep[u] = dep[fa] + 1;
f[u][0] = fa;
for (int i = 1; ; i++) {
f[u][i] = f[f[u][i - 1]][i - 1];
if (f[u][i] == 0) {
K = max(K , i - 1);
break;
}
}
for (auto e : G[u]) {
int v = e.first , w = e.second;
if (v != fa) {
dis[v] = dis[u] + w;
dfs(v , u);
}
}
}
int lca(int u , int v) { // 倍增求 LCA
if (dep[u] < dep[v]) swap(u , v);
for (int i = K; i >= 0; i--) {
if (dep[f[u][i]] >= dep[v]) u = f[u][i];
}
if (u == v) return u;
for (int i = K; i >= 0; i--) {
if (f[u][i] != f[v][i]) u = f[u][i] , v = f[v][i];
}
return f[u][0];
}
int kth_num(int u , int v , int k) {
int Lca = lca(u , v);
int dul = dep[u] - dep[Lca] + 1;
if (dep[u] - dep[Lca] + 1 >= k) { // 情况 1
int tmp = u;
k--; // k - 1 个祖先
for (int i = log2(k); i >= 0; i--) { // 二进制拆分
if ((k >> i) & 1) { // 需要跳 2^K 次
tmp = f[tmp][i];
}
}
return tmp;
} else {// 情况 2
k -= dep[u] - dep[Lca] + 1;
k = dep[v] - dep[Lca] - k;
int tmp = v;
for (int i = log2(k); i >= 0; i--) {// 二进制拆分
if ((k >> i) & 1) {// 需要跳 2^K 次
tmp = f[tmp][i];
}
}
return tmp;
}
}
signed main() {
ios::sync_with_stdio(0);
int t;
cin >> t;
while (t--) {
cin >> n;
for (int i = 1; i < n; i++) {
int u , v , w;
cin >> u >> v >> w;
G[u].push_back({ v, w });
G[v].push_back({ u, w });
}
dfs(1 , 0);
string opt;
int u , v , k;
while (cin >> opt) {
if (opt == "DONE") break;
if (opt == "DIST") {
cin >> u >> v;
int Lca = lca(u , v);
cout << dis[u] + dis[v] - dis[Lca] * 2 << endl;
} else {
cin >> u >> v >> k;
cout << kth_num(u , v , k) << endl;
}
}
// 多测一定要清空!!!!!!
// 本人在此 RE + WA 了三次
for (int i = 1; i <= n; i++) G[i].clear();
memset(f , 0 , sizeof f);
memset(dis , 0 , sizeof dis);
memset(dep , 0 , sizeof dep);
}
return 0;
}