其实 2022 年省选前联考出过类似的套路,但当时太鸽了就没有总结。
阶梯网格计数问题是指以下一类问题:
问题:给定一个 \(n\) 列阶梯状网格图,第 \(i\) 列高度为 \(c_i\)(保证 \(c_i\) 不降),每次可以向上或向右走一步,不能超出网格边界(即所有经过的点 \((x,y)\) 必须满足 \(0\le x\le n,0\le y\le c_x\),问从左下到右上有多少种方案。对 \(998244353\) 取模。
\(n\le 10^5\)
首先 \(n^2\) 的 DP 很 trivial。但是似乎没有优化的前途,因此我们只能放弃这个想法。
考虑最特殊的情况:如果没有 \(c_i\) 的限制(即每一列高度相等),那么方案数容易使用组合数计算。因此我们尝试将原问题向不受 \(c_i\) 限制的情况靠拢。一个非常 naive 的想法是直接对原网格图分治 NTT,即处理一个区间 \([l,r]\) 时求出左边界上每个点走到右边界的方案数,但是你会发现不论怎么样都绕不开 \(c_i\) 的限制,原因是在每一列你可以向上走任意多格,这意味着哪怕你在 \(l\) 这一列时在最下面,走到 \(r\) 的时候都有可能因突破 \(c_i\) 的限制而不合法。
那么究竟应该怎么处理呢?我们先做一个转化:在原网格中,考虑左上到右下的那条对角线,我们分别计算出左下角和右上角到对角线上每个点的方案数,然后枚举中间点计算方案数累加即可。显然左下和右上两部分的计算是对称的,因此只用考虑一边,不妨考虑左下角。
为什么要做这个转化呢?假设有如下图所示的网格图,其中阴影部分表示对角线以下的部分:

那么我们考虑将第 \(i\) 行上每个点向右整体平移 \(i\) 格,容易发现原来竖直向上的线变成了斜向上 \(45\) 度的线,原本的网格图进而变成如下的模样:
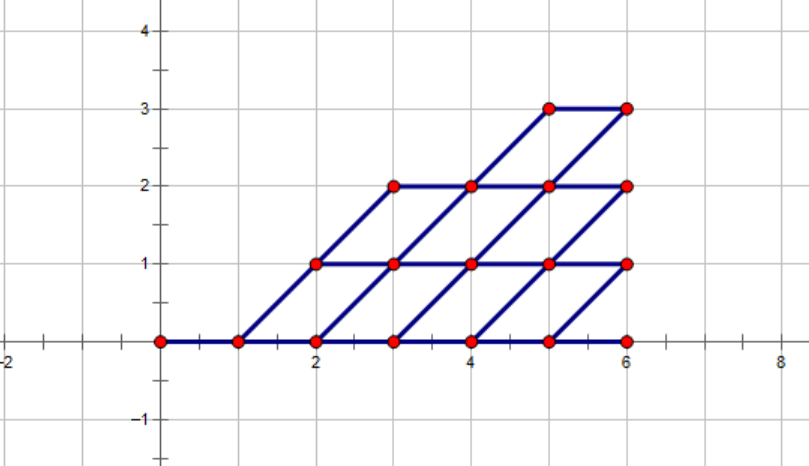
换句话说,在上面那幅图中,从 \((0,0)\) 开始,每次可以向右或向上走到对角线上每个点的方案数,就等价于在下面那幅图中,从 \((0,0)\) 开始,每次可以向右或向右上走一步,走到最右侧一列上每个点的方案数。
于是问题可以转化为:有一张网格图,第 \(i\) 列有限制 \(c'_i\)(其中 \(c'_i\) 可以由 \(c_i\) 做简单变换得到),每次可以向上或向右上走一步,且经过的所有点 \((x,y)\) 必须满足 \(y\le c'_x\),求走到右侧一列上每个点的方案数。更进一步,容易发现变换得到的 \(c'_i-c'_{i-1}\le 1\),即相邻两列的差 \(\le 1\)。
那么问题就来了,这样变换有什么好处呢?还是延续上文中的分治 NTT 做法,假设我们要计算 \(dp_{l,*}\) 到 \(dp_{r,*}\) 的贡献,那么我们发现,对于 \(j<c'_r-(r-l)\),\(dp_{l,j}\) 对 \(dp_{r,*}\) 的贡献不用考虑 \(c'\) 的限制!这是因为每次横坐标增加 \(1\),纵坐标至多增加 \(1\),因此下面的部分必然不会越过网格的高度限制,换句话说,对于下图中标注的区域,它们的贡献可以直接一遍卷积求得!

这样大致思路出来了,考虑具体怎么实现,方便起见,设 \(lim=c'_r-(r-l)\),那么考虑分治区间 \([l,r]\) 时候,我们往参数里另外传一个长度为 \(c'_l-lim+1\) 的数组 \(F\),表示 \(dp_{l,lim},dp_{l,lim+1},dp_{l,lim+2},\cdots,dp_{l,c'_l}\) 的值,然后返回一个长度为 \(c'_r-lim+1\) 的数组,表示只考虑 \(dp_{l,lim},dp_{l,lim+1},dp_{l,lim+2},\cdots,dp_{l,c'_l}\) 对 \(dp_r\) 的贡献的情况下,\(dp_{r,lim},dp_{r,lim+1},\cdots,dp_{r,c'_r}\) 的值分别是多少。考虑怎么进一步划分为更小的子问题,从中间将网络劈开,记 \(mid=\lfloor\dfrac{l+r}{2}\rfloor\),那么我们将整个部分分为 \(dp_l\to dp_{mid}\) 和 \(dp_{mid}\to dp_r\),两部分是完全相同的,以左半边为例,记 \(lim'=c'_{mid}-(mid-l)\),那么我们先求出 \(lim'\) 以上的部分对 \(dp_{mid}\) 的贡献(即蓝色的分形),这部分就进一步递归,而 \(lim'\) 以下 \(lim\) 以上的部分直接卷积即可(即橙色的分形),两部分加起来就得到 \(dp_l\to dp_{mid}\) 的贡献,然后再分治右半边也能得到 \(dp_r\)。
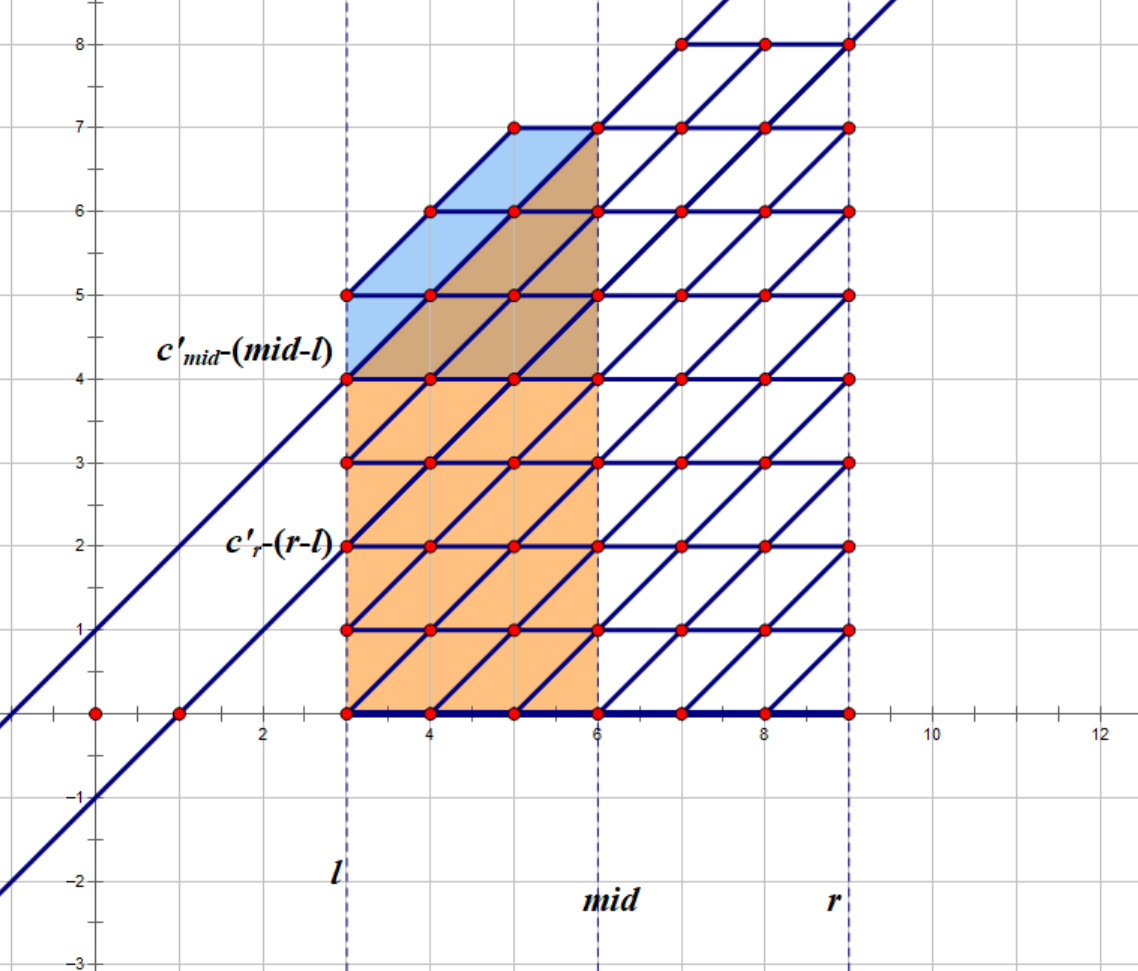
容易发现传入的多项式、返回的多项式、进行卷积的多项式的长度都与区间长度同阶。因此总复杂度 \(n\log^2n\)。我们就完美地解决了这个问题。
回到 CF 这个题上来。将左括号视作 \(+1\),右括号视作 \(-1\),求出前缀和 \(sum_i\)。找到前缀和最小的位置 \(sum_p\),容易证明 \(k=sum_n-2sum_p\),具体策略是 \(p\) 及左边的部分只删右括号,\(p+1\) 及右边的部分只删左括号。以左边为例,RBS 的限制等价于,前 \(i\) 个右括号中至少删 \(lim_i\) 个,并且最终必须恰好删除 \(lim_c\) 个(其中 \(c\) 为左边右括号的个数),其中 \(lim\) 简单地扫一遍就可以求得。将删第 \(i\) 个左括号视作第 \(i\) 步向右走,不删视作第 \(i\) 步向右上走,那么问题转化为上述模型。直接套用上述做法即可。
const int MAXN=5e5;
const int MAXP=1<<20;
const int MOD=998244353;
const int pr=3;
const int ipr=332748118;
int fac[MAXN+5],ifac[MAXN+5];
void init_fac(int n){
for(int i=(fac[0]=ifac[0]=ifac[1]=1)+1;i<=n;i++)
ifac[i]=1ll*ifac[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=1;i<=n;i++){
fac[i]=1ll*fac[i-1]*i%MOD;
ifac[i]=1ll*ifac[i-1]*ifac[i]%MOD;
}
}
int binom(int n,int k){return 1ll*fac[n]*ifac[k]%MOD*ifac[n-k]%MOD;}
int qpow(int x,int e){
int ret=1;
for(;e;e>>=1,x=1ll*x*x%MOD)if(e&1)ret=1ll*ret*x%MOD;
return ret;
}
int rev[MAXP+5];
void NTT(vector<int>&a,int len,int type){
int lg=31-__builtin_clz(len);
for(int i=0;i<len;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<lg-1);
for(int i=0;i<len;i++)if(rev[i]<i)swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=qpow((type<0)?ipr:pr,(MOD-1)/i);
for(int j=0;j<len;j+=i){
for(int k=0,w=1;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*w*a[(i>>1)+j+k]%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type<0){
int iv=qpow(len,MOD-2);
for(int i=0;i<len;i++)a[i]=1ll*a[i]*iv%MOD;
}
}
vector<int>conv(vector<int>a,vector<int>b){
int LEN=1;while(LEN<a.size()+b.size())LEN<<=1;
a.resize(LEN,0);b.resize(LEN,0);NTT(a,LEN,1);NTT(b,LEN,1);
for(int i=0;i<LEN;i++)a[i]=1ll*a[i]*b[i]%MOD;
NTT(a,LEN,-1);return a;
}
char s[MAXN+5];int n,sum[MAXN+5];pii mn=mp(0,0);
int lim[MAXN+5],len,res;
vector<int>solve(int l,int r,vector<int>F){
int pos=max(lim[r]-(r-l),0);
if(r-l==1){
vector<int>res(lim[r]-pos+1);
for(int i=0;i<F.size();i++)for(int j=i;j<res.size();j++)
res[j]=(res[j]+F[i])%MOD;
return res;
}
int mid=l+r>>1,pos_mid=max(lim[r]-(r-mid),0),pos_l=max(lim[mid]-(mid-l),0);
vector<int>nF,G(lim[mid]-pos+1),H(lim[r]-pos+1),G1,G2,H1,H2,A,B;
for(int i=pos_l;i<=lim[l];i++)nF.pb(F[i-pos]);
G1=solve(l,mid,nF);
for(int i=pos_l;i<=lim[mid];i++)G[i-pos]=(G[i-pos]+G1[i-pos_l])%MOD;
if(pos_l!=pos){
A.clear();B.clear();
for(int i=pos;i<pos_l;i++)A.pb(F[i-pos]);
for(int i=0;i<=mid-l;i++)B.pb(binom(mid-l,i));
G2=conv(A,B);
for(int i=0;i<min(G.size(),G2.size());i++)G[i]=(G[i]+G2[i])%MOD;
}
nF.clear();
for(int i=pos_mid;i<=lim[mid];i++)nF.pb(G[i-pos]);
H1=solve(mid,r,nF);
for(int i=pos_mid;i<=lim[r];i++)H[i-pos]=(H[i-pos]+H1[i-pos_mid])%MOD;
if(pos!=pos_mid){
A.clear();B.clear();
for(int i=pos;i<pos_mid;i++)A.pb(G[i-pos]);
for(int i=0;i<=r-mid;i++)B.pb(binom(r-mid,i));
H2=conv(A,B);
for(int i=0;i<min(H.size(),H2.size());i++)H[i]=(H[i]+H2[i])%MOD;
}
// printf("solve %d %d %d <",l,r,pos_mid);
// for(int i=0;i<F.size();i++)printf("%d%c",F[i],",>"[i+1==F.size()]);
// printf("\n");
// for(int x:G)printf("%d ",x);printf("\n");
// for(int x:H)printf("%d ",x);printf("\n");
return H;
}
int calc(){
if(!len)return 1;
for(int i=1;i<=len;i++)lim[i]=i-lim[i];
// for(int i=1;i<=len;i++)printf("%d%c",lim[i]," \n"[i==len]);
vector<int>vec=solve(0,len,vector<int>{1});
return vec.back();
}
int main(){
scanf("%s",s+1);n=strlen(s+1);init_fac(MAXN);
for(int i=1;i<=n;i++)sum[i]=sum[i-1]+((s[i]=='(')?1:-1);
for(int i=1;i<=n;i++)chkmin(mn,mp(sum[i],i));
memset(lim,0,sizeof(lim));int cur=0,cmn=0;
for(int i=1;i<=mn.se;i++){
if(s[i]=='(')cur++;
else{
cur--;chkmin(cmn,cur);
lim[++len]=-cmn;
}
}
res=calc();
memset(lim,0,sizeof(lim));len=cur=cmn=0;
for(int i=n;i>mn.se;i--){
if(s[i]==')')cur++;
else{
cur--;chkmin(cmn,cur);
lim[++len]=-cmn;
}
}
res=1ll*res*calc()%MOD;
printf("%d\n",res);
return 0;
}
/*
())())
())())))((())))))
*/