CF1229F Mateusz and Escape Room
很好的题目。
对于此类在环上的问题,一个经典的思路是断环成链。我们先形式化的描述题意,即给 \(i\) 向 \(i + 1\) 定一个流量 \(x_i\)(可能为负)。限制则为
先定下 \(x_0 = c\),则问题转化到序列上。
考虑最最朴素的暴力,设 \(f_{i,j}\) 表示考虑到 \(x_i = j\) 的最小代价,最终答案为 \(f_{n,c}\)。转移为
考虑这个 dp 的性质,经过简单的模拟可以发现这个 \(f_i\) 是一个关于 \(k\) 的分段函数,其中每一段都是一次函数且斜率递增。这启发我们利用记录分段函数每一段的信息的方法来维护这个函数。至于证明在下面的具体做法可以归纳得到。
初始时只有 \(f_{0,c} = 0\),我们考察每次移动 \(i\) 对函数造成的影响。
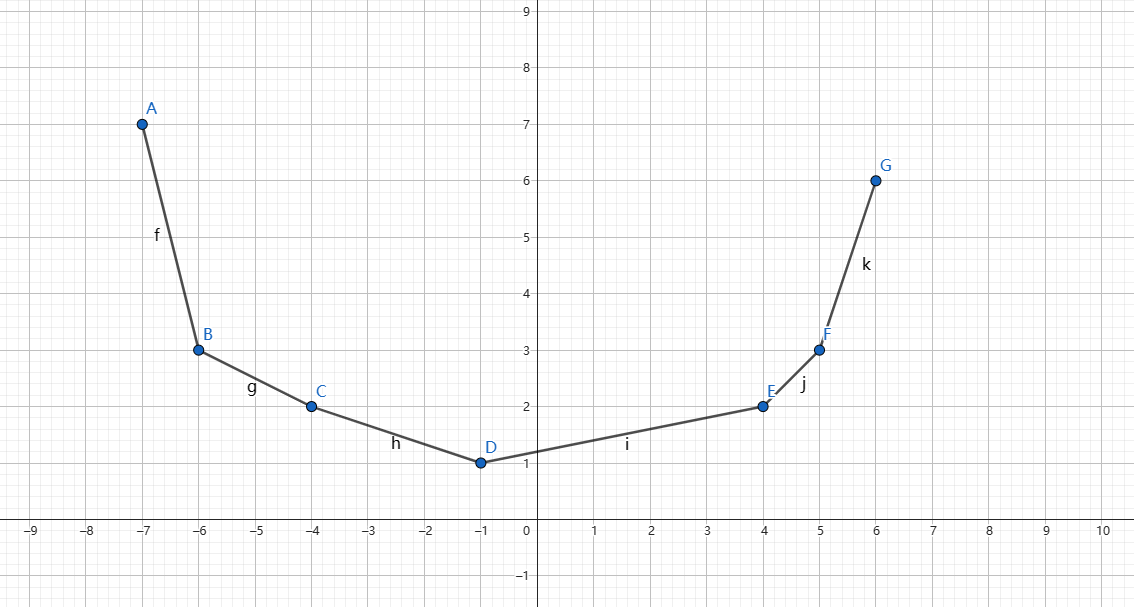
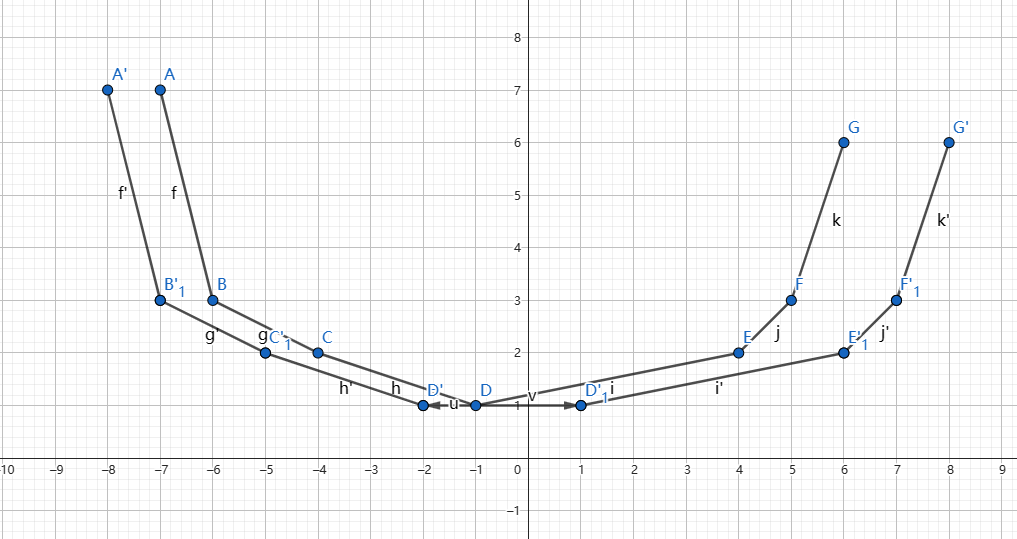
如图,假设此为 \(f_{i - 1}\) 的图像(不要在意纵坐标的值),则通过对上面条件的转化得到 \(f_{i - 1, j}\) 贡献到 \(f_{i, k}\) 当且仅当 \(j \in [l_i - a_i + k, r_i - a_i + k]\)。我们先不考虑 \(+|k|\) 部分的贡献,那么结果的图像如图
即最低点左侧向左平移 \(r_i - a_i\),右侧向右平移 \(a_i - l_i\)。
现在再来加上 \(|k|\) 的贡献,不难发现只会将 \(x = 0\) 左侧线段斜率 \(-1\),右侧线段斜率 \(+1\)。故斜率递增的性质始终不变。
现在来考虑如何维护这个凸包,由于每次斜率只会改变 \(1\),我们直接记录在哪些点发生了斜率的改变即可,我们需要支持加入一个单点和全局平移,全局平移的部分可以直接记一个平移量完成,而加入单点可以通过堆来完成。注意最低点左侧和右侧分别需要维护一个大根堆和一个小根堆。当然,还需要维护最低点的纵坐标。查询时顺着凸包来算答案即可。
这样在确定了 \(x_0\) 的前提下就可以在 \(O(n \log n)\) 的时间内求出答案了。
但是我们还需要枚举 \(x_0\) 呀!考虑减少枚举量,设 $F(x) $表示 \(x_0 = x\) 时的答案,打表发现 \(F(x)\) 是一个下凸包,因此三分即可,复杂度 \(O(n \log n \log \sum a)\)。
下面证明这个结论,直接上定义,只需证 \(\frac{F(p) + F(q)}{2} \ge F(\frac{p+q}{2})\)。我们先把定义域扩充到实数,答案不变,这是因为题意正是一个上下界费用流的模拟,因此实数规划和整数规划是等同的。
接下来,我们假定有两组合法方案 \((p_0,p_1...p_{n-1}), (q_0,q_1...q_{n-1})\),不难发现 \((r_0,r_1...r_{n-1}) = (\frac{p_0 + q_0}{2},\frac{p_1+q_1}{2}...\frac{p_{n-1}+q_{n-1}}2)\) 依然合法,而 \(|\frac{p + q}{2}| \le \frac{|p| + |q|}{2}\),对上述每一项都运用这一不等式即可得证!
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
namespace IO {
#define isdigit(x) (x >= '0' && x <= '9')
template<typename T>
inline void read(T &x) {
x = 0; char ch = getchar(); int f = 0;
for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
if(f) x = -x;
}
template<typename T, typename... Rest>
inline void read(T &x, Rest&... rest) {
read(x), read(rest...);
}
template<typename T>
inline void write(T x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) write(x / 10);
putchar(x % 10 + '0');
}
#undef isdigit
}
using namespace IO;
constexpr int N = 2e5 + 10;
int n, a[N], l[N], r[N];
LL _ans = 1e18;
LL solve(LL c) {
priority_queue<LL, vector<LL>, less<LL>> L;
priority_queue<LL, vector<LL>, greater<LL>> R;
for(int i = 1; i <= n; ++i)
L.push(c), R.push(c);
LL Lshift = 0, Rshift = 0, ans = 0;
for(int i = 1; i <= n; ++i) {
Lshift += r[i] - a[i], Rshift += a[i] - l[i];
if(L.top() - Lshift > 0) {
ans += L.top() - Lshift;
R.push(L.top() - Lshift - Rshift);
L.pop(), L.push(Lshift), L.push(Lshift);
}
else if(R.top() + Rshift < 0) {
ans -= R.top() + Rshift;
L.push(R.top() + Rshift + Lshift);
R.pop(), R.push(-Rshift), R.push(-Rshift);
}
else {
L.push(Lshift);
R.push(-Rshift);
}
}
LL tmp = L.top() - Lshift, nxt;
for(LL i = 1; c < tmp; ++i, tmp = nxt)
L.pop(), ans += i * (tmp - max(c, nxt = L.top() - Lshift));
tmp = R.top() + Rshift;
for(LL i = 1; c > tmp; ++i, tmp = nxt)
R.pop(), ans += i * (min(c, nxt = R.top() + Rshift) - tmp);
_ans = min(_ans, ans);
return ans;
}
int main() {
read(n);
LL s = 0;
for(int i = 1; i <= n; ++i)
read(a[i], l[i], r[i]), s += a[i];
for(LL _l = -s, _r = s; _l <= _r; ) {
if(_l == _r) {
solve(_l);
break;
}
LL mid = (_l + _r) / 2;
if(solve(mid) > solve(mid + 1))
_l = mid + 2;
else _r = mid - 1;
}
printf("%lld\n",_ans);
}