1. 上网查找什么是求两个数的最大公约数的欧几里得算法(辗转相除法),提交算法说明和网上链接。
两个整数的最大公约数是能够同时整除它们的最大的正整数。辗转相除法基于如下原理:两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数。 [2
扩展欧几里得算法可用于RSA加密等领域。
假如需要求 1997 和 615 两个正整数的最大公约数,用欧几里得算法,是这样进行的:
1997 ÷ 615 = 3 (余 152)
615 ÷ 152 = 4(余7)
152 ÷ 7 = 21(余5)
7 ÷ 5 = 1 (余2)
5 ÷ 2 = 2 (余1)
2 ÷ 1 = 2 (余0)
至此,最大公约数为1
其计算原理依赖于下面的定理:
gcd(a,b) = gcd(b,a mod b) (不妨设a>b 且r=a mod b ,r不为0)
证法一
a可以表示成a = kb + r(a,b,k,r皆为正整数,且r不为0)
假设d是a,b的一个公约数,记作d|a,d|b,即a和b都可以被d整除。
而r = a - kb,两边同时除以d,r/d=a/d-kb/d,由等式右边可知m=r/d为整数,因此d|r
因此d也是b,a mod b的公约数。
因(a,b)和(b,a mod b)的公约数相等,则其最大公约数也相等,得证。
证法二
假设c = gcd(a,b),则存在m,n,使a = mc, b = nc;
令r = a mod b,即存在k,使r = a-kb = mc - knc = (m-kn)c;
故gcd(b,a mod b) = gcd(b,r) = gcd(nc,(m-kn)c) = gcd(n,m-kn)c;
则c为b与a mod b的公约数;
假设d = gcd(n,m-kn), 则存在x,y, 使n = xd, m-kn = yd; 故m = yd+kn = yd+kxd = (y+kx)d;
故有a = mc = (y+kx)dc, b = nc = xdc; 可得 gcd(a,b) = gcd((y+kx)dc,xdc) = dc;
由于gcd(a,b) = c, 故d = 1;
即gcd(n,m-kn) = 1, 故可得gcd(b,a mod b) = c;
故得证gcd(a,b) = gcd(b,a mod b).
注意:两种方法是有区别的。
2. 参考教材,用伪代码(英语或汉语)实现欧几里得算法(辗转相除法),提交伪代码。
英语:function euclidean_algorithm(a, b):
while b ≠ 0:
remainder = a mod b;
a = b;
b = remainder;
return a;
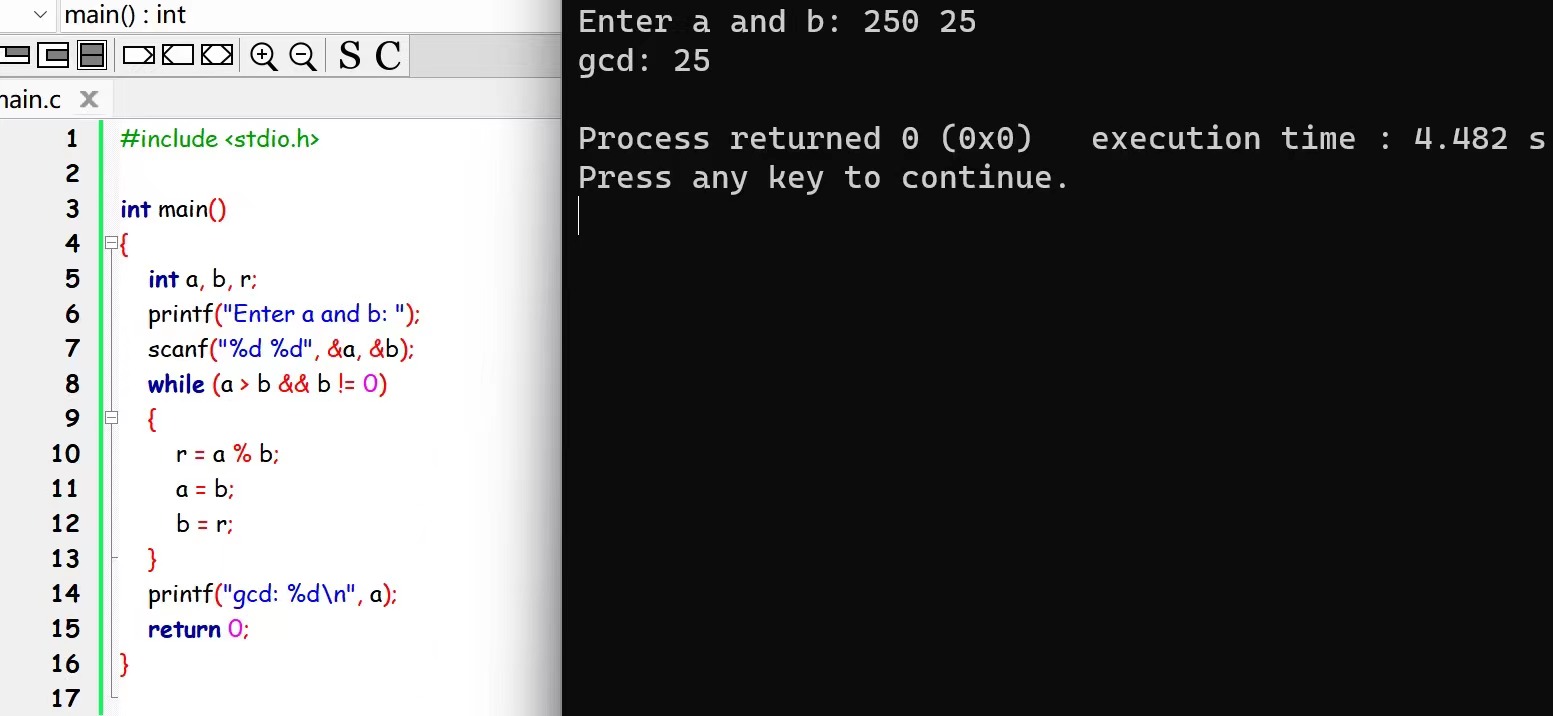
3. 选择几组数据,手动走一下伪代码,测试你写的伪代码是否正确,提交测试过程截图