是 Div2 的 D1 和 D2。
题意
给定一棵 \(n\) 个结点的树,现在有 \(k(k\leq n)\) 个结点上有人。
一个结点是好的当且仅当这个点到所有人的距离之和最小。
求在这 \(n\) 个点中随机取 \(k\) 个点时,好的结点的期望个数,对 \(10^9+7\) 取模。
Easy: \(k\leq 3,n\leq 2*10^5\)
Hard: \(k\leq n\leq 2*10^5\)
Part 1
考虑 Easy 版本。
- \(k=1\) 时,只有一个点是关键点,故答案为 \(1\)。
- \(k=3\) 时,考虑如下三种情况:
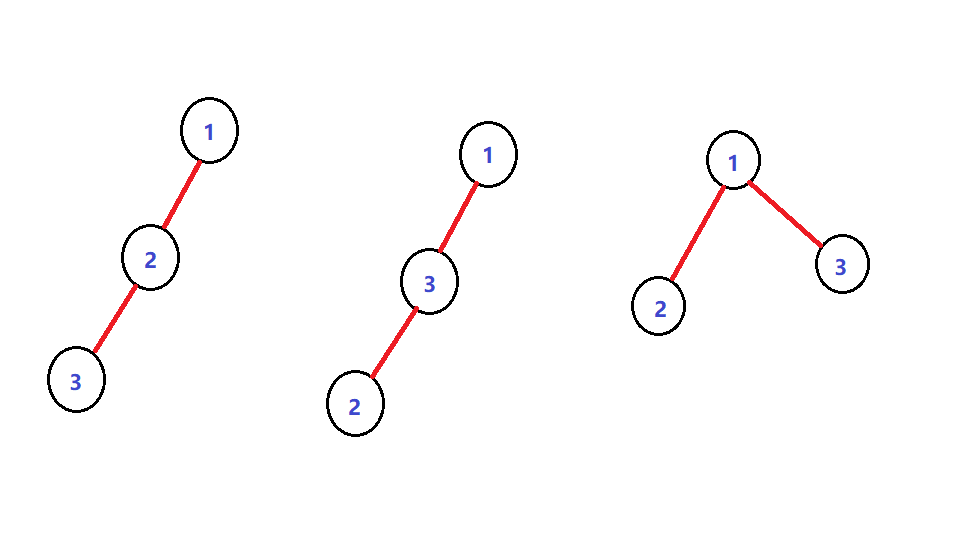
当钦定 \(1\) 与 \(2\) 两个点后,考虑第三个点的位置。
- 当三者在一条链上,且第三个点不在前两个点中间时:显然,中间的点是唯一一个“好点”。
- 第三个点在两者中间时:同上,中间的点是唯一一个“好点”。
- 三者不在一条链上:最上方的点是唯一一个“好点”。
得出结论:\(k=3\) 时答案也为 \(1\)。
- \(k=2\) 时,对于每一条链,中间的每一个点都可以成为“好点”。所以只需要统计各个长度的链共有多少条,简单计数即可。
Part 2
进阶到 Hard 版本。
猜想:当 \(k\) 为奇数时,答案恒为 \(1\)。
证明:设好点为 \(x\),\(k\) 个特殊点组成的序列为 \(a\),则题目可转化成这样一个式子:
当算式 \(abs(x-a_1)+abs(x-a_2)+......+abs(x-a_k)\) 取到最小值时,\(x\) 的取值满足什么条件?
当 \(k\) 为奇数时,\(x\) 即为 \(a_{k/2+1}\)。对应到题目中,\(x\) 仅会有 \(1\) 个取值。故答案恒为 \(1\)。
当 \(k\) 为偶数时呢?显然,\(x\) 的取值应该在 \(a_{k/2}\) 和 \(a_{k/2+1}\) 之间。转化到题目中,则好点 \(x\) 为子树中的一部分有 \(k/2\) 个特殊点,且子树外也有 \(k/2\) 个特殊点的点。直接统计貌似不太好做,将做法转变一下,我们现在只需要统计每一种方案中“好点”的个数大于等于 \(2\) 的期望和。对于每一种方案,其至少存在一个好点。故最后的答案应加上 \(1\)。
Code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define db double
#define mkp make_pair
#define pb push_back
#define P pair<int,int>
#define _ 0
const int N=2e5,mod=1e9+7,MOD=1e9+123,inf=1e18;
int T=1,siz[N+10],ans,fac[N+10],inv[N+10],n,k;
vector<int> e[N+10];
int qpow(int a,int b){
int ans=1;
while(b){
if(b&1) ans=(ans*a)%mod;
b>>=1;
a=(a*a)%mod;
}
return ans;
}
void init(){
fac[0]=1;
for(int i=1;i<=N;i++) fac[i]=fac[i-1]*i%mod;
inv[N]=qpow(fac[N],mod-2);
for(int i=N-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
}
int C(int n,int m){
if(n<m||n<0||m<0) return 0;
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
void dfs(int x,int fa){
siz[x]=1;
for(int y:e[x]){
if(y==fa) continue;
dfs(y,x);
siz[x]+=siz[y];
ans=(ans+C(siz[y],k/2)*C(n-siz[y],k/2))%mod;
}
}
void solve(){
init();
cin>>n>>k;
if(k&1){
cout<<1;
return ;
}
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
e[u].pb(v),e[v].pb(u);
}
ans=C(n,k);
dfs(1,0);
cout<<ans*qpow(C(n,k),mod-2)%mod;
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
// ios::sync_with_stdio(false),cin.tie(0);
while(T--){
solve();
}
return ~~(0^_^0);
}