动态规划的形式理论

动态规划是一类特殊的组合最优化问题的求解方式。

组合最优化问题是在给定有限集合的所有具某些特性的子集簇中，寻找使某种指标达到最优的子集的问题。也即，给定一个基础集合 $P$，在 $P$ 的所有子集（记作 $2^P$，由于可以决定每个元素选或不选）的某个子集 $S \subseteq 2^P$ 上，求拥有最大权值的方案，即 $\operatorname{argmax}_{s \in S} w(s)$。权值由方案中含有的元素所决定，即 $w(s)=f(\{i, i \in s\})$，在很多时候，$f$ 可以拆成每个元素的更为基本的贡献 $g(i)$ 的和、乘积、等等。

例如，在最优上升子序列一题中，基础集合 $P=\{1, 2, \ldots, n\}$ 表示原序列的所有位置，$2^P$ 表示所有子序列，$S$ 为满足 $a_i$ 随 $i$ 上升的所有子序列，$w(s)=|s|$，$g(i)=1$，$w(s)=\sum_{i \in s} g(i)$。

子问题是与原问题相关的部分性的问题，其相关性表现为我们通常用子问题的结果来解决原问题。在组合最优化问题中，子问题通常是在 $P$ 的子集的子集 $2^{P'}$ 中选择拥有相同性质的子集 $S' \subseteq 2^{P'} \subseteq 2^P$，或是直接选择 $S$ 的一个子集 $S' \subseteq S \subseteq 2^P$。

动态规划使用子问题递推的方式解决组合最优化问题。

想要通过将问题拆解为子问题的方式解决组合最优化问题，我们需要其拥有最优子结构性质与无后效性原则。最优子结构指子结构的最优化位置 $\operatorname{argmax}_{s \in S'} w(s)$ 总能推出原结构的最优化位置 $\operatorname{argmax}_{s \in S} w(s)$，而无后效性指的是问题的答案并不依赖于将其划分为子问题的方式。

状态、转移是动态规划的两个组成部分。每个状态表示一个子问题。转移表示子问题之间的数学关系（通常是依赖）。

状态可以被抽象为一个点，而转移可以抽象为一条边。这样，（状态，转移）被抽象为了一张图。这张图是一个 DAG（有向无环图），这是因为子问题的解决具有阶次性，我们总是用阶次更低的解决阶次更高的子问题，很多时候这个阶次是 $|P'|$，有些时候我们无法明述（DAG 不一定是分层图，每条反链都可以自称是一个“层”）。

我们知道，DAG 是可被拓扑排序的。也即存在一个点集的排列顺序使得所有依赖关系 $u \to v$ 满足 $u$ 先比 $v$ 出现。故我们可以按照这个顺序来依次解决子问题。

综上所述，我们对动态规划问题的思考集中在以下几点

如何将具体问题抽象为动态规划模型，进而抽象为 DAG（即使不显式地做）。
DAG 的特殊性质。

也即建模与优化两部分。

对无后效性的举例

一个很简单的例子是整数分拆的朴素递推。我们设 $f_i$ 表示 $i$ 的整数分拆数量，每次在序列后加入一个新的数，则有

\[f_i=\sum_{j < i} f_j \]

这是不对的。因为我们要求的，是分拆的可重集个数。

如 $\{1, 1, 2\}$ 和 $\{1, 2, 1\}$ 和 $\{2, 1, 1\}$ 应为同一种方案，在这里却被计算了多次。

这要求我们对转移进行去重。

集合去重是难的。因为其有后效性，我们需要获得非常多的信息才能判断。

但我们知道，判别两个可重集相同，当且仅当将其排序后序列相同。

我们可以用排序后的序列作为所有在可重集意义下相等的序列的代表元素，故我们只用计算不同的有序序列个数就行。

这便是让子问题的拆分变得无后效性。

后文中我们会反复提到无后效性的问题。这里不再赘述了。

对最优子结构的举例

[THUWC2020] 报告顺序

Yazid 要听 $n$ 个报告，每个报告有三个整数属性 $a,b,c$，表示当兴奋度为 $x$ 时，听完这个报告后兴奋度变成 $a|x|+bx+c$，Yazid 初始兴奋度为 $s$，Yazid 可以任意安排报告顺序，求听完兴奋度最大是多少。

$|a|, |b|, |c|, |s|, n \leq 15$。

设 $f_S$ 表示听完集合 $S$ 的报告后的兴奋度的最大值。考虑

\[f_S =\max_u\{a_u|f_{S \setminus \{u\}}|+b_uf_{S \setminus \{u\}}+c_u\} \]

这个式子并不正确。这是因为 $g(x) = a_u|x| + b_ux + c_u$ 并不是一个单调函数。并不一定 $x$ 越大，函数值越大。

这便是没有满足最优子结构。

通过分析绝对值函数的性质，我们得知要想获得听完 $S$ 的最大值，需要的不仅仅是 $S \setminus \{u\}$ 的最大值，也有可能是最小值和 $> 0$ 的最小值，$< 0$ 的最大值。

而要想把这个过程持续下去很多轮，我们便也要维护出 $g_S, h_S, r_S$ 表示听完集合 $S$ 的报告后的兴奋度的最小值，听完集合 $S$ 的报告后的兴奋度 $>0$ 的中的最小值，听完集合 $S$ 的报告后的兴奋度的 $<0$ 的中的最大值。

但是为了求出 $> 0$ 的最小值和 $< 0$ 的最大值，后面又不封闭了。这是由于 $c_u$ 导致的偏移。所以我们还要维护 $> -c_u$ 的最小值和 $< -c_u$ 的最大值，为了维护它我们又要维护 $> -c_u - c_v, < -c_u - c_v$，以此类推。

但我们发现 $|c_u|$ 很小，所以我们把有可能通过不断偏移导致最后变为极值的 $[-\sum |c_u|, \sum |c_u|]$ 的可达性全部维护即可。

时间复杂度：$O(2^nn^2|c|)$。

递推与动态规划

在英语中，递推和递归是同一个词 recursion。仅仅指把问题分解为子问题的过程。

在 OI 中，递推问题出现的很多。这是因为递推需要不重不漏地计算，而动态规划只需要不漏。这很考验选手对题目性质的完整把握。

下文中某些部分需要区分动态规划和递推，某些方法是两者共用的。

建模

转移方向

无论是动态规划还是递推，都有拆分为子问题，从子问题那里拿答案的过程。

对于一个具体问题，如何找到合适的状态与转移，使得我们把问题拆分成了子问题，并且可以很好地从子问题中拿答案，并不是一件易事。

这要求我们对问题的结构有深刻的理解。这也就是为什么动态规划和递推如此爱考。这里会有很多高难度题。

一个突破点在于，我们总是要保证无后效性。也就是说，被拆散的部分不能影响剩余的部分。更通俗地说，我们想要这个子问题“封闭”。

UOJ#22 【UR #1】外星人

给定 $n$ 个数 $a_1, a_2, \ldots, a_n$ 和 $x$，对排列 $p$ 考虑依次执行 $x = x \bmod a_{p_i}$，求最后能得到的最大的 $x$ 的值以及这样的排列 $p$ 的个数。

$n \leq 1000$，$x, a_i \leq 5000$。

我们直接来做第二问。

发现只有排列的前缀最小值会起到作用。

所以每次转移考虑转掉一段。

设 $f_i$ 表示 $x=i$ 时，面对所有 $\leq i$ 的 $a$ 时的结果最大值与方案数。

考虑下一个是 $a_k$ 的话，那些介于 $(j \bmod a_k, j]$ 的 $a$ 是无效的，因此摆放位置是随意的。乘以 $\frac{(N_j - 1)!}{N_{j\bmod a_k}!}$。这样我们一次转移到 $f_{j \bmod a_k}$。

时间复杂度 $O(nx)$。

P6295 有标号 DAG 计数

求 $1 \sim n$ 个点有标号的有向无环弱联通图的个数。

$n \leq 10^5$。

考虑先求出任意有标号 DAG，然后对 EGF 求一下多项式 $\ln$ 即可得到弱连通的 DAG 数量。

设 $f_i$ 表示 $i$ 个点的 DAG 数量，考虑每次把所有入度为 $0$ 的点全部删去得到一个子 DAG。

为什么要删去度数为 $0$ 的点？因为这样可以把 DAG 分解为子 DAG。

为什么不一个一个删去入度为 $0$ 的点？因为如果我们在状态里只保留点的数量，那么一个个删去就会产生后效性。

因为所有合法的删除序列是与图的结构相关的，并不能同时转移。我们按图的结构来进行某种划分是困难的。

由于我们不好把握恰好有多少入度为 $0$ 的点，所以容斥一下

\[f_i = \sum_{j=1}^i (-1)^{j-1} \binom ij 2^{j(i - j)}f_{i - j} \]

表示至少有 $j$ 个点度数为 $0$，容斥系数 $(-1)^{j-1}$，这 $j$ 个点到剩下的 $i-j$ 个点连不连边是自由的。

之后用多项式技巧优化即可。

贡献顺序

有时我们需要将题目中的贡献使进行形式的转化，使其变得无后效性。

这可能是式子本身的化简、展开，也有可能是操作过程的视角转换，也可能是贡献的延迟统计，等等等等......总得来说，我们要关注的是贡献在转移过程中的出现顺序。这里的顺序有 order、时效的意思。

实际上在这里很容易同时包括上一部分。因为我们可能会因此改变我们的阶段划分。

Luogu P2612 [ZJOI2012] 波浪

一个 $1\sim n$ 的排列 $P$ 的代价为

\[\sum_{i=1}^{n-1} |P_i-P_{i+1}| \]

求代价 $\leq M$ 的 $P$ 的概率。

$n \leq 100$。

我们将绝对值拆开，有

\[\begin{aligned} &\hphantom{{}={}} \sum_{i=1}^{n-1} |P_i-P_{i+1}| =\sum_{i=1}^{n-1} (P_i-P_{i+1}) \textrm{sgn}(P_i-P_{i+1}) \\ &=P_1\textrm{sgn}(P_1-P_2)+P_n\textrm{sgn}(P_{n-1}-P_n)+\sum_{i=2}^{n-1} P_i (\textrm{sgn}(P_i-P_{i+1})+\textrm{sgn}(P_{i-1}-P_i)) \end{aligned}\]

这样我们就可以对每个数考虑与其相邻的是小于还是大于它来确定它的贡献倍数，这样其绝对位置是不重要的，重要的仅仅是相邻的大小关系。

我们可以在放入一个数时考虑其贡献。考虑从小往大插入数。

设 $f_{i, j, k, l}$ 表示前 $1$ 到 $i$，连成了 $j$ 个连通块，目前统计到的总贡献为 $k$，有 $l$ 个边界被用了的方案数。

考虑插入 $i$ 时，有几个数与其相邻，以及是否与边界相邻。有以下几种情况。

一边与边界相邻，一边不与已经存在的连通块相邻，这会产生一个新的连通块，贡献 $-1$ 倍，方案数 $2-l$。
一边与边界相邻，一边与已经存在的连通块相邻，这不会导致连通块数改变。贡献 $1$ 倍，方案数 $2-l$，要求 $j \neq 0$。
两边与两个已经存在的连通块相邻，这会导致连通块合并，因此连通块数减一。贡献 $2$ 倍，方案数 $j-1$，要求 $j \geq 2$。
两边不与已经存在的连通块相邻，这会导致新增一个连通块，因此连通块数加一。贡献 $-2$ 倍，方案数 $j+1-l$。
一边与已经存在的连通块相邻，另一边不与已经存在的连通块相邻，这不会导致连通块数改变。贡献 $0$ 倍，方案数 $2j - l$。

答案便是 $\frac 1{N!}f_{N, 1, \geq M, 2}$。

Luogu P7213 [JOISC2020] 最古の遺跡 3

有 $2\times N$ 个石柱，对于 $1\le k\le N$ 均有两个石柱高度为 $k$，第 $i$ 个石柱的高度为 $h_i$。

接下来会发生 $N$ 次地震，每次地震会使一些石柱的高度减一，其他石柱高度不变。石柱 $i$ 地震时高度不变，当且仅当 $h_i\ge 1$ 并且对于 $j>i$ 都要有 $h_i\not=h_j$。$N$ 次地震后，恰好只剩下了 $N$ 个石柱。现在给定 $N$ 个石柱的位置 $A_1,A_2,\ldots,A_N$，求最初 $2\times N$ 个石柱高度的方案数 $\bmod~10^9+7$ 的值。

$N \leq 600$。

我们考虑一个位置能够被留住的条件。可知其只与这个位置后面的数有关。如果当前位置为 $x$，而后面会有 $x \sim x - k$，则 $x$ 会下降到 $x - k - 1$。

那么我们可以得到一个算法，给定 $h$，得到 $A$：初始时令一个序列 $B$ 全为 $0$。$i$ 从 $2N$ 到 $1$ 降序枚举，考虑将 $h_i$ 加入序列 $B$，从 $h_i$ 到 $1$ 枚举 $j$，若 $B_j$ 为 $0$，则在这里填入 $i$。如果没有这样的位置，则其不在 $A$ 中。最后便是 $A_{B_i} = i$。

所以每个位置是否存活取决于 $\textrm{mex}\ B$ 与 $h_i$ 的大小关系。我们可以由此得到一个递推做法。

设 $f_{i, j}$ 表示 $2N$ 到 $i$，$\textrm{mex}=j+1$ 的方案数。则答案为 $f_{1, N}$。

若 $i$ 没有在 $A$ 中出现过，则 $j\geq h_i$，$\textrm{mex}$ 不会改变。有

\[f_{i, j}\leftarrow cf_{i+1, j} \]

其中 $c$ 为 $[1, j]$ 中可以放的数字个数，等于 $j - (2N-i - s)$，$s$ 为 $[i + 1, 2N]$ 中存活的位置的个数。为了能够这样统计，我们需要将 $h$ 相同的两个元素当作有标号的，最后将答案除以 $2^n$。否则会需要更多的信息才能算出这里的 $c$。

若 $i$ 出现过，且没有改变 $\textrm{mex}$，我们将它的贡献后延，直到 $\textrm{mex}$ 改变时统计。

\[f_{i, j} \leftarrow f_{i+1, j} \]
若 $\textrm{mex}$ 改变了，考虑新的 $\textrm{mex}=j+k$，则现在需要在那些后延了贡献的位置中选出 $k-1$ 个。这些位置需要满足
- $\leq j+s$ 的数不得超过 $s$ 个。否则就会有人走到 $0$。
- 每个数都不超过 $j+k$。

发现这个过程其实和 $j$ 无关。设辅助数组 $g_k$ 表示 $1, 1, 2, 2, \ldots, k, k$ 这些数选出 $k$ 个，满足 $\leq s$ 的数不得超过 $s$ 个的方案数。$g$ 该怎么求呢？其实和 $f$ 的想法是类似的。只不过现在没有第一种（不在 $A$ 中出现）的情况了。考虑最后一个插入的数显然不会后延，假设其最终到了 $x + 1$，那么它最初有可能是 $[x + 1, k]$，$x + 1$ 还剩两个可选，$[x + 2, k]$ 还剩一个，所以共有 $k-x+1$ 种可能。并且此时前 $x$ 个和后 $k - x - 1$ 个是独立的。我们由此可以得到递推式

\[g_k = \sum_{x=0}^{k-1} \binom{k-1}x g_x g_{k - x - 1}(k - x + 1) \]

\[f_{i, j+k}\leftarrow \sum_{k=j+1}^s \binom {s-j-1}{k-j-1}f_{i+1, j}g_{k-j-1}(k-j+1) \]

时间复杂度 $O(N^3)$。

$\textrm{dp }$套$\textrm{ dp}$

一般是最优化解的计数问题。而前面的最优化问题可以通过动态规划解决。

于是我们有了一个 DAG。在这个 DAG 上递推即可计数。

若有状态 $s$，则设 $F_{s, f_s}$ 表示在状态 $s$ 处取值为 $f_s$ 的方案数。

给定一棵树，每条边的边权等概率为 $1$ 或 $2$，求树的直径的期望。

$n \leq $。

设 $f_u$ 表示最长的从 $u$ 开始的链的长度。

$g_u$ 表示 $u$ 子树的直径长度。

则有：

\[f_u = \max_{u \to v} \{f_v+1\} \]

\[g_u = \max_{u \to v} \{g_v, f_u+f_v+1\} \]

设 $F_{u, i, j}$ 表示 $u$ 号点，$f_u=i, g_u=j$ 的方案数。

去重

在计数递推问题中，经常性地，重复计算的问题需要被考虑。

当题目中的去重方案（或叫等价类划分的方案）和我们所擅长计算的（通常是操作方案）不一致时，我们需要想方设法将其一致。

一个十分常见的想法是同一个等价类选一个代表元素，将元素和等价类一一对应，计算代表元素的个数就是计算等价类个数。

CF720D Slalom

一个 $n \times m$ 的网格，其中有 $k$ 个矩形障碍，保证这些障碍不重叠。求从 $(1,1)$ 走到 $(n,m)$，每步只能往右或往上走，不经过任何障碍的方案数。

两种方案被视为不同，当且仅当存在一个障碍，它在第一种方案里被从右侧绕过，而在第二种方案里被从左侧绕过（第一种左，第二种右同理）。

$n, m \leq 10^6, k \leq 10^5$。

我们所熟悉的计数方式是计算走过不同网格的路径条数，而非跨过的障碍的集合个数。

如果是计算路径条数，我们可以设 $f_{i, j}$ 表示第一次走到第 $i$ 列行数为 $j$ 的路径条数。转移形如

\[f_{i, j} = \sum_{k \leq j}[(i-1, k\sim j) \text{无障碍}]f_{i-1, k} \]

考虑跨过了相同障碍集合的路径集合，他们的限制为在某些竖列 $\leq$ 某些给定的数，表示在其上方的障碍；在某些竖列 $\geq$ 某些给定的数，表示在其下方的障碍。

这样，对障碍的限制来说，每个竖列之间是独立的。我们发现，总是存在这样一条代表路径在所有路径的下方：其在每个位置都尽可能取到了最小值。也就是说，我们总是在无法向右走时才考虑向上走，这样的路径总是唯一且低于任意路径的。这样的路径数等于障碍的集合数。

所以我们使用扫描线，加入一个障碍时仅维护上边界上最左一格的值即可。

当 $(i, j-1)$ 是某个障碍的左上角时，

\[f_{i, j} = \sum_{k \leq j}[(i-1, k\sim j) \text{无障碍}]f_{i-1, k} \]

否则当 $(i, j)$ 不是障碍时，

\[f_{i, j}=f_{i-1, j} \]

这样，我们就能不重不漏地统计障碍集合。

这个式子的优化并不在本章讨论范围内，但实际上并不难。

AGC013D Piling Up

一开始有 $n$ 个颜色为黑白的球，但不知道黑白色分别有多少，$m$ 次操作，每次先拿出一个球，再放入黑白球各一个，再拿出一个球，最后拿出的球按顺序排列会形成一个颜色序列，求颜色序列有多少种。答案对 $10^9+7$ 取模。

$n,m\leq 3000$。

我们很容易计算出操作方案数。

设 $f_{i, j}$ 表示 $i$ 次操作后还有 $j$ 个白球的操作方案数。

\[f_{0, 0}=f_{0, 1} = \ldots = f_{0, n} = 1 \]

\[\begin{cases} \begin{aligned} f_{i+1, j-1}\leftarrow f_{i, j} \\ f_{i+1, j}\leftarrow f_{i, j} \end{aligned} & j \geq 1 \\ \\ \begin{aligned} f_{i+1, j} \leftarrow f_{i, j} \\ f_{i+1, j+1} \leftarrow f_{i, j} \\ \end{aligned} & j < n \\ \end{cases}\]

可以发现，若最初袋中白球数量不同，即使进行相同的操作，每次操作后拿出的球的序列也有可能相同。

也就是说，操作方案与拿出球的序列并不一一对应。

我们发现，对于一个初始状态和一个拿出球的序列，判断其是否是一种合法的操作方案的方式是判断其是否在任意时刻有白球的数量在 $[0, n]$ 之间。那么，我们对这个拿出球的序列计算其与初始状态的白球数量差的最值 $[-a, +b]$，则初始白球的数量在 $[a, n-b]$ 之间是合法的。

我们考虑总是拿出一个代表元素 $a$。那么一个初始状态与操作序列是代表，当且仅当初始袋中再减一个白球会使得操作序列不合法，这等价于在某个时刻袋中有 $0$ 个白球。

所以我们统计在某个时刻袋中有 $0$ 个白球的合法的操作方案数，就等于计算了不同的拿出的球的序列数。

设 $f_{i, j, 0/1}$ 表示 $i$ 次操作后还有 $j$ 个白球，是否碰到过底线 $0$ 的操作方案数。同上转移即可。

优化

简化状态与转移

我们把递推过程视作所有方案分别在有限状态自动机上匹配的过程。

定义有限状态自动机是一个五元组 $M = (Q, \Sigma, \delta, q_0, F)$，其中 $Q$ 表示状态的集合，$\Sigma$ 表示字符集，$\delta:Q \times \Sigma \to Q$（输入是一个二元组 $(q, \sigma)$，输出一个 $Q$ 中的元素）表示转移函数，$q_0$ 表示 $M$ 的（唯一）起始状态，$F \subseteq Q$ 表示终止状态集合。

有限状态自动机从起始状态开始，一个字符接一个字符地读入一个字符串，并根据给定的转移函数一步一步地转移至下一个状态。在读完该字符串后，如果该自动机停在一个属于 $M$ 的接受状态，那么它就接受该字符串，反之则拒绝该字符串。

我们可以把 $Q$ 看作点集，$\delta$ 看作边集，$q_0$ 看作起点，$F$ 看作终点，那么 $M$ 便可以被看作一张有向图。一个被接受的字符串对应着图上一条从起点到某个终点的路径。

在自动机的视角下，递推过程的状态便是其状态，状态间的转移便是其转移，字符集便是这个递推过程的一种推进（子问题拆分的逆过程）。那么每一种合法的方案都对应着自动机上的一条路径。

由此我们也可以理解动态规划与递推的区别。递推要求的是路径的条数，而动态规划则是在这条路径尚未走完时便对其进行取舍，每个状态只保留一条。

根据自动机理论，我们知道每一个有限状态自动机是可以尝试简化的。具体地，对于一个有限状态自动机，如果我们进行

去除多余的状态（死状态）。
将相互等价的两个状态合并。

那么我们会得到一个新的有限状态自动机。这个自动机与原来的自动机是等价的，且是最小的。最小是指不存在一个状态更少的且与其等价的自动机。

当然，在动态规划问题中，还有决策的过程没有被考虑。在取舍的过程中，我们分析出某些状态永远无法被取到或有快速判断其是否无法被取到的方法。这样也可以起到去除无效状态或进行合并的效果。

去除多余的状态

去除多余的状态，即，删去那些不会被起点访问到或是无法走到终点的状态和转移，或是永远无法作为最优解的状态和转移。

一个很经典的技巧是树上背包时，如果我们把所有的循环全部卡紧，复杂度会降到 $O(n^2)$，因为我们可以用组合方法分析复杂度：每一对元素仅会在其 lca 处合并一次。

CF1299D Around the World

给定一张无向联通图，大小为 $n$，有 $m$ 条边，每条边有边权，保证无重边自环。

同时保证，不存在一个长度 $> 3$ 的简单环经过了 $1$ 号点。

你需要求解，有多少种方案删除若干条与 $1$ 号节点相连的边，使得不存在任意一条路径（不一定是简单路径）满足下列 $3$ 个条件：

其以 $1$ 号节点为起点，$1$ 号节点为终点。
此路径经过的所有边的边权异或和为 $0$。
其至少经过了一条边奇数次。

你需要输出这个方案数对 $10^9+7$ 取模的结果。

$n,m\leq 10^5$，$w\leq 31$。

先考虑不存在经过 $1$ 号点的简单环的情况。

删去与 $1$ 号点相邻的所有边，图被分成了若干个连通块，设其为 $k$ 个。我们知道，如果想要凑出一条非法路径，需要在每个连通块中走一些环，使得异或和为 $0$。我们可以提前算出每个连通块能够凑出的异或值的集合 $T$。

设 $f_{i, S}$ 表示前 $i$ 个连通块中走能够走出的异或值集合为 $S$ 的方案数。每次加入一个新的集合 $T$ 时有

\[f_{i+1, S \oplus T} \leftarrow f_{i, S} \]

其中 $S \oplus T=\{s \oplus t|s \in S, t \in T\}$。

这样的状态数是 $k2^w$。

但我们知道，并非所有的状态都有值。因为若 $a \in S, b \in S$，则 $a \oplus b \in S$。不满足这一条的状态，一定不会有值。

我们把所有不满足这一条的状态删去，剩下的状态便为本质不同的线性空间。通过搜索+线性基可以求得仅有 $374$ 种。

也就是说，仅有这 $374$ 个位置是有值的。我们仅保留这些状态，可以大大优化算法复杂度。

同时我们可以通过线性基提前预处理出他们之间的 $\oplus$ 转移关系进行加速。

有三元环的情况是平凡的：如果不使用这个环，那么可以有两种方式走到这个连通块，故转移系数多一个 $\times 2$；若使用了这个环，则线性基里多一个元素表示走这个环。

想要意识到有效状态极少，我们要对线性空间的结构有所理解，才能意识到它的要求有多么严格，从而意识到绝大多数的状态都是不合法的。

我们可以定量分析。假设我们要在大小为 $2$ 的域上的 $n$ 维线性空间选取 $k$ 个线性无关的向量，第一个可以任取，方案为 $2^n-1$；第二个只能取与第一个线性无关的向量，方案为 $2^n-2$；第三个不能取与前两个线性相关的向量，方案为 $2^n-4$，以此类推，总方案数为

\[\prod_{i=1}^k (2^n-2^i) \]

但这样会重复计数。因为同一个线性空间有多组基可以表示，其方案数为 $k$ 维线性空间选取 $k$ 个线性无关的向量的方案数，为

\[\prod_{i=1}^k (2^k-2^i) \]

故线性空间的个数为

\[\frac{\prod_{i=1}^k (2^n-2^i)}{\prod_{i=1}^k (2^k-2^i)}=\frac{\prod_{i=n-k+1}^n (2^i-1)}{\prod_{i=1}^k (2^i-1)}={n\brack k}_2 \]

其中 ${n\brack k}_q$ 为高斯二项式系数。数量级在 $O(q^{k(n-k)})$。

在本题中为 $\sum_{i=0}^5 {5 \brack i}_2=374$。

合并等价状态

我们先要知道如何刻画状态的等价性。

根据自动机理论，如果两个状态在同时接受任意相同字符串后要么同时到达终态，要么同时不到达终态，则两个状态等价。

这样的定义是十分显然的。因为我们并不能通过任何输入来区别两个点，所以它们被视作一个状态。

在递推类问题中，如果两个状态对今后子问题的贡献完全相同，那么我们可以将其合并为一种状态。

还有一种情况。如果两个状态在目前的阶段还无法被区分，或是拥有类似的转移，那么就可以先把两者当作同一种状态，或是用数据结构更快速地维护以降低复杂度。此之谓 “整体 dp”。

AGC017F Zigzag

给定一个 $N$ 层的三角形图，第 $i$ 层有 $i$ 个节点。第 $i$ 层的节点，从左到右依次标号为 $(i, 1), (i, 2), \ldots, (i, i)$。

你需要从 $(1, 1)$ 往下画 $M$ 条折线。对于每条折线的每一个小段，你可以从 $(i, j)$ 画到 $(i + 1, j)$ 或者 $(i + 1, j + 1)$。同时你还必须保证第 $i$ 条折线的任何一个位置必须不能处在第 $i - 1$ 条折线的左侧，它们必须按照从左到右的顺序排列。

有 $K$ 条限制，每条限制形如 $(A_i, B_i, C_i)$。表示第 $A_i$ 条折线处于位置 $(B_i, j)$ 时，下一小段必须走向 $(B_i + 1, j + C_i)$，也就是当 $C_i = 0$ 时向左，当 $C_i = 1$ 时向右。

询问不同的折线画法的方案数，对 $10^9 + 7$ 取模。

$1 \le N, M \le 20$，$0 \le K \le M (N - 1)$。

我们考虑从左到右，依次确定每条折线的形态。

如果直接状压 dp，每次转移一条线，可以做到 $O(4^N\text{poly}(N, M))$。

发现限制是对前缀要求的，所以可以使用轮廓线 dp，每次从上往下加一格。

设 $f_{i, S, j, d}$ 表示前 $i$ 条已经完成，第 $i+1$ 条已经转移了前 $j$ 步，$i+1$ 的前 $j$ 步和 $i$ 的后 $N-j$ 步凑成了 $S$，第 $i$ 条在目前的水平坐标是 $d$ 的方案数。

这样每次转移是 $O(1)$ 的，总复杂度就是状态数 $O(2^NMN^2)$。

但是我们发现，目前这条路径能够走到的应该是一个锥形。我们将其与上一条路径提供的限制取交，发现其和一条从目前的 $j$ 出发的路径限制等价。

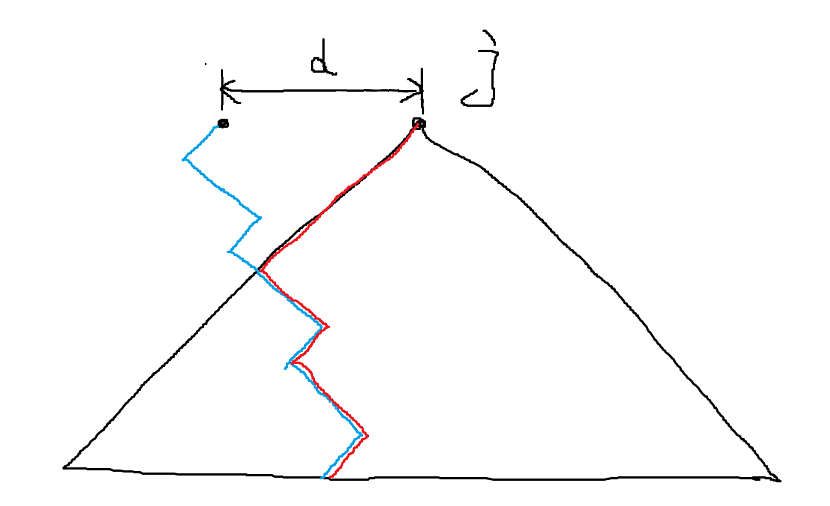
如图，每一个蓝色的路径都会和一个棕色路径等价。

所以我们可以把所有形如蓝色的 $f$ 全部合并为一个状态。具体来说就是不记录 $d$，而是每次把 $S$ 的从 $j+1$ 开始的第一个 $1$ 改成 $0$。这就把状态数省去了一个 $N$。

LOJ#553. 「LibreOJ Round #8」MINIM

取石子游戏的规则是这样的：有若干堆石子，两个玩家轮流操作，每个玩家每次要选一堆取走任意多个石子，但不能不取，无石子可取者输。

现在共有 $n$ 堆石子，其中第 $i$ 堆的数量为 $l_i$，你现在需要在每一堆里选若干个石子。只要第 $i$ 堆被选了至少一个，就要花费 $v_i$ 的代价。

有 $q$ 次询问，每次给出一个 $c\in [0,m]$，表示再新加一堆，石子数为 $c$。求付出代价的总和至少是多少，使得用这些被选出的石子和这新加的一堆进行一次取石子游戏，后手必胜。

$n, q \leq 10^5$，$m \leq 10^9$，$l_i, v_i$ 在 $10^9$ 内均匀随机。

CF506E Mr. Kitayuta's Gift

给定一个小写字符串 $s$ 和一个正整数 $n$。要求在 $s$ 中插入恰好 $n$ 个小写字符使其回文的方案数。

两个方案不同当且仅当它们得到的串不同，与插入顺序和位置无关。

$|s| \leq 200$，$n \leq 10^9$，答案对 $10^4 + 7$ 取模。

题目要求的是不同的字符串个数，而不是操作数。所以我们考虑直接考虑这个回文串的形态。如果有一个回文串 $T$，我们判断其是否能作为答案的算法如下：

最初令 $l=0, r = |s| - 1$。从 $0$ 到 $\frac {|T| - 1}2$ 枚举 $T_i$，如果 $T_i = s_l = s_r$，那么 $l \leftarrow l+1, r \leftarrow r - 1$，否则如果 $T_i = s_l$，$l \leftarrow l + 1$，否则如果 $T_i = s_r$，$r \leftarrow r - 1$。最终我们检查是否有 $l > r$，如果是，则 $T$ 属于答案。

我们可以由此得到一个递推算法。设 $f_{i, l, r}$ 表示此算法进行到这个状态的 $T$ 的个数。终态 $\text{goal}_i$ 表示算法已经执行完毕的 $T$ 的个数。

如果 $s_l = s_r$，则有

\[\begin{cases} f_{i+1, l+1, r-1} \leftarrow f_{i, l, r} \\ f_{i+1, l, r} \leftarrow 25f_{i, l, r} \\ \end{cases}\]

否则有

\[\begin{cases} f_{i+1, l+1, r} \leftarrow f_{i, l, r} \\ f_{i+1, l, r - 1} \leftarrow f_{i, l, r} \\ f_{i+1, l, r} \leftarrow 24f_{i, l, r} \end{cases}\]

最后我们回收

\[\begin{cases} \text{goal}_{i} \leftarrow f_{i, l, l - 1} + f_{i, l, l - 2} \\ \text{goal}_{i+1} \leftarrow \text{goal}_{i} \end{cases}\]

这样每轮的状态数是 $O(|s|^2)$ 的，需要做 $O(n)$ 轮。

在自动机视角下，此题里，一个 $(l, r)$ 就对应着一个状态。填入一个 $T_i$ 就对应着一个操作，在每个状态那里可以得到一个转移。一个合法的 $T$ 就对应着自动机上一条从 $(0, |s| - 1)$ 到 $\text{goal}$ 的路径。于是我们将问题转化为求图上的路径条数。

那么现在考虑用组合的视角来看这个图。每条路径形如在每个点上走许多次自环，之后向前走。如果有 $a$ 个权值为 $24$ 的自环，那么便会有 $b = \lceil \frac{|s| - a}2 \rceil$ 个长度为 $25$ 的自环，其走过非自环边的次数为两者之和。而我们发现，其路径权值和与这些自环权值的顺序是无关的，所以我们可以将 $a$ 相同的全部归为一类。这样我们对每一种 $a$ 使用矩阵加速，复杂度为 $O(|s|^4 \log n)$。

一个观察是 $a$ 不同的图可以合并起来，我们在左侧从起点开始向下连出一个足够长的链，每个点有一个权值为 $24$ 的自环，再在右侧以终点为链尾向上反着连出一个足够长的链，每个点有一个权值为 $25$ 的自环。这样 $(a, b)$ 就可以对应为左侧的正数第 $a$ 个点往右侧倒数第 $b$ 个点连了一条边。这样所有的 $a$ 可以在一次加速中全部算出，复杂度为 $O(|s|^3 \log n)$。

当然，我们可以直接把其组合式列出来并使用组合计数的方法来优化。

分步

有两种分步。

我们上文提到，可能会为了保证无后效性而同时转移掉许多元素。但反之也有可能，如果问题的无后效性非常强，我们可能会尽可能缩小每次转移的规模，降低转移复杂度。

最著名的例子便是轮廓线 dp 了。

第二种是多次转移可能会有重复或相似的部分，我们把他们抽取出来，只用计算一次，便可以加速所有这样的转移。

P5359 [SDOI2019]染色

给定 $2\times n$ 的格点图。其中一些结点有着已知的颜色，其余的结点还没有被染色。

一个合法的染色方案不允许相邻结点有相同的染色。

现在一共有 $c$ 种不同的颜色，依次记为 $1$ 到 $c$。

求有多少对未染色结点的合法染色方案。

$n, c \leq 10^5$。

设 $f_{i, a, b}$ 表示前 $i$ 列，第 $i$ 列染了颜色 $a, b$ 的方案数。转移很简单。

这样的复杂度是 $O(nc^2)$ 的。

考虑颜色是抽象的。所以我们对每个空子段记录具体的颜色信息是过于冗余的。

如果中间有一段 $2 \times m$ 的子段是空的，那么实际上填入的方案数之和其左侧的两个格子，右侧的的两个格子的\textbf{相同关系}有关。

有以下五种情况。


左侧	$\begin{bmatrix}a \\ b\end{bmatrix}$	$\begin{bmatrix}a \\ b\end{bmatrix}$	$\begin{bmatrix}a \\ b\end{bmatrix}$	$\begin{bmatrix}a \\ b\end{bmatrix}$	$\begin{bmatrix}a \\ b\end{bmatrix}$
右侧	$\begin{bmatrix}a \\ b\end{bmatrix}$	$\begin{bmatrix}b \\ a\end{bmatrix}$	$\begin{bmatrix}a \\ c\end{bmatrix}$	$\begin{bmatrix}b \\ c\end{bmatrix}$	$\begin{bmatrix}c \\ d\end{bmatrix}$

设 $g_{1 \sim 5, i}$ 表示这种情况下，长度为 $i$ 的空子段的方案数。

这样我们就不用对空子段记录 $c^2$ 中状态了。

设 $f_{i, a}$ 表示在一个非空的列 $i$，那个没填的位置是 $a$ 的方案数。如果这一列两行都填了那就默认 $f_i$ 只有一个位置有值。

用 $g$ 辅助，每次从一个非空列转移到一个非空列。

可以用数据结构做到 $O(n+c)$。

杂项

带权二分
矩阵加速
斜率优化
决策单调性
组合计数方法
其他

不难，自己悟。


左侧	\(\begin{bmatrix}a \\ b\end{bmatrix}\)	\(\begin{bmatrix}a \\ b\end{bmatrix}\)	\(\begin{bmatrix}a \\ b\end{bmatrix}\)	\(\begin{bmatrix}a \\ b\end{bmatrix}\)	\(\begin{bmatrix}a \\ b\end{bmatrix}\)
右侧	\(\begin{bmatrix}a \\ b\end{bmatrix}\)	\(\begin{bmatrix}b \\ a\end{bmatrix}\)	\(\begin{bmatrix}a \\ c\end{bmatrix}\)	\(\begin{bmatrix}b \\ c\end{bmatrix}\)	\(\begin{bmatrix}c \\ d\end{bmatrix}\)

526互联

OI 中常见的 dp 与递推问题的大致分类