多边形绘制算法

通常用多边形近似表示物体，多边形的表面绘制一般用扫描线实现. 而将光照模型应用于表面绘制，称为明暗处理. 明暗处理一般仅计算顶点的表面光强度，多边形面的其他位置通过插值得到. 因此，明暗处理又称为光亮度插值.
为解决多个平面近似表示的曲面物体的绘制物体问题，提出了不同的简便算法，典型：Gouround光亮度插值、Phong向量插值.

恒定强度的明暗处理

恒定强度表面绘制（constant-intensity surface rendering）或平面绘制（flat surface rendering）：为所有投影点赋予相同的颜色 —— 将多边形表面一个顶点或中心点的光照模型应用于表面每个点，继而计算RGB三颜色分量.

特点：快速、简单，快速生成一般曲面的大致外观. 但适用条件苛刻.

适用条件（and）：

多边形是多面体的一个面，且不是一个近似表示曲面的多边形网的一部分；
所有（照明该多边形的）光源离对象表面足够远，以至于N·L与衰减函数对于对象表面是各常数（见计算机图形：光照模型的Lambert漫反射模型、辐射强度衰减部分）；
视点离该多边形足够远，以至于V·R对于多边形是一个常数.

注：N：物体表面单位法向量；L：入射点到光源的单位向量，N·L：入射角余弦值；V：入射点到视点的单位向量；R：反射光线的单位向量.

Gouraud明暗处理

概述

Gouraud表面绘制（Gouraud Surface rendering）又称为光强度插值表面绘制（intensity-interpolation surface rendering）：将曲面表面的光亮度取为近似表示该曲面的各个多边形顶点的双线性插值.

优点：光强度沿相邻多边形的公共边界均匀过渡，消除了在平面绘制中的光强度不连续的现象.
缺点：表面上的高光有时会出现异常形状，如表面出现过亮或过暗的条纹，称为马赫带（Mach band）效应.
解决缺点的办法：1）使用更细小的多边形分割；2）使用其他明暗处理算法，如Phong明暗处理.

步骤：
1）确定每个多边形顶点处的平均单位法向量；
2）对每个顶点，应用光照模型计算光强度；
3）在多边形投影区域对顶点光强度进行线性插值；

对于1），求顶点单位法向量，常见空间曲线、曲面的法向量求解参见计算机图形：计算法向量.
例如，以A为公共顶点的4个相邻多边形的单位法向量分别为$\bm{N_1、N_2、N_3、N_4}$，则A点处单位法向量：

\[\bm{N_A}=\frac{\bm{N_1+N_2+N_3+N_4}}{4} \]

tips: 计算顶点单位法向量前，需要计算各多边形法向量并单位化.

对于2），对顶点应用前面讲的光照模型，详见计算机图形：光照模型，计算光强.

对于3），在多边形绘制时，应用扫描线算法进行双线性插值：
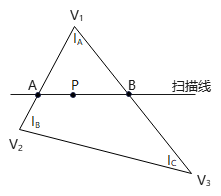
例如，三角形$V_1V_2V_3$中，三顶点光强分别为$I_1,I_2,I_3$. 一扫描线与三角形相交于A、B，P是投影于相应扫描线上一像素中心的多边形采样点，取A点光强$I_A$为$I_1、I_2$的线性插值，B点光强$I_B$为$I_1、I_3$的线性插值. 目的是求出P点光强.

有，

\[\begin{cases} I_A=uI_1+(1-u)I_2, & u=\frac{AV_2}{V_1V_2}\\ I_B=vI_1+(1-v)I_3, & v=\frac{BV_2}{V_1V_3} \end{cases} \]

P点光强$I_P$为A、B两点的线性插值：

\[I_P=tI_A+(1-t)I_B, t=\frac{PB}{AB} \]

其中，u、v、t是插值参数.

为了快速计算插值参数u、v、t，可以先用y坐标计算出A、B点对应的参数u、v，然后再用x坐标算出P点对应的参数t，即

\[u=\frac{y_A-y_2}{y_1-y_2},\\ v=\frac{y_B-y_3}{y_1-y_3},\\ t=\frac{x_B-x_P}{x_B-x_A} \]

tips: A、B同一条扫描线=>$y_A=y_B$.

线性插值公式

线性插值的公式证明参见数学基础：三角形重心坐标插值公式的证明.

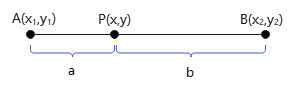
描述见下图，设点P是线段AB的插值点，长度$a=AP,b=BP$，则P:

\[P=uA+(1-u)B,u=\frac{b}{a+b} \]

写成坐标列向量形式：

\[\begin{pmatrix} x\\y \end{pmatrix} =u\begin{pmatrix} x_1\\y_1 \end{pmatrix} +(1-u)\begin{pmatrix} x_2\\y_2 \end{pmatrix},u=\frac{b}{a+b} \]

增量法线性插值

如果对扫描线上每个像素点都应用线性插值求光强，无疑带来大量运算. 可以用增量法，沿着扫描线从左到右计算线段AB上所有像素点的光强. 对每个像素点，仅用一次加法运算.

先说结论. 设$I_A,I_B$已确定，点$P_1,P_2$是扫描线上相邻2像素坐标，相邻像素的插值参数差为Δt，则$P_2$处光强$I_{P2}$与$P_1$处光强$I_{P1}$关系：

\[I_{P2}=I_{P1}+(I_A-I_B)Δt=I_{P1}+ΔI \]

其中，ΔI在同一条扫描线上为常数，即一条扫描线需要计算一次.

下面证明该关系式：
由$P_1,P_2$是线段AB的插值，可知，

\[\begin{cases} I_{P1}=u_1I_A+(1-u_1)I_B,&u_1=\frac{P_1B}{AB}=\frac{x_B-x_{P1}}{x_B-x_A}\\ I_{P2}=u_2I_A+(1-u_2)I_B,&u_2=\frac{P_2B}{AB}=\frac{x_B-x_{P2}}{x_B-x_A} \end{cases} \]

其中，$u_1,u_2$是插值参数，取决于$P_1,P_2$对线段AB的分比，即取决于它们的位置.

做减法，可得，

\[I_{P2}-I_{P1}=(u_2-u_1)I_A-(u_2-u_1)I_B=(u_2-u_1)(I_A-I_B) \]

令$Δt=u_2-u_1$，则$I_{P2}-I_{P1}=(I_A-I_B)Δt$

问题转化为需要证明：1）$Δt$是常数；2）$I_A-I_B$是常数.

∵$P_1,P_2$是同一条扫描线上相邻像素点
∴$x_{P2}-x_{P1}=1$是常数
∴$Δt=u_2-u_1=\frac{1}{x_B-x_A}$是常数

∵三角形是确定的，扫描线也是确定的
∴每条扫描线上的A、B点是确定的（相对于$P_1,P_2$点）
∴$I_A,I_B$是确定的(由2个方向上的一次线性插值得到)
∴$I_A-I_B$是确定的

故得证.

Phong明暗处理

概述

Phong表面绘制（Phong surface rendering），又称法向量插值绘制（normal-vector interpolation rendering）：对多边形顶点处法向量进行插值，取代光强度插值.

优点：多边形内部法向量变化连续，光强度更精确计算、更真实的表面高光显示，能有效解决马赫带效应问题.
缺点：需要比Gouraud更多的计算.

tips：时间换真实感效果.

类似于前面的光强度插值，法向量插值也能用扫描线的双线性插值法，求出多边形内扫描线上每个点的法向量，然后再应用光照模型求出各点光强度.

双线性插值求法向量

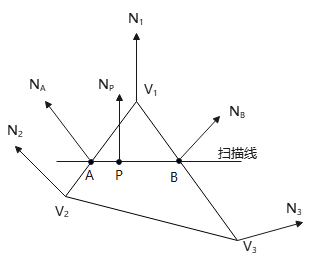
举个例子，设$V_1,V_2,V_3$点的法向量分别为$N_1,N_2,N_3. 设A点法向量$N_A$为$N_1,N_2$的线性插值，B点的法向量$N_B$为$N_1,N_3$的线性插值，那么位于扫描线的线段AB的插值点P处的法向量$N_P$是多少？

对A、B应用线性插值：

\[\begin{cases} N_A=uN_1+(1-u)N_2,& u=\frac{AV_2}{V_1V_2}\\ N_B=vN_1+(1-u)N_2,& v=\frac{BV_3}{V_1V_3} \end{cases} \]

再对P应用线性插值：

\[N_P=tN_A+(1-t)N_B,\space t=\frac{PB}{AB} \]

其中，u、v、t为插值参数.

增量法线性插值求法向量

在上例基础上，在同一条扫描线上，对AB之间的像素点应用增量法求法向量：

\[N_{P2}=N_{P1}+(N_A-N_B)Δt=N_{P1}+ΔN \]

其中，$P_1,P_2$是从线段AB的相邻点，ΔN是相对于扫描线的常数.

快速Phong明暗处理

Phong明暗处理计算量大，可采用一些加速方法，有2类：数值法，几何法.

一种常用优化方法：隔一个像素应用光照模型，中间像素光强度取相邻像素的平均值.

另一种数值优化方法：将法向量插值公式代入光照模型，取泰勒展开式前3项近似作为光强度计算的公式. 也就是本文的快速Phong明暗处理.

快速Phong表面绘制（Fast Phong surface rendering)利用泰勒扩展式（Taylor series expansion）和三角形面片近似计算光强度.

三角形中，对任一点(x,y)的表面法向量N进行插值，可表示为：

\[\bm{N}=\bm{A}x+\bm{B}y+\bm{C} \]

其中，

\[\begin{aligned} \bm{A}&=a_1\bm{N_2}+a_2\bm{N_3-(a_1+a_2)}\bm{N_1}\\ \bm{B}&=b_1\bm{N_2}+b_2\bm{N_3-(b_1+b_2)}\bm{N_1}\\ \bm{C}&=c_1\bm{N_2}+c_2\bm{N_3-(1-c_1-c_2)}\bm{N_1} \end{aligned} \]

设$\bm{L}$是三角形面片的入射光线反向的向量（入射点指向点光源），则漫反射因子：

\[\begin{aligned} E_d(x,y)&=\frac{\bm{L}\cdot \bm{N}}{|\bm{L}| |\bm{N}|}\\ &=\frac{\bm{L}\cdot (\bm{A}x+\bm{B}y+\bm{C})}{|\bm{L}| |\bm{A}x+\bm{B}y+\bm{C}|}\\ &=\frac{\bm{L}\cdot \bm{A}x + \bm{L}\cdot \bm{B}y + \bm{L}\cdot \bm{C}}{|\bm{L}| |\bm{A}x+\bm{B}y+\bm{C}|}\\ &=\frac{ax+by+c}{\sqrt{dx^2+exy+fy^2+gx+hy+i}} \end{aligned} \]

其中，

\[\begin{aligned} a&=\frac{\bm{L}\cdot \bm{A}}{|\bm{L}|},B=\frac{\bm{L}\cdot \bm{B}}{|\bm{L}|},c=\frac{\bm{L}\cdot \bm{C}}{|\bm{L}|},\\ d&=\bm{A}\cdot \bm{A}, e=2(\bm{A}\cdot \bm{B}), f=\bm{B}\cdot \bm{B},\\ g&=2(\bm{A}\cdot \bm{C}),h=2(\bm{B}\cdot \bm{C}),i=(\bm{C}\cdot \bm{C}) \end{aligned} \]

将漫反射因子$E_d(x,y)$在(0,0)处按二元泰勒级数展开，取前三项，可得

\[E_d(x,y)=T_5x^2+T_4xy+T_3y^2+T_2x+T_1y+T_0 \]

其中，每个$T_k$都能用参数a,b...i表示.

\[\begin{aligned} T_5&=\frac{3ig^2-4cdi-4agi}{8i^2\sqrt{i}},T_4=\frac{3cgh-2cei-2bgi-2ahi}{4i^2\sqrt{i}},\\ T_3&=\frac{3ch^2-4cfi-4bhi}{8i^2\sqrt{i}},T_2=\frac{2ai-cg}{2i\sqrt{i}},\\ T_1&=\frac{2bi-ch}{2i\sqrt{i}},T_0=\frac{c}{\sqrt{i}} \end{aligned} \]

递推关系：假设屏幕上像素计算顺序为$(x_0,y_0),(x_1,y_1),...,(x_k,y_k),...,(x_{k+1}-x_{k}=l,y_{k+1}-y_{k}=l)$，其中l是常数，那么，

\[E_d(x_{k+1},y_{k+1})=2E_d(x_k,y_k)-E_d(x_{k-1},y_{k-1})+T \]

其中，T是常数. 这样，计算每个像素的漫反射因子仅仅需要2次加法、1次移位运算.

同理，可根据$E_s=\frac{\bm{N}\cdot\bm{H}}{|\bm{N}||\bm{H}|}$求出镜面反射因子.