6.1 堆及堆的性质
(二叉)堆可以看作完全二叉树,其存储结构通常是数组,表示堆的数组A中有两个重要属性:\(A.length\)表示数组元素的个数;\(A.heap-size\)表示有多少个堆元素在数组中,\(0 \le A.heap-size \le A.length\)。
假设树的根结点为\(A[1]\),给定一个结点的下标\(i\),可以得到其父结点、左孩子和右孩子的下标:

PARENT(i) return i >> 1
LEFT(i) return i << 1
RIGHT(i) return i << 1 | 1
// 在堆排序好的实现中,这三个函数通常是以宏或者内联函数实现的。
二叉堆的两种形式:大根堆和小根堆
- 大根堆:最大元素在堆顶,除根结点外的所有结点\(i\)满足\(A[PARENT(i)] \ge A[i]\)
- 小根堆:最小元素在堆顶,除根结点外的所有结点\(i\)满足\(A[PARENT(i)] \le A[i]\)
本章中的堆排序以大根堆为例,优先队列以小根堆为例。
6.2 维护堆的性质
维护堆的性质(又称整堆):设有数组\(A\)和结点\(i\),假定根结点为\(LEFT(i)\)和\(RIGHT(i)\)的二叉树都是大根堆,但\(A[i]\)可能小于其孩子结点,因此要对结点\(A[i]\)进行整堆,使其重新满足大根堆的性质。

上面算法的思想是:找出结点\(i\)和左右孩子结点中的最大值,交换结点\(i\)和最大值结点,然后递归地向下调用方法,传入下方被交换位置的结点索引。
下图展示了MAX-HEAPIFY的执行过程。
MAX-HEAPIFY的时间复杂度是\(\Omicron(h)\),\(h\)为树高。
6.3 建堆
我们可以自下而上的调用MAX-HEAPIFY方法将数组\(A[1..n]\)构建成大根堆。子数组\(A[\lfloor \frac{n}{2} \rfloor + 1..n]\)中的元素都是叶结点,每个叶结点都可以看成包含一个元素的堆,只需对\(A[1..\lfloor \frac{n}{2} \rfloor]\)的结点进行整堆操作。
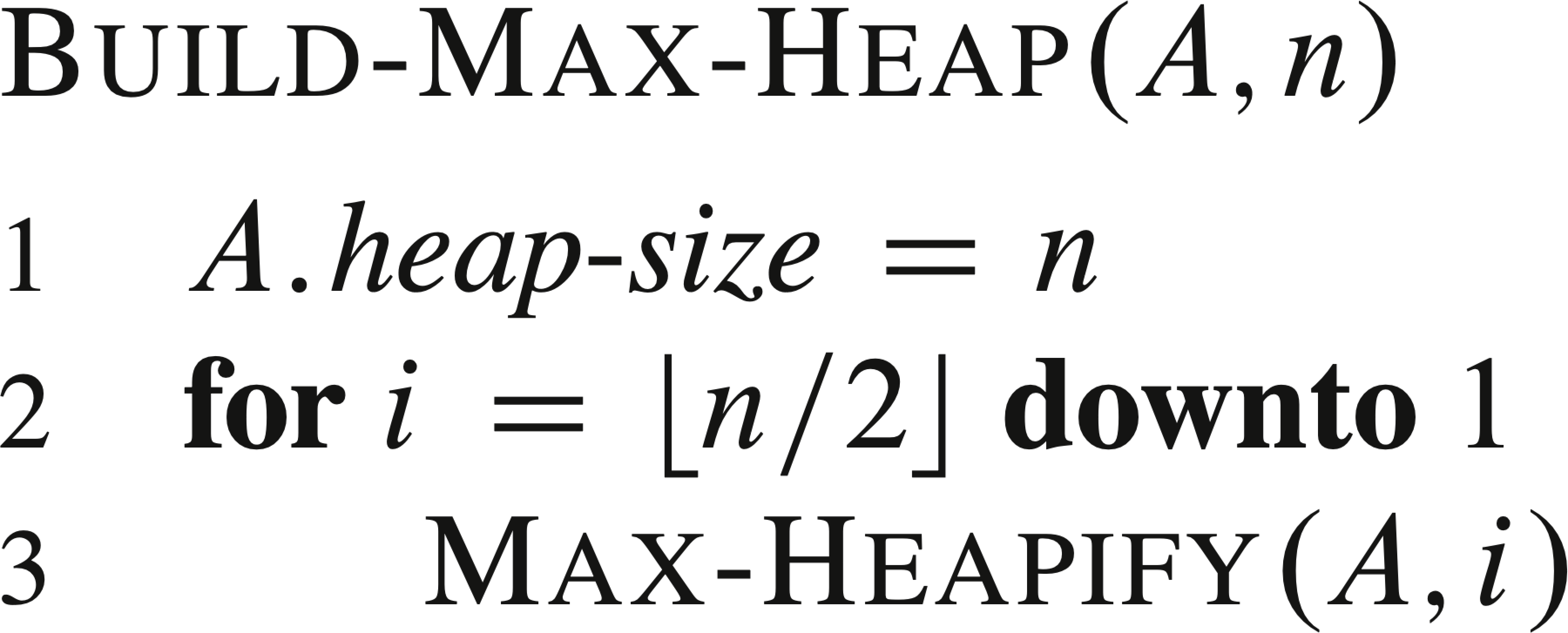
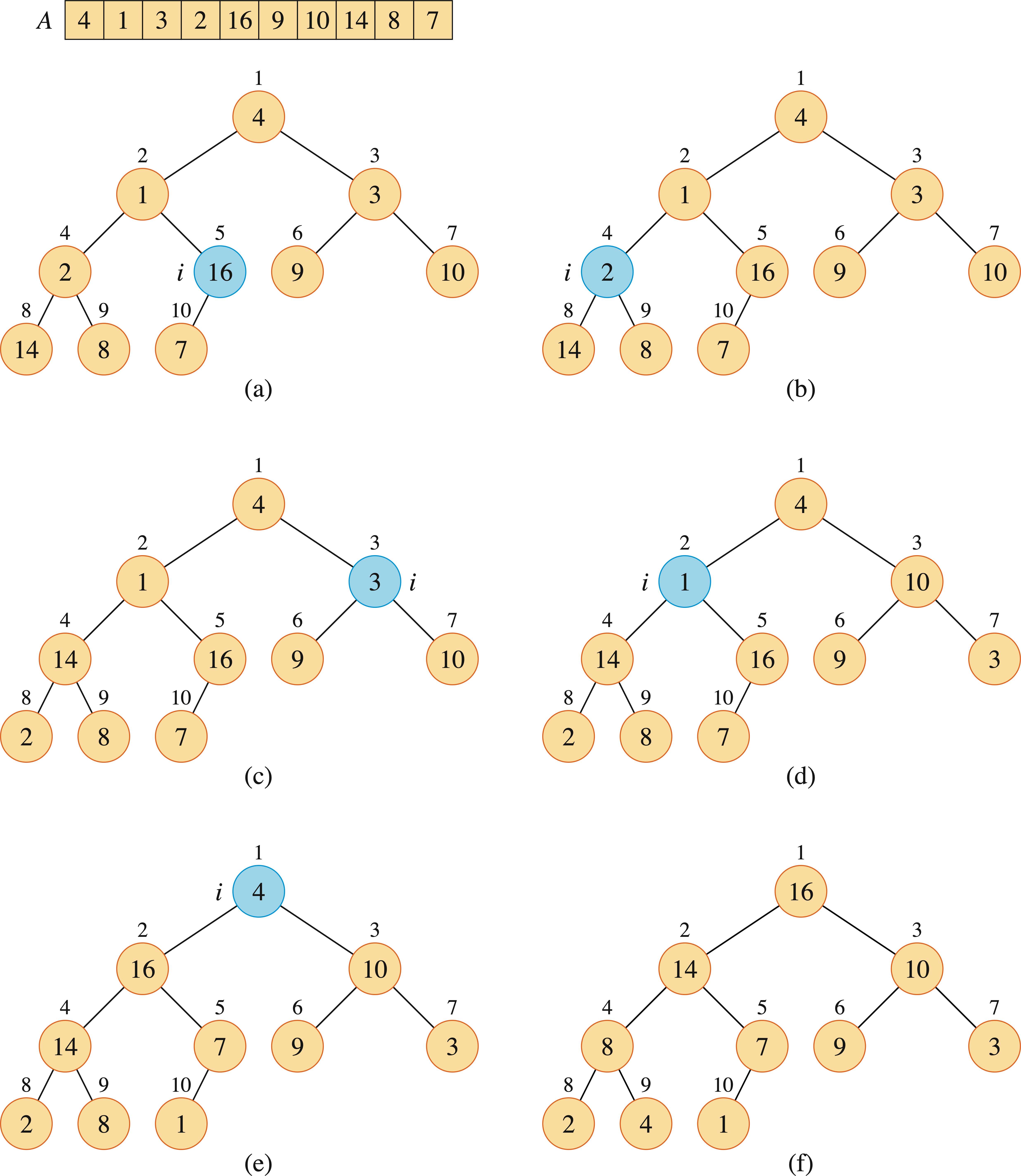
我们可以在线性时间\(\Omicron(n)\)内,把一个无序数组构造称为一个大根堆。
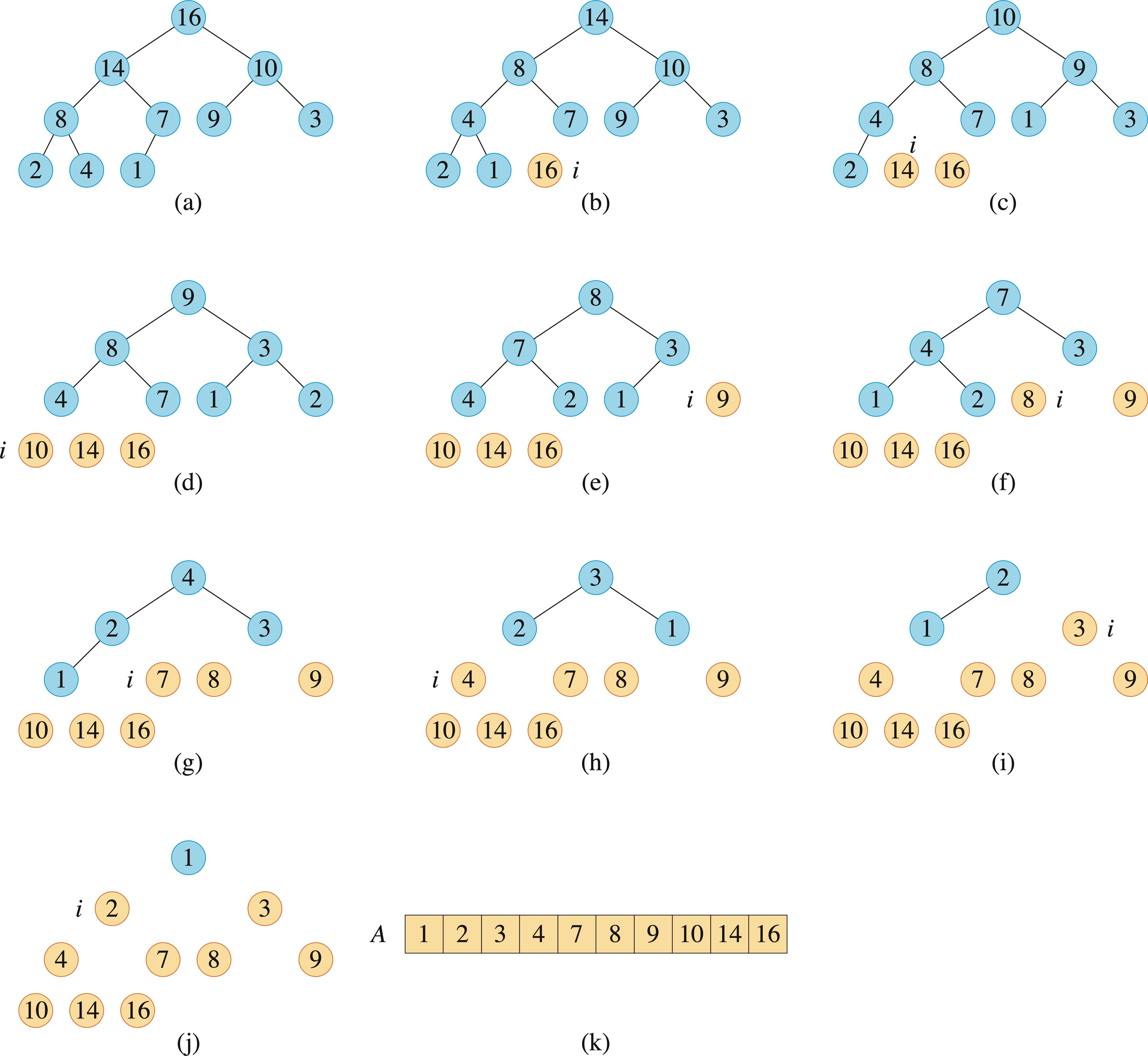
6.4 堆排序
算法思想:初始时,利用BUILD-MAX-HEAP将输入数组\(A[1..n]\)建成大根堆,其中\(n=A.length\)。因为数组中的最大元素总在根结点\(A[1]\)中,通过把它与\(A[n]\)进行互换,从堆中去掉结点\(n\)(这一操作可以通过减少\(A.heap-size\)的值来实现),在剩余的结点中,因为互换,新的结点可能会违背最大堆的性质,因此需要进行整堆操作,调用MAX-HEAPIFY(A, 1),从而在\(A[1..n-1]\)上构造一个新的大根堆。不断重复这一过程,知道堆的大小降到2。
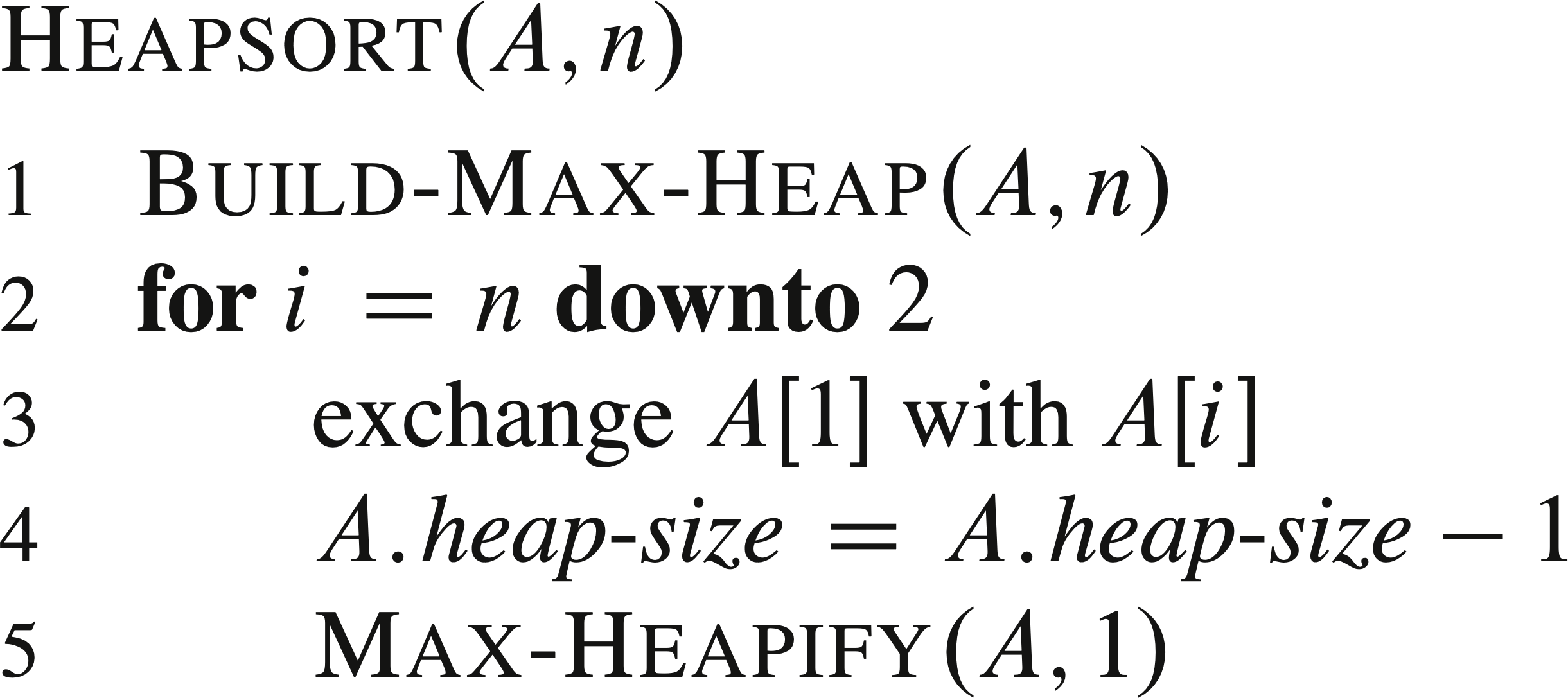
package ch06;
import java.util.Arrays;
public class HeapSort {
private static int heap_size; // 当前堆中的元素
public static int PARENT(int i) {
return ((i + 1) >> 1) - 1;
}
public static int LEFT(int i) {
return ((i + 1) << 1) - 1;
}
public static int RIGHT(int i) {
return ((i + 1) << 1);
}
public static void exchange(int[] arr, int a, int b) { // 交换数组中两个位置的元素
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
public static void MAX_HEAPIFY(int[] A, int i) { // 整堆操作
int l = LEFT(i);
int r = RIGHT(i);
int largest;
if (l + 1 <= heap_size && A[l] > A[i]) {
largest = l;
} else {
largest = i;
}
if (r + 1 <= heap_size && A[r] > A[largest]) {
largest = r;
}
if (largest != i) {
exchange(A, i, largest);
MAX_HEAPIFY(A, largest);
}
}
public static void BUILD_MAX_HEAP(int[] A) { // 建堆操作
heap_size = A.length;
for (int i = A.length / 2 - 1; i >= 0; i--) {
MAX_HEAPIFY(A, i);
}
}
public static void HEAP_SORT(int[] A) { // 堆排序
BUILD_MAX_HEAP(A);
for (int i = A.length - 1; i >= 0; i--) {
exchange(A, 0, i);
heap_size--;
MAX_HEAPIFY(A, 0);
}
}
public static void main(String[] args) {
int[] A = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
HEAP_SORT(A);
System.out.println(Arrays.toString(A));
}
}
堆排序的时间复杂度为 \(\Omicron(n \log n)\)。
6.5 优先队列
尽管快速排序的一般性能要优于堆排序,但堆这一数据结构仍然有很多应用。堆的一个常见应用:优先队列。和堆一样,优先队列也有两种形式:最大优先队列、最小优先队列。
优先队列(priority queue)是一种用来维护由一组元素构成的集合\(S\)的数据结构,其中的每个元素都有一个相关的值,称为关键字(key)。一个最大优先队列支持如下操作:
INSERT(S, x):把元素\(x\)插入集合\(S\)中。MAXIMUM(S):返回\(S\)中具有最大关键字的元素。EXTRACT-MAX(S):去掉并返回\(S\)中具有最大关键字的元素。INCREASE-KEY(S, x, k):将元素\(x\)的关键字值增加到\(k\),这里假设\(k\)的值不小于\(x\)的原关键字值。
最大优先队列的一个应用:基于优先级的共享计算机系统的作业调度。最大优先队列记录将要执行的作业以及他们的优先级。当一个作业完成或者被中断后,调度器调用EXTRACT-MAX(S)从优先队列中选出最高优先级的作业执行。此外,还可以调用INSERT(S, x)把一个新作业加入到队列中。
最小优先队列支持的操作如下:
INSERT(S, x):把元素\(x\)插入集合\(S\)中。MINIMUM(S):返回\(S\)中具有最小关键字的元素。EXTRACT-MIN(S):去掉并返回\(S\)中具有最小关键字的元素。DECREASE-KEY(S, x, k):将元素\(x\)的关键字值减小到\(k\),这里假设\(k\)的值不大于\(x\)的原关键字值。
最小优先队列的一个应用:基于事件驱动的模拟器。发生时间作为关键字,事件必须按照发生的时间顺序进行模拟。
下面是最大优先队列的实现:
MAX-HEAP-MAXIMUM(A)
if A.heap-size < 1
error "heap underflow"
return A[1]
MAX-HEAP-EXTRACT-MAX(A)
max = MAX-HEAP-MAXIMUM(A)
A[1] = A[A.heap-size]
A.heap-size = A.heap-size - 1
MAX-HEAPIFY(A, 1)
return max
MAX-HEAP-INCREASE-KEY(A, x, k)
if k < x.key
error "new key is smaller than current key"
x.key = k
find the index i in array A where object x occurs
while i > 1 and A[PARENT(i)].key < A[i].key
exchange A[i] with A[PARENT(i)], updating the information that maps priority queue objects to array indices
i = PARENT(i)
MAX-HEAP-INSERT(A, x, n)
if A.heap-size == n
error "heap overflow"
A.heap-size = A.heap-size + 1
k = x.key
x.key = -∞
A[A.heap-size] = x
map x to index heap-size in the array
MAX-HEAP-INCREASE-KEY(A, x, k)
下面是MAX-HEAP-INCREASE-KEY的操作过程
在一个包含\(n\)个元素的堆中,所有优先队列的操作都可以在\(\Omicron(\log n)\)时间内完成。