4.3.1 有源RC滤波器
除了Gm-C滤波器外,另一种实现模拟集成滤波器的方案是有源RC滤波器或者MOSFET-C滤波器。在这两个技术中,电流的积分都是通过反馈连接在一个高增益放大器的电容上实现的,这与将电流积分电容连接到地的Gm-C滤波器方案不同。有时这种方案被叫做米勒积分,因为就像两级放大器中的米勒补偿电容,积分电容围绕高增益放大器连接。米勒积分提高了线性度,但是需要一个高增益带宽积的放大器,使得有源RC滤波器和MOSFET-C滤波器相比Gm-C滤波器一般更慢。同时,在CMOS工艺下它们的速度会更慢,因为放大器需要能驱动阻性负载,而Gm-C滤波器中只需要驱动容性负载。但在BiCMOS工艺下它们还是很有吸引力的,因为可以实现高跨导放大器。
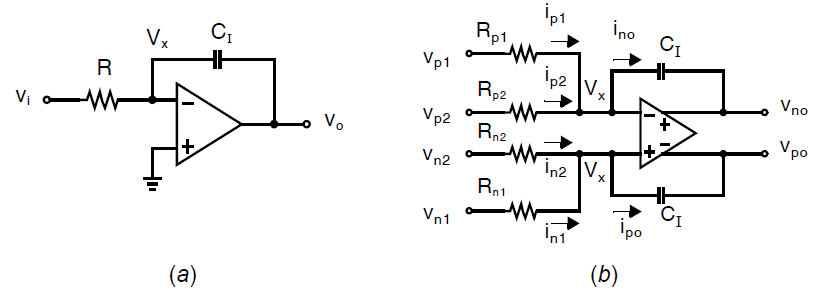
有源RC滤波器在分立器件和模拟集成电路滤波器中都很经典。考虑到模拟滤波器的主要组成单元是积分器,求和器以及增益级。一个基本的单端形式的有源RC积分器如下图(a)所示。假设放大器理想,虚地点在\(V_x\)。因此电压到电流通过电阻\(R\)来转换,转换的增益取决于电阻的阻值,但不幸的是,这个阻值是会随着工艺和温度差异而变化的。但是,使用一个被动电阻提供了绝佳的线性度。结果电流在电容\(C_I\)上积分并产生一个反相的输出\(v_o\)。
而在下图(b)中,积分器引入了求和。使用全差分放大器,电阻\(R_{p1,p2,n1,n2}\)将差分电压转换为差分电流。电流\(i_{p1,p2}\)和\(i_{n1,n2}\)在虚地节点\(V_x\)求和,使得总电流在电容\(C_I\)上积分。如果只需要增益和/或者求和,不需要积分的话,那么将围绕放大器的反馈电容换为电阻即可。
例题:
考虑如上图(a)中的有源RC积分器,假定放大器有着一阶开环响应,直流增益为\(A_0\),单位增益频率\(\omega_{ta}\),求积分器的频率响应。
解答:
闭环频率响应为理想频率响应\(-1/(sRC)\)乘以\(L(s)/(1+L(s))\),其中\(L(s)\)是整个电路的开环响应。
根据给定参数,可以写出放大器的开环响应为:
反馈网络的频率响应为:
由于\(L(s)=A(s)\beta(s)\)因此我们可以求出放大器的闭环频率响应为:
假定\(\omega_{ta}>>1/RC\),上式可以简化为:
这里额外说一下上面那个结论是怎么来的。假设有下图所示的反馈环路:
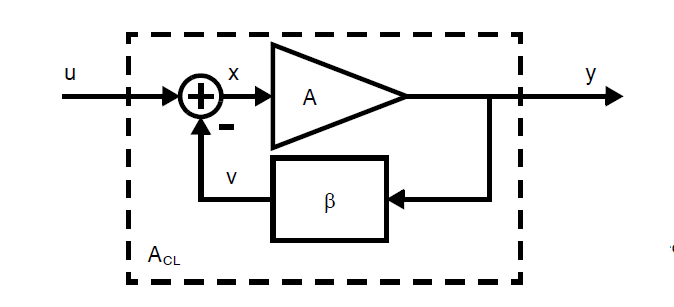
我们可以很简单的推出闭环响应\(A_{CL}\)为:
我们令\(L=A\beta\),即开环增益,那么:
当放大器理想,增益无穷大时\(L=\infin\),此时\(A_{CL}=1/\beta\)。
所以我们计算放大器不理想时的闭环增益,首先假设放大器理想,求出\(1/\beta\),再乘以修正项\(L/(1+L)\)即可,对于负反馈,可以在放大器负极断开环路,开环增益\(L(s)\)通过放大器频率响应\(A(s)\)和反馈网络频率响应\(\beta(s)=V_{FB}(s)/V_{out}(s)\)相乘即可求得。
根据\((4.3.4)\)我们可以得到波特图如下:
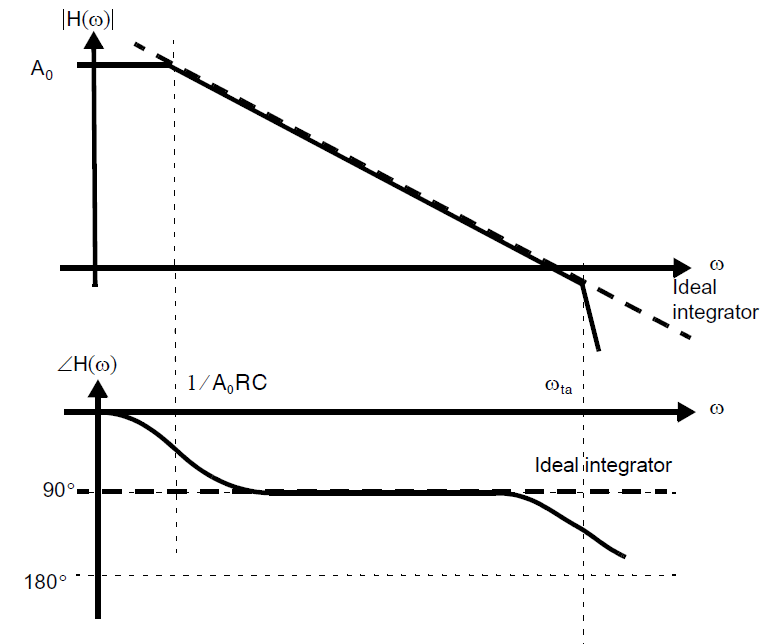
真实积分器响应对比理想积分器,第一点不同是直流增益仅为有限的\(A_0\)(而理想积分器是无穷大),对于高于\(1/A_0RC\)的角频率,真实频率响应很好的近似于理想频率响应\(-1/sRC\)。这之后,当频率接近放大器的单位增益频率时,积分器由于放大器有限的增益带宽而再次偏离理想值。因此积分器工作良好的频率区间为\(1/A_0RC<\omega < \omega_{ta}\),这对放大器的直流增益和单位增益频率提出了要求。
下图展示了一个使用两个有源RC积分器实现的二阶滤波器。
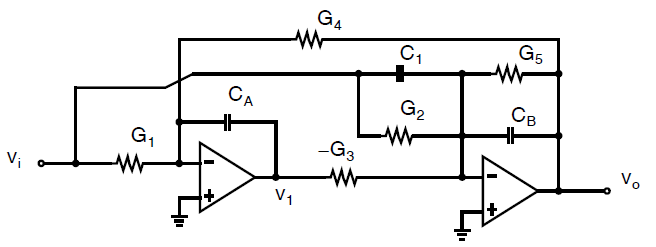
注意这个电路中需要两个放大器,每个积分器需要一个,因此每个都在滤波器中构成一个极点。第一个积分器的输出为:
第二个积分器的输出为:
结合两个公式整理后,我们可以得到:
显然这构成了一个二阶滤波器的系统传输函数。