题解
- AtCoder abc318_a Full Moon
- AtCoder abc318_b Overlapping sheets
- AtCoder abc318_c Blue Spring
- AtCoder abc318_d General Weighted Max Matching
- AtCoder abc318_e Sandwiches
- AtCoder abc318_f Octopus
- AtCoder abc318_g Typical Path Problem
- CodeForces 1861A Prime Deletion
- CodeForces 1861B Two Binary Strings
- CodeForces 1861C Queries for the Array
- CodeForces 1861D Sorting By Multiplication
AtCoder abc318_a Full Moon
高桥喜欢满月。
让今天成为第一天。今天或之后第一个能看到满月的日子是M天。之后,他每P天就能看到一次满月,即在M+P天、M+2P天,以此类推。
求出他能看到在第1天到第N天之间(包括第1天和第N天)的满月天数。
分析
要求 M+kP≤N 的情况下K的最大值
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f;
int main() {
int n, m, p;
while (cin >> n >> m >> p) {
cout << (n - m) / p + (n >= m);
}
return 0;
}
AtCoder abc318_b Overlapping sheets
在一个坐标平面上有N个矩形薄板。
每个薄片覆盖的矩形区域的每一侧都平行于x轴或y轴。
具体地说,第i张恰好覆盖了满足Ai≤x≤Bi和Ci≤y≤Di的区域。
设S是由一个或多个片材覆盖的区域的面积。可以证明,在约束条件下,S是一个整数。
打印一个整数S。
分析
标记思想,st[i][j]=1表示点(i,j) 被覆盖。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 110, INF = 0x3f3f3f3f;
int main() {
int n, a, b, c, d;
while (cin >> n) {
vector<vector<bool>> s(100, vector<bool>(100, 0));
for (int i = 1; i <= n; i++) {
cin >> a >> b >> c >> d;
for (int x = a; x < b; x++)
for (int y = c; y < d; y++) s[x][y] = 1;
}
int res = 0;
n = 100;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) res += s[i][j];
cout << res << endl;
}
return 0;
}
AtCoder abc318_c Blue Spring
Takahashi 正在计划一次为期N天的火车旅行。
对于每一天,他可以支付常规票价或使用一天通行证。
这里,对于1≤i≤N,行程第i天的常规票价为Fi日元。
另一方面,一批每份D张的一天通行证的售价为P日元。您可以购买任意数量的通行证,但只能以D为单位。
购买的每张通行证可以在任何一天使用,旅行结束时吃一些剩菜也没关系。
找到N日游的最低可能总成本,即购买一天通行证的成本加上一天通行证未涵盖天数的常规总票价。
分析
如果购买通行证的费用比常规票价便宜,那就购买通行证,所以可以先排序。
需要注意通行证是每d天作为一个单位购买。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 110, INF = 0x3f3f3f3f;
int main() {
int n, d, p;
while (cin >> n >> d >> p) {
vector<int> f(n);
for (int i = 0; i < n; i++) cin >> f[i];
sort(f.begin(), f.end(), greater<int>());
LL s = 0, res = 0;
for (int i = 0; i < n; i++) {
s += f[i];
if ((i + 1) % d == 0 || i == n - 1)
res += min(1ll * p, s), s = 0;
}
cout << res << endl;
}
return 0;
}
AtCoder abc318_d General Weighted Max Matching
给出了一个加权无向完全图,其中N个顶点编号从1到N。连接顶点 i 和 j (i<j) 的边的权重为\(D_{i,j}\)。
当在以下条件下选择一定数量的边时,找到所选边的最大可能总权重。
- 所选边的端点是两两不同。
分析
对于数据量20左右题目,可以考虑复杂度 \(2^n, n!\)的算法,如搜索剪枝,状压dp(二进制枚举)的算法,
-
搜索边:很直观的想法就是对于每条边,可以选也可以不选,共有 \(m=\sum_{i=1}^{n-1} i=120\),如果单纯枚举,有 \(2^{120}\) 种方案,会超时;考虑剪枝,但是无法证明剪枝后的效率可靠。
-
搜索点:因为点的数量较小,那么考虑搜索每个点选或不选,同时每个点连接 \(n-1\) 条边,复杂度 \(O(2^{n}✖n)\)
-
状态压缩dp:所谓状压dp就是用二进制来表示当前状态/或者说当前方案.
1) 状态定义:\(dp_[i]\) 表示当前方案为 i 时的最优解。
如:i=15(10)=1111(2) 表示已选择编号为 1,2,3,4的点。
2)状态转移:\(dp_{[k|s]} =max(dp_{[k|s]}, dp_{[k]}+w)\)
其中 s=(1<<i)|(1<<j) 表示选择的两个点,w 为连接这两个点的边的权值。
如果可以由状态s转移过来,那么之前一定没有选择这两个点,也就是 k&s=0。
比如:s=0000 1100(2),意味着当前选择的是编号为 3,4 的点;那么 k 一定不包含这两个点,也就是 k=xxxx 00xx,此时 k&s=0,证明可以从 s 转移到 k|s。
3)最终目标:每次选择两个点,那么最后目标就是所有选两个点(二进制有偶数个1)的状态的最大值,也可以在每次转移时维护答案。
4)复杂度分析: 任意两个点的组合情况为 \(C_n^2\) 种,所有的状态情况有 \(2^{n}-1\) 种,所以整体复杂度为 \(O(2^n✖n^2)\).
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 20;
int n, m, d[N][N];
struct T {
int u, v, w;
bool operator<(const T& t) const { return w > t.w; }
};
vector<T> g;
vector<bool> st(N);
vector<LL> sum(N);
LL res;
// ------------------------------------------------
void dfs(int x, LL s) {
res = max(res, s);
if (x >= g.size())
return;
// if (s + sum[g.size() - 1] - sum[x - 1] <= res)
// return; // 企图搞一个剪枝,最后剪废了
int u = g[x].u, v = g[x].v, w = g[x].w;
if (st[u] + st[v] == 0) {
st[u] = st[v] = 1, dfs(x + 1, s + w);
st[u] = st[v] = 0;
}
dfs(x + 1, s);
}
int solve1() {
while (cin >> n) {
g.clear(), st.clear(), sum.clear(), res = 0;
// g.push_back({0, 0, 0});
for (int i = 1, x; i <= n - 1; i++)
for (int j = i + 1; j <= n; j++) {
cin >> x;
g.push_back({i, j, x});
}
sort(g.begin(), g.end());
// for (int i = 1; i <= n; i++)
// sum[i] = sum[i - 1] + g[i].w;
dfs(0, 0);
cout << res << endl;
}
return 0;
}
// ------------------------------------------------
void dfs2(int x, LL s) {
res = max(res, s);
if (x > n)
return;
if (st[x]) {
dfs2(x + 1, s);
return;
}
for (int i = x + 1; i <= n; i++) {
if (!st[i]) {
st[x] = st[i] = 1, dfs2(x + 1, s + d[x][i]);
st[x] = st[i] = 0;
}
}
dfs2(x + 1, s);
}
int solve2() {
while (cin >> n) {
g.clear(), st.clear(), res = 0;
for (int i = 1, x; i <= n - 1; i++)
for (int j = i + 1; j <= n; j++) {
cin >> x;
d[i][j] = x;
}
dfs2(1, 0);
cout << res << endl;
}
return 0;
}
// ------------------------------------------------
int solve3() {
while (cin >> n) {
vector<LL> dp(1 << n);
res = 0;
for (int i = 0, x; i < n; i++)
for (int j = i + 1; j < n; j++) {
cin >> x;
int s = (1 << i) | (1 << j);
for (int k = 0; k < (1 << n); k++)
if (!(k & s)) {
dp[k | s] = max(dp[k | s], dp[k] + x);
res = max(res, dp[k | s]);
}
}
cout << res << endl;
}
return 0;
}
int main() {
// solve1();
// solve2();
solve3();
return 0;
}
AtCoder abc318_e Sandwiches
给出了一个长度为N: A=(A1,A2,...,AN)的正整数序列。
求满足以下条件的正整数 (i,j,k) 三元组数:
- 1≤i<j<k≤ N,Ai=Ak, Ai≠Aj.
分析
直接枚举i,j,k会TLE,当我们看数据的时候其实会发现,出现一个数据就可以确定该数据对答案的贡献,那么也就是说存在 \(O(n)\) 的解法--- 当然,这是一种感性的直觉。
- 如果 找到 Ai=Ak 的数量,以及 Ai=Aj=Ak 的数量,那么两者的差值就是答案。
1)Ai=Ak的数量可以通过模拟样例找到如下图的规律求得。
通过模拟样例,可以发现,每个元素的贡献.
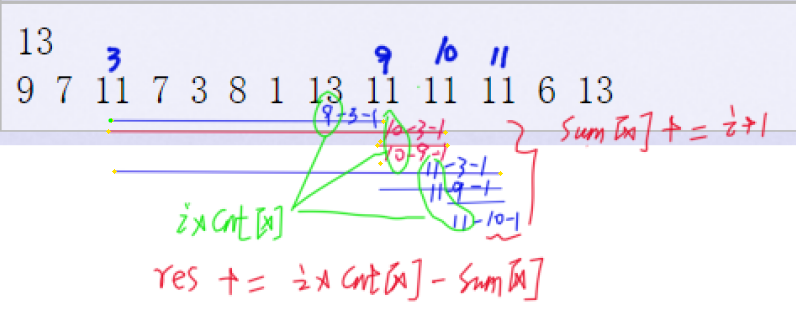
2)Ai=Aj=Ak 的数量可以通过组合数求的,即在 cnt[x] 个数中任选3个数进行组合 \(C_n^3\).
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 10, INF = 0x3f3f3f3f;
int T = 1, n;
int main() {
while (cin >> n) {
LL res = 0;
vector<LL> cnt(n + 1, 0), sum(n + 1, 0);
for (int i = 1, x; i <= n; i++) {
cin >> x;
res += i * cnt[x] - sum[x];
++cnt[x], sum[x] += i + 1;
}
for (int i = 1; i <= n; i++) {
LL m = cnt[i];
res -= m * (m - 1) * (m - 2) / 6;
}
cout << res << endl;
}
return 0;
}
AtCoder abc318_f Octopus
分析
点击查看代码
AtCoder abc318_g Typical Path Problem
分析
点击查看代码
CodeForces 1861A Prime Deletion
分析
点击查看代码
CodeForces 1861B Two Binary Strings
分析
点击查看代码
CodeForces 1861C Queries for the Array
分析
点击查看代码
CodeForces 1861D Sorting By Multiplication
分析
点击查看代码