526互联

Atcoder Xmas Contest 2022 H - Happy Game

发布时间 2024-01-07 19:35:31作者: Imcaigou

Atcoder Xmas Contest 2022 H - Happy Game

H - Happy Game (atcoder.jp)

没找到英文题解的一道题，或许很冷门。神秘。

Problem

给一张简单无向联通图，初始所有点都为白点。A 可以选择一个点，将其染黑；之后每次操作 B 可以选择最多两个在本次染色前相邻点存在黑点的点，将他们染成黑点。

A 想最大化 B 的操作数，B 想最小化自己的操作数。

问两方分别采取最优解时，B 的操作数（同时染两个点时，算一次操作）。

Solution

在下文中计数的所有相关概念中不包括初始点 \(u\) 。

如果 B 每次都可以染色两个点，那么答案就很好算了。但是有时候 B 只能染一个点，我们把这种情况称为“卡住了”，称在某个点卡住了则说明在这个情景下 B 下一步只能染这一个点。

假设 A 选择了 \(u\) 点。

会发现原问题相当于是求 B 在最优策略下会有多少次被卡住。

考虑到在 B 的最优策略这一条件下，那么卡住的情况一定不会发生在点双的内部，这是比较显然的，否则一定可以通过简单的调整使得其不会被卡住。

所以有：

Task 1. B 卡住的情况一定会发生在点双的边界上。

令 \(\mathrm{dis}(x,y)\) 表示原图上 \(x\) 与 \(y\) 的最小距离，\(\mathrm{C}(x,d)\) 表示距离 \(x\) 不超过 \(d\) 的点的个数（如上文所说，不包括 \(u\) 点）。

设第一次卡住卡在了 \(v\) 点，染完 \(v\) 后一共染过 \(d\) 次操作，应有 \(\mathrm{dis}(u,v) \le d\)。

实际上到现在我们已经染了 \(2d - 1\) 个点。

Task 2. 第一次被卡住的必要条件应该是 \(\mathrm{C}(u,\mathrm{dis}(u,v))=2d - 1\)。

由 Task 1 可知 \(v\) 应该是一个割点，所以想象中把 \(v\) 点删去后的包含 \(u\) 的连通块（即下文的“包含 \(u\) 的连通块”）大小 \(\ge \mathrm{C}(u,\mathrm{dis}(u,v))\)，又因为连通以及第一次卡住这些条件的限制可知：

如果 \(\mathrm{C}(u,\mathrm{dis}(u,v)) < 2d - 1\) 则显然 \(v\) 不可能是第一个被卡住的点，因为就算每次染两个点把这个包含 \(u\) 的连通块染满了也没有 \(d\) 次操作。

如果 \(\mathrm{C}(u,\mathrm{dis}(u,v)) > 2d - 1\) 则说明包含 \(u\) 的连通块中应该还有可以染的点，是所以 \(v\) 在最优策略下一定不会被第一个卡住。另外这里说一下，\(v\) 的被卡住一定不可能是主动的，即在有点可以染时故意不染，因为一定会更劣，考虑一下一般情况就知道了。

同样可知的是：

Task 3. 我们染 \(v\) 点以前包含 \(u\) 的连通块应该已经被染满了。

这启发我们依次被卡住的点 \(a_1,a_2,\cdots,a_k\) 应该在一条链上，且 \(\mathrm{dis}\) 应该越大越好，因为走的越远，中途可以用来防止被卡住的点就越多。

设 \(d_0\) 为最小的满足 \(c_{d_0}=2d_0-1\) 的值，则希望 \(\mathrm{dis}(u,v)= d_0\)，发现一定可以取等（这个比较好理解），否则可以不被卡住。其实也就相当于是从 \(u\) 到 \(v\) 的最短路径上的点参与了每一次染色，即每一次染色时总会有一个这条路径上的点被染黑。

所以我们由此得出了 B 的最优策略：

每次找到 \(\mathrm{dis}\) 最小的满足 \(\mathrm{C}(u,\mathrm{dis}(u,v))=2\mathrm{dis}(u,v) - 1\) 的 \(v\) ，显然 \(v\) 是唯一的，否则 \(\mathrm{dis}\) 一定不是最小的，那么可知 \(a_1=v\)；然后我们再找到这之后 \(\mathrm{dis}\) 最小的满足 \(\mathrm{C}(u,\mathrm{dis}(u,v'))=2\mathrm{dis}(u,v') - 2\) 的点（因为已经有一次操作只染了一个点），可知 \(a_2=v'\)，以此类推。

所以最后一次卡住的点 \(a_k\) 我们记为 \(a\)，则应该有 \(\mathrm{C}(u,\mathrm{dis}(u,a)) = 2\mathrm{dis}(u,a) - k\)。所以可知 \(k = 2\mathrm{dis}(u,a) - \mathrm{C}(u,\mathrm{dis}(u,a))\)。

答案应该是 \(\lceil \frac{n-1-k}{2} \rceil\)。

那么考虑如果有一个 \(a'\) 不为 \(a\)，一定是整个操作中有不合法行为的，即在该染一个点时染了两个点，或者没有考虑卡没卡住，所以答案会偏小。

所以再把 A 的最优策略考虑进来，我们求答案，相当于求 \(k_{\max}=\max_u\max_a\{2\mathrm{dis}(u,a) - \mathrm{C}(u,\mathrm{dis}(u,a))\}\)。

好耶 \(O(n^2)\) 暴力启动！

我们将外层的两个 \(\max\) 交换，显然求值不变。

那么相当于是对于 \(a\) 来找 \(u\)。考虑因为 \(a\) 一定是一个割点 （Task 1），所以 \(u\) 一定在割掉 \(a\) 所剩下的连通块当中。由 Task 3 可知，整个包含 \(u\) 的连通块应该都会被染满，所以我们就确定了 \(\mathrm{C}(u,\mathrm{dis}(u,a))=|S(u)|\)，其中 \(S(u)\) 表示包含 \(u\) 的连通块的大小。

所以我们相当于在 \(S(u)\) 中找到一个 \(\mathrm{dis}\) 最大的点就行了。

那么换一种思考方式，考虑存在一个 \(v\)，使得割去 \(a\) 后 \(u,v\) 不连通，\(v\) 可以等于 \(a\)。

那么我们可以在关于 \(v\) 的 bfs 树上遍历，找到 \(a\) 点为点双边界，那么关于 \(v,a\) 的最优的 \(u\) 应该是 bfs 树上 \(a\) 子树内最深的点。

那考虑是否可以找到常数级别个数的 \(v\) 使得可以找到最优的 \(a,u\) 呢？

答案是可以的。

Task 4. \(v \in \{p,q\}\)，其中 \(p,q\) 为原图的圆方树上直径的两个端点（一定是原图中的点）。

证明：

考虑反证，讨论不合法的情况。

这里的 \(\mathrm{dis}\) 均只考虑路径上的圆点。

第一种情况是，\(p,q\) 之间的路径与 \(u,a\) 之间的路径没有交，结合限制，应该长这样：

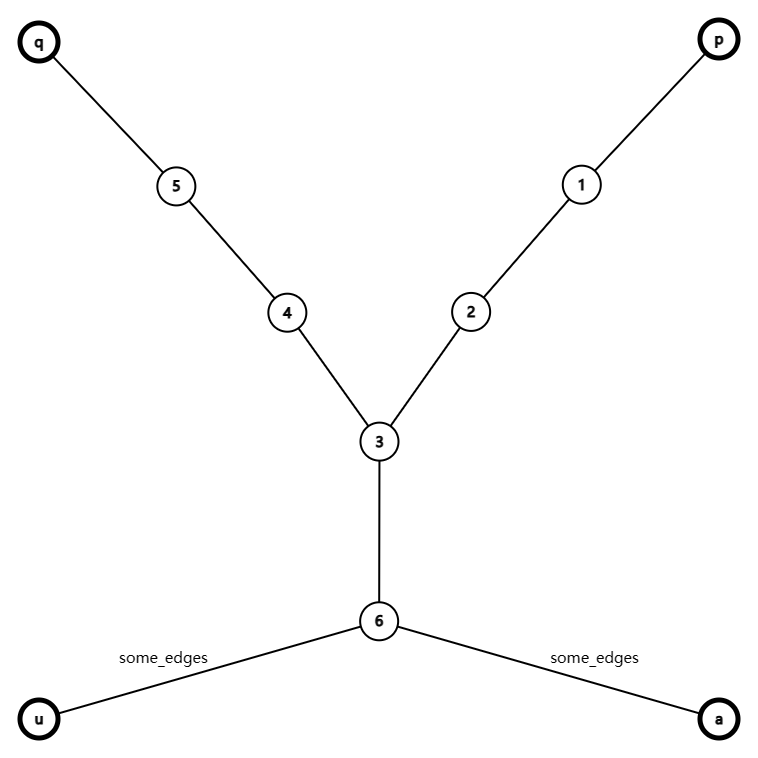
那么会发现因为 \(\mathrm{dis}(p,q) \ge \mathrm{dis}(u,a)\)，甚至从 \(u\) 染到 \(a\) 用的染色次数 \(d=\mathrm{dis}(u,a) \le \mathrm{dis}(p,q)\) ，所以可知 \(a\) 一定是不合法的而偏小，可以不计入答案。

第二种情况是，\(p,q\) 之间的路径与 \(u,a\) 之间的路径有交，结合限制，应该长这样：

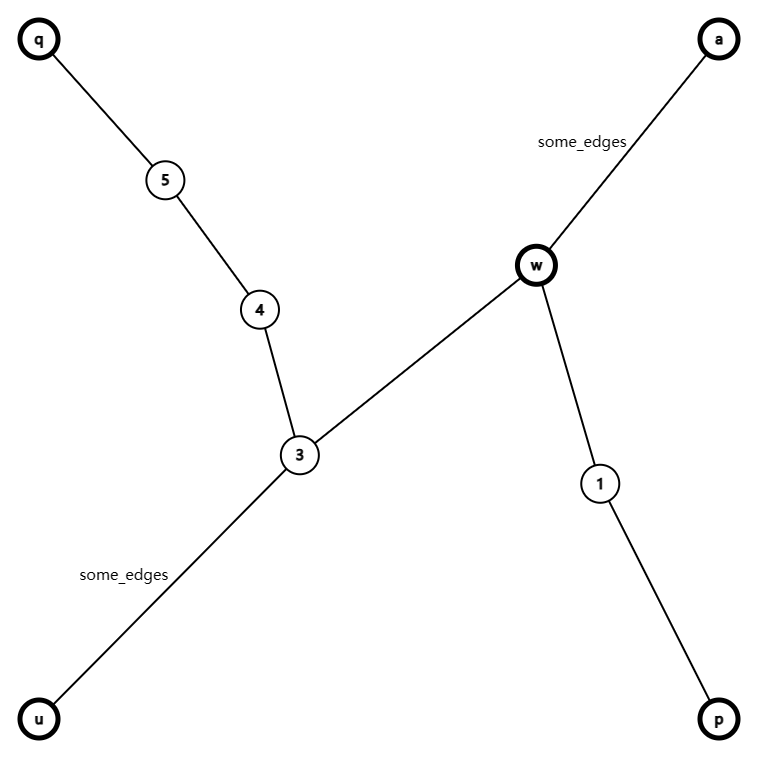
假设 \(w\) 是直径上最靠近 \(a\) 的点。那么会发现可以把 \(a\) 调整成 \(w\)，此时依据我们得出的 \(k=2\mathrm{dis(\cdots)}-\mathrm{C}(\cdots)\) 的结论，这次调整在 \(\mathrm{dis}\) 上的变化是 \(-\mathrm{dis}(w,a)\)，而在 \(\mathrm{C}\) 上的变化是 \(\ge \mathrm{dis}(w,p)\) 的（这个路径不会再被考虑进割去最优的 \(a\) 后 \(u\) 的连通块内了）。所以显然调整为 \(w\) 后贡献不劣。

即证。

所以只需要建出圆方树从两个端点各自求出最优解。

求的方法就是先 bfs 求出 \(\mathrm{dis}\)，然后再在割点上找子树内点的最远距离和子树大小，按结论求最大值就可以了。

Code

// atcoder xmas2022 h
#include <bits/stdc++.h>
using namespace std;
inline int read (){
    int p = 0;
    char c = getchar ();
    while (c < '0' && c > '9')
        c = getchar ();
    while (c >= '0' && c <= '9'){
        p = (p << 1) + (p << 3) + (c - 48);
        c = getchar ();
    }
    return p;
}
inline void write (int x){
    if (x > 9)
        write (x / 10);
    putchar (x % 10 + 48);
}
const int N = 6e5 + 5, M = 6e5 + 5;
int n, m;
int firs[N], nex[M << 1], to[M << 1], tot;
void Add (int u, int v){
    ++ tot;
    nex[tot] = firs[u];
    firs[u] = tot;
    to[tot] = v;
    ++ tot;
    nex[tot] = firs[v];
    firs[v] = tot;
    to[tot] = u;
}
int idx, dfn[N], low[N], sta[N], top;
int cnt_bcc;
vector < int > gto[N << 1];
void Tarjan (int u){
    dfn[u] = low[u] = ++ idx;
    sta[++ top] = u;
    for (int e = firs[u], v;e;e = nex[e]){
        v = to[e];
        if (! dfn[v]){
            Tarjan (v);
            low[u] = min (low[u], low[v]);
            if (low[v] == dfn[u]){
                ++ cnt_bcc;
                int p;
                do {
                    p = sta[top --];
                    gto[p].push_back (cnt_bcc);
                    gto[cnt_bcc].push_back (p);
                } while (p != v);
                gto[u].push_back (cnt_bcc);
                gto[cnt_bcc].push_back (u);
            }
        } else
            low[u] = min (low[u], dfn[v]);
    }
}
int s, t, dis[N << 1], maxdis[N], sz[N], ans;
void Find (int u, int father, int &tar){
    dis[u] = dis[father] + 1;
    for (int v : gto[u]){
        if (v == father)
            continue;
        Find (v, u, tar);
    }
    if (dis[tar] < dis[u])
        tar = u;
}
void Bfs (int _start){
    for (int i = 1;i <= n;++ i)
        dis[i] = 0x3f3f3f3f;
    queue < int > Q;
    Q.push (_start);
    dis[_start] = 0;
    while (! Q.empty ()){
        int u = Q.front ();
        Q.pop ();
        for (int e = firs[u], v;e;e = nex[e]){
            v = to[e];
            if (dis[v] > dis[u] + 1){
                dis[v] = dis[u] + 1;
                Q.push (v);
            }
        }
    }
}
void _Tarjan (int u){
    dfn[u] = low[u] = ++ idx;
    sz[u] = 1;
    maxdis[u] = dis[u];
    for (int e = firs[u], v;e;e = nex[e]){
        v = to[e];
        if (! dfn[v]){
            _Tarjan (v);
            sz[u] += sz[v];
            maxdis[u] = max (maxdis[u], maxdis[v]);
            low[u] = min (low[u], low[v]);
            if (low[v] >= dfn[u])
                ans = max (ans, ((maxdis[v] - dis[u]) << 1) - sz[v]);
        } else
            low[u] = min (low[u], dfn[v]);
    }
}
void Clear (){
    idx = ans = 0;
    for (int i = 1;i <= (n << 1);++ i)
        gto[i].clear (), firs[i] = dfn[i] = low[i] = dis[i] = 0;
}
void WORK (){
    n = read (), m = read ();
    Clear ();
    for (int i = 1, u, v;i <= m;++ i){
        u = read (), v = read ();
        Add (u, v);
    }
    cnt_bcc = n;
    Tarjan (1);
    s = t = 0;
    Find (1, 0, s);
    Find (s, 0, t);
    Bfs (s);
    for (int i = 1;i <= n;++ i)
        dfn[i] = low[i] = 0;
    idx = 0;
    _Tarjan (s);
    Bfs (t);
    for (int i = 1;i <= n;++ i)
        dfn[i] = low[i] = 0;
    idx = 0;
    _Tarjan (t);
    write ((n + ans) / 2), putchar ('\n');
    return ;
}
signed main (){
    int T = read ();
    while (T --)
        WORK ();
    return 0;
}