首先,严格地讲,基环树不是树,它是一张有 \(n\) 个节点、\(n\) 条边的图。
介绍
无向图上的基环树
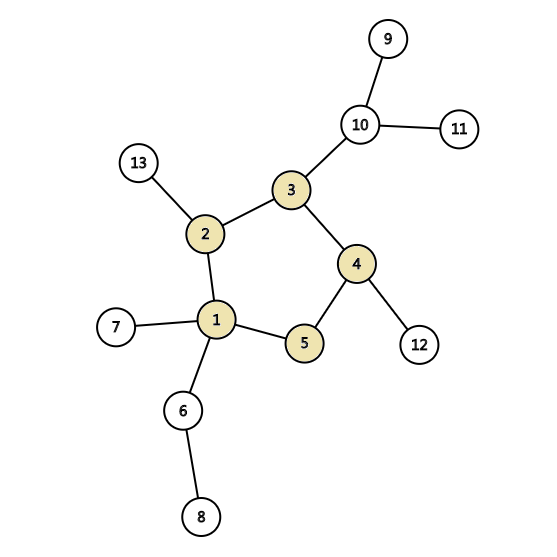
有向图上的基环树
内向树
出度为 1
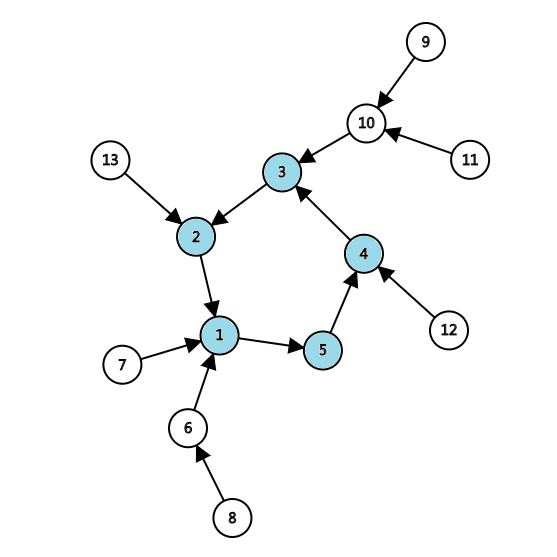
外向树
入度为 1
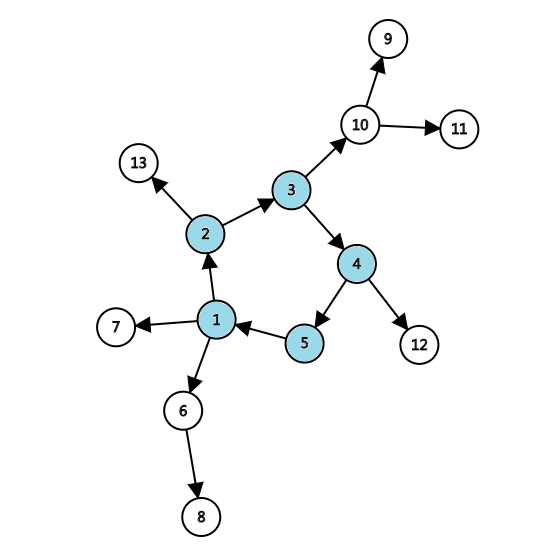
流程
- 找到唯一的环;
- 对环之外的部分按照若干棵树处理;
- 考虑与环一起计算。
找环
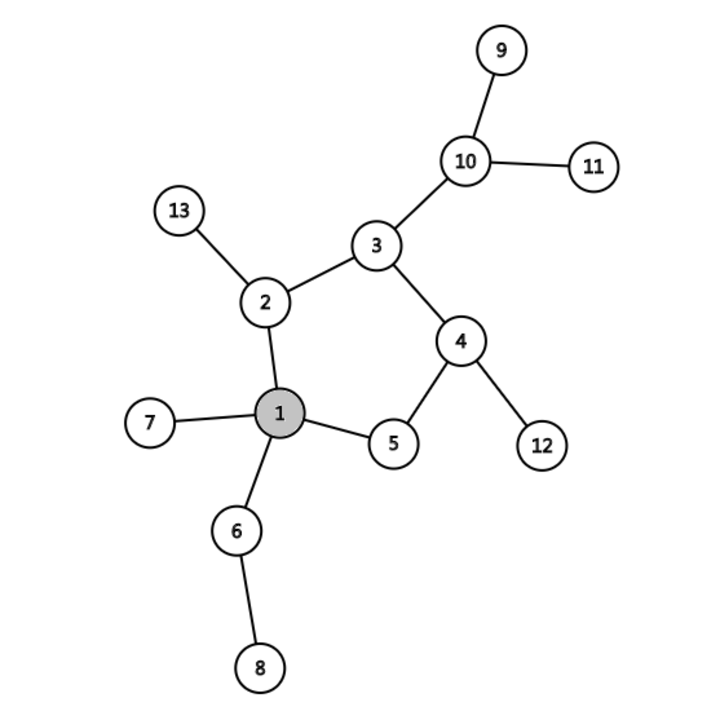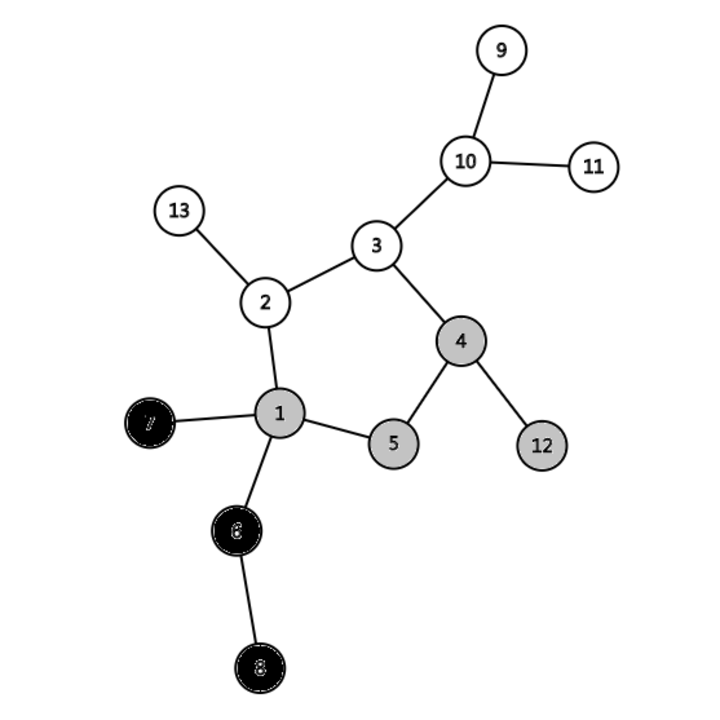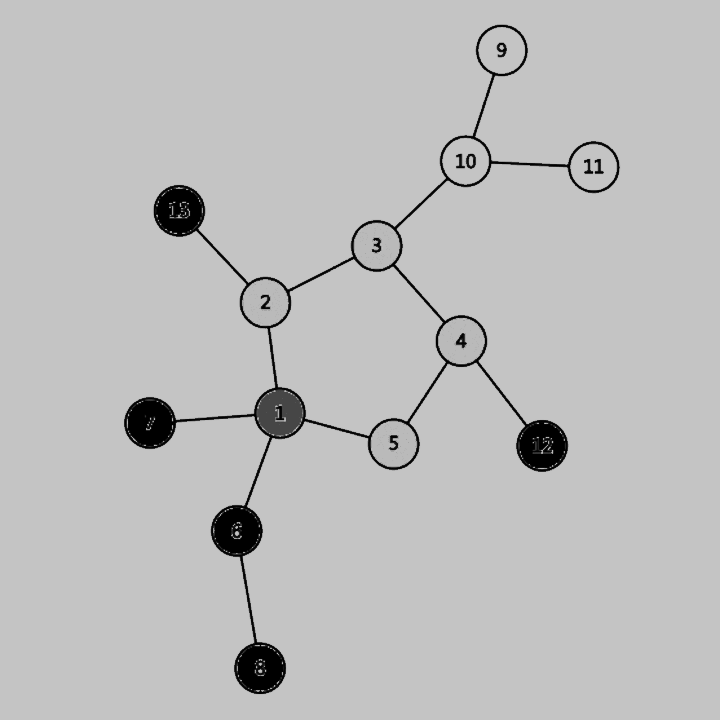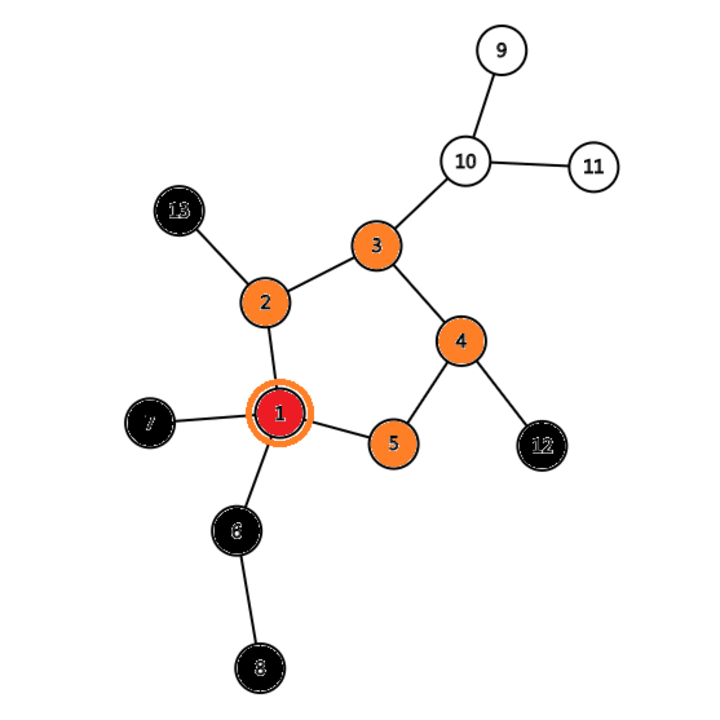
- 从任意一点开始搜索;
- 每次拓展到的点涂为灰色,回溯的点涂为黑色;
- 重复第一、二步,直到通过一条未经过过的边拓展到一个灰色节点;
- 将拓展到的灰色节点涂为红色,函数返回 true;
- 将经过的回溯时经过的节点涂为橙色,函数返回 true;
- 重复第 5 步,直到回溯到被涂为红色的节点,函数返回 false,算法结束。
bool get_ring(int x, int ff){
if (v[x] == 1){
v[x] = 2, v2[x] = 1, rin[++ tot] = x;
return true;
}
v[x] = 1; int opt = 0;
for (int i = hd[x]; i;i = e[i].nxt){
if(v_e[i]) continue; v_e[i] = v_e[i ^ 1] = true;
int y = e[i].to;
if(get_ring(y, x)){
pre_e[y] = i;
if (v[x] != 2){
rin[++ tot] = x, v2[x] = 1;
return true;
}
else return false;
}
}
return false;
}
对于基环树森林,我们可以用如下几种方法来操作:
- 在环上节点递归前,用另一个 dfs 遍历该节点能到达的所有节点,并标记。
- 在对去掉环之后的若干棵子树进行处理时进行另一种标记 v2[],判断是否是一棵新的基环树的依据为 v2[] 是否被标记。
- 建图时使用并查集。
找环之后的操作就要视题目而定了,不过一般是一个树形DP(子树不考虑环)加一个线性DP+单调队列优化(在环上,断环为链,复制一遍)
例题
Ⅰ. P2607 [ZJOI2008] 骑士
对于环上的每条边,将它断掉,成为一棵树后,直接 没有上司的舞会 DP, 注意有两种情况,不选 \(u1\) 和不选 \(u2\)。
#include<bits/stdc++.h>
#define N 1000005
#define LL long long
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
int x1,tot,n;
int Head[N],to[N<<1],Next[N<<1],val[N],a[N];
bool vis[N];
LL f[N][2],ans;
void add(int u,int v){to[++tot]=v,Next[tot]=Head[u],Head[u]=tot;}
void dfs(int x){
vis[x]=1,f[x][0]=0,f[x][1]=val[x];
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(y==x1) continue;
dfs(y);
f[x][1]+=f[y][0];
f[x][0]+=max(f[y][1],f[y][0]);
}
}
signed main(){
n=read();
for(int i=1;i<=n;i++){
val[i]=read();
int v=read();add(v,i),a[i]=v;
}
for(int i=1;i<=n;i++){
if(vis[i]) continue;
x1=i;
while(!vis[a[x1]]){vis[x1]=1,x1=a[x1];}
dfs(x1);
LL res=f[x1][0];
x1=a[x1];
dfs(x1);
res=max(res,f[x1][0]);
ans+=res;
}
printf("%lld\n",ans);
return 0;
}
Ⅱ. P1399 [NOI2013] 快餐店
由于这整张图是一个基环树,我们可以考虑每次破掉环上的一条边使它变成一颗树,然后求出直径,最后统计所有的直径中最短的那个作为答案即可。
- 这个直径完全在环上某一点所在的子树中。
- 这个直径从环上某一点所在子树出发,到达该点后在环上走过一些边到达另一个点,进入该点所在子树并且结束。
第一种情况直接统计环上点的子树即可。
第二种情况我们引入一些数组。
树的最大深度。所以我们预先处理环上所有点所在子树的最大深度记为dis_i。
然后我们定义四个数组,\(A,B,C,D\)。记环上点数为\(rcnt\),环上点离1号点的距离为\(pre_i\),离\(rcnt\)号点的距离为\(sub_i\)则
\(A_i\)表示环上\(1\leq x\leq i\)时\(dis_x+pre_x\)的最大值
\(B_i\)表示环上\(1\leq x\leq y\leq i\)中\(dis_x+dis_y-pre_x+pre_y\)的最大值
\(C_i\)表示环上\(i\leq x\leq rcnt\)中\(dis_x+sub_x\)的最大值
\(D_i\)表示环上\(i\leq x\leq y\leq rcnt\)中\(dis_x+dis_y+sub_x-sub_y\)的最大值
我们可以将 环上的点 \(i\) 与 \(i + 1\) 断开,此时的直径为 \(max(A_i + C_{i+1} + tmp, B_i, D_{i+1})\)
\(tmp\) 为 \(1\) 到 \(rcnt\) 的点之间的距离。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 4e5 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
bool _u;
int n, tot = 1, rcnt;
int hd[N], v[N], v2[N], rdis[N], rin[N];
bool v_e[N << 1];
ll ans;
ll A[N], B[N], C[N], D[N], dis[N];
// A 前缀 + 子树最大深度
// B 前缀中两个子树的最大深度 + 两点距离
// C 后缀 + 子树最大深度
// D 后缀中两个子树的最大深度 + 两点距离
struct Edge{
int to, nxt, w;
void add(int u, int v, int ww){
to = v, nxt = hd[u], hd[u] = tot, w = ww;
}
}e[N << 1];
bool get_ring(int x){
if (v[x] == 1){
v[x] = 2, v2[x] = 1, rin[++ rcnt] = x;
return true;
}
v[x] = 1; int opt = 0;
for (int i = hd[x]; i;i = e[i].nxt){
if(v_e[i]) continue; v_e[i] = v_e[i ^ 1] = true;
int y = e[i].to;
if(get_ring(y)){
if (v[x] != 2){
rdis[rcnt] = e[i].w;
rin[++ rcnt] = x, v2[x] = 1, v[x] = 2;
return true;
}
else return rdis[rcnt] = e[i].w, false;
}
}
return false;
}
void dfs(int x, int fa){
for(int i = hd[x]; i; i = e[i].nxt){
int y = e[i].to; if(y == fa || v[y] == 2) continue;
dfs(y, x);
ans = max(ans, dis[x] + dis[y] + e[i].w); //子树内直径
dis[x] = max(dis[x], dis[y] + e[i].w);
}
}
bool _v;
int main(){
cerr << abs(&_u - &_v) / 1048576.0 << "MB\n";
n = read();
for(int i = 1; i <= n; ++i){
int u = read(), v = read(), w = read();
e[++tot].add(u, v, w), e[++tot].add(v, u, w);
}
get_ring(1);
for(int i = 1; i <= rcnt; ++i) dfs(rin[i], 0);
ll sum = 0, maxn = 0;
for(int i = 1; i <= rcnt; ++i){
sum += rdis[i - 1];
A[i] = max(A[i - 1], dis[rin[i]] + sum);
B[i] = max(B[i - 1], sum + maxn + dis[rin[i]]);
maxn = max(dis[rin[i]] - sum, maxn);
}
sum = maxn = 0;
int tmp = rdis[rcnt]; rdis[rcnt] = 0;
for(int i = rcnt; i; --i){
sum += rdis[i];
C[i] = max(C[i + 1], dis[rin[i]] + sum);
D[i] = max(D[i + 1], sum + maxn + dis[rin[i]]);
maxn = max(dis[rin[i]] - sum, maxn);
}
ll ans2 = B[rcnt];
for(int i = 1; i < rcnt; ++i)
ans2 = min(max(max(B[i], D[i + 1]), A[i] + C[i + 1] + tmp), ans2);
printf("%lld\n", max(ans, ans2));
return 0;
}
Ⅲ.AT_arc079_d [ARC079F] Namori Grundy
题意:有一个弱联通的有向图,含有 \(n\) 个结点和\(n\)条边。试问是否存在方案,赋给每个结点一个自然数权值\(val_i\),满足对于所有结点\(u, val_u=mex\{val_v|(u,v)\in E\}\)。一个集合的\(mex\)是没有在这个集合中出现的最小自然数。
对于树上的点,显然可以直接做,对于环上的,分类讨论:
\((u,v)\) 为环上的一条边。
- \(val_u = val_v\), \(val_u = val_u + 1\)。
- \(val_u \notequal val_v\), 可以不操作。
发现无解的情况只有环上的 \(val\) 均相等,且环的个数为奇数。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
bool _u;
int n, tot, cnt;
int fa[N], hd[N], jud[N], val[N];
bool vis[N], cir[N];
struct Edge{
int to, nxt;
}e[N << 1];
void add(int u, int v){e[++tot].to = v, e[tot].nxt = hd[u], hd[u] = tot;}
void dfs(int x){
for(int i = hd[x]; i; i = e[i].nxt){
int y = e[i].to; if(!cir[y]) dfs(y);
}
for(int i = hd[x]; i; i = e[i].nxt){
int y = e[i].to; if(!cir[y]) jud[val[y]] = 1;
}
for(; jud[val[x]]; ++val[x]) ;
for(int i = hd[x]; i; i = e[i].nxt){
int y = e[i].to; if(!cir[y]) jud[val[y]] = 0;
}
}
bool _v;
int main(){
cerr << abs(&_u - &_v) / 1048576.0 << "MB\n";
n = read();
for(int i = 1; i <= n; ++i) fa[i] = read(), add(fa[i], i);
int p = 1;
for(; !vis[p]; p = fa[p]) vis[p] = 1;
for(; !cir[p]; p = fa[p]) cir[p] = 1;
int maxn = -1, minn = 1e9;
for(int i = 1; i <= n; ++i)
if(cir[i]){
++cnt; dfs(i);
maxn = max(maxn, val[i]), minn = min(minn, val[i]);
}
if(minn == maxn && cnt & 1) printf("IMPOSSIBLE\n");
else printf("POSSIBLE\n");
return 0;
}