526互联

Codeforces Round 892 (Div. 2)E. Maximum Monogonosity（动态规划，数学）

发布时间 2023-08-28 12:26:40作者: XiCen

题目链接：https://codeforces.com/contest/1859/problem/E

 

题意：

 

有长度为n的a和b俩个序列，定义f【l，r】 = abs（a【l】-b【r】） + abs（b【l】-a【r】）；

 

给正整数k，求  不相交 的 区间 且   所有   区间的长度  的  和  为 k 的 最大值  是多少？

 

分析：

 

这里借鉴一个佬的思路：

 

首先考虑比较正常的dp，dp【i】【j】 为前 i 的长度里 有 j 个 长度被选中的最大价值，那么转移方程是：

 

 

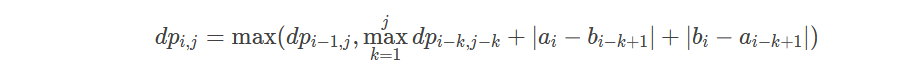
直接转移的话，时间复杂度是 O（n*k^2） ，显然是过不了，考虑优化；

 

看出原式是有绝对值的，考虑把绝对值展开：

 

 

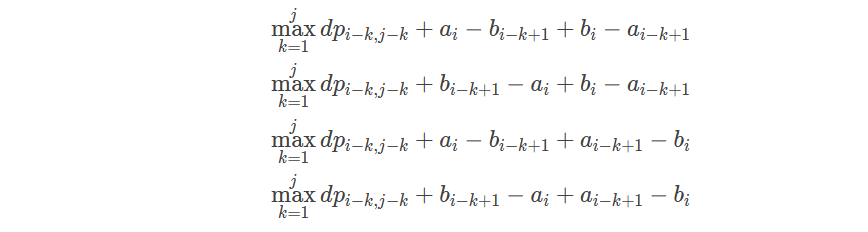
归纳总结一下：

 

 

 

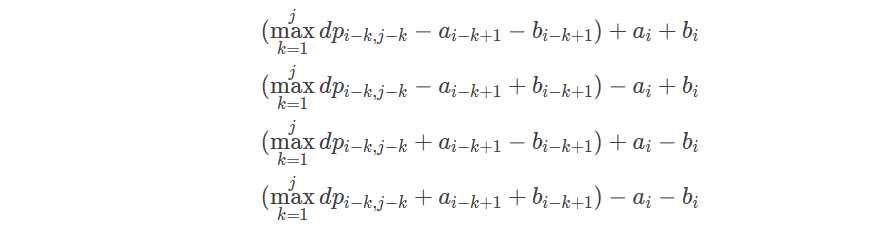
那么可以看出，我们可以用4个一维dp来记录一下左边括号内的数，那么时间复杂度可以优化到 ：O（n*k）；

 

代码：

 

#include<bits/stdc++.h>

#define int long long

const int N = 3e3 + 3;

int dp[N][N], f[4][N];

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    int T;
    std::cin >> T;
    while (T--) {
        int n, m;
        std::cin >> n >> m;
        std::memset(f, 0x80, sizeof f);
        std::vector<int> a(n + 1, 0), b(n + 1, 0);
        for (int i = 1; i <= n; ++i)std::cin >> a[i];
        for (int i = 1; i <= n; ++i)std::cin >> b[i];
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= m && j <= i; ++j) {
                dp[i][j] = dp[i - 1][j];
                f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);
                f[1][i - j] = std::max(f[1][i - j], dp[i - 1][j - 1] + a[i] - b[i]);
                f[2][i - j] = std::max(f[2][i - j], dp[i - 1][j - 1] - a[i] + b[i]);
                f[3][i - j] = std::max(f[3][i - j], dp[i - 1][j - 1] + a[i] + b[i]);
                dp[i][j] = std::max(dp[i][j], f[0][i - j] + a[i] + b[i]);
                dp[i][j] = std::max(dp[i][j], f[1][i - j] + a[i] - b[i]);
                dp[i][j] = std::max(dp[i][j], f[2][i - j] - a[i] + b[i]);
                dp[i][j] = std::max(dp[i][j], f[3][i - j] - a[i] - b[i]);
            }

        std::cout << dp[n][m] << "\n";
    }

    return 0;
}

感觉这题纯dp，先有朴素想法，然后把绝对值展开，再来个简单dp，结合一下就可以了：）