Preface
补题
这场补题的时候直接成腐乳了,A题挂两发,B题挂两发,C题挂一发是真的抽象
虽然D是个套路题看一眼就秒了,但如果真的比赛时候打真要罚时爆炸了的说
后面的EF还是做不来啊岂可修,不过都很有启发性让人感觉神清气爽,不像傻逼蓝桥杯花钱买罪受
A. Blackboard List
刚开始想错方向了,签到题写挂真没理由的
首先考虑求出\(a_i\)的最小值\(mi\),显然如果\(mi<0\)则它一定是初始的某个数之一,因为不可能生成负数
否则求出\(a_i\)的最大值\(mx\),则\(mx\)此时一定是初始的某个数之一,因为此时所有数都大于等于\(0\),那么其差的绝对值只会越来越小
#include<cstdio>
#include<iostream>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=105;
int t,n,x,mi,mx;
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d",&n),mi=1e9,mx=-1e9,i=1;i<=n;++i)
scanf("%d",&x),mi=min(mi,x),mx=max(mx,x);
printf("%d\n",mi<0?mi:mx);
}
return 0;
}
B. Minimize Permutation Subarrays
这题感觉比A题要简单点的说,不过我还是写挂了
其实很简单,只要把\(n\)插到\(1,2\)的中间即可保证没有除了\(\{1\}\)和整个序列之外的其它排列了
#include<cstdio>
#include<iostream>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005;
int t,n,a[N],pos[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d",&n),i=1;i<=n;++i) scanf("%d",&a[i]),pos[a[i]]=i;
int x=min(pos[1],pos[2]),y=max(pos[1],pos[2]);
if (pos[n]<x) printf("%d %d\n",pos[n],x); else
if (pos[n]>y) printf("%d %d\n",pos[n],y); else puts("1 1");
}
return 0;
}
C. No Prime Differences
一般Div2的构造还是很trivial的,刚开始想复杂了还好后面悬崖勒马
首先如果\(m\)不是质数的话就有个很trivial的构造方案,即形如这样的填法(\(n=4,m=4\)):
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
此时所有相邻数的差都是\(1\)或者\(m\),显然符合要求
否则此时\(m\)为质数,考虑\(m+1\)一定是合数,因此我们可以如下构造(\(n=5,m=5\)):
1 2 3 4 5
7 8 9 10 6
13 14 15 11 12
19 20 16 17 18
25 21 22 23 24
即如果我们把每行最小的数每次向右有一个\(m-1\)的循环移位,确定下它的位置之后按顺序填入其它数即可
代码就非常好写了
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=1005;
int t,n,m,a[N][N]; bool ispri[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i,j; for (i=2;i<=1000;++i) for (ispri[i]=1,j=2;j*j<=i;++j) if (i%j==0) ispri[i]=0;
for (scanf("%d",&t);t;--t)
{
if (scanf("%d%d",&n,&m),!ispri[m])
{
for (i=1;i<=n;++i) for (j=1;j<=m;++j) a[i][j]=(i-1)*m+j;
} else
{
for (i=1;i<=m;++i) a[1][i]=i; int dlt=m-1,pos=1,num=m;
for (i=2;i<=n;++i)
{
pos+=dlt; if (pos>m) pos-=m;
for (j=pos;j<=m;++j) a[i][j]=++num;
for (j=1;j<pos;++j) a[i][j]=++num;
}
}
for (i=1;i<=n;++i) for (j=1;j<=m;++j) printf("%d%c",a[i][j]," \n"[j==m]);
}
return 0;
}
D. Bracket Walk
经典套路题,感觉最近括号序列相关的题见的有点太多了,所以思路就很容易了
首先当整个序列长度为奇数时一定无解,因为不管怎么刷括号也不会改变两个括号差值的奇偶性
否则考虑套路地把左括号看成\(1\),右括号看成\(-1\),考虑什么时候我们需要刷左括号
很显然就是当存在某个位置的前缀和\(<0\)时就会有不合法的情况,我们把最左边的这个位置记为\(pos\)
那么我们现在要判断的就是在\(pos\)之前有没有连续两个左括号的出现,如果有的话我们直接在这里刷够左括号的数目使得后面不会出现前缀和\(<0\)的情形
对于右括号的讨论也是同理,我们也可以用经典套路,把整个括号序列reverse之后并把所有括号取反,就把刷右括号转化成和刷左括号一样的操作了
(不然的话要写两种线段树上二分代码量有点大的说)
然后维护这些信息显然直接用线段树维护前缀和序列的值即可,查询第一个小于\(0\)的位置只要维护区间最小值然后线段树上二分即可
至于那个连续的左括号的位置直接用set存一下即可,每次拿出其中最左的位置和\(pos\)比较一下即可
#include<cstdio>
#include<iostream>
#include<set>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005;
int n,q,x,a[N],b[N],pfx_a[N],pfx_b[N]; char s[N]; set <int> sa,sb;
class Segment_Tree
{
private:
struct segment
{
int mi,tag;
}node[N<<2];
#define MI(x) node[x].mi
#define T(x) node[x].tag
#define TN CI now=1,CI l=1,CI r=n
#define LS now<<1,l,mid
#define RS now<<1|1,mid+1,r
inline void pushup(CI now)
{
MI(now)=min(MI(now<<1),MI(now<<1|1));
}
inline void apply(CI now,CI mv)
{
MI(now)+=mv; T(now)+=mv;
}
inline void pushdown(CI now)
{
if (T(now)) apply(now<<1,T(now)),apply(now<<1|1,T(now)),T(now)=0;
}
public:
inline void build(int *pfx,TN)
{
T(now)=0; if (l==r) return (void)(MI(now)=pfx[l]);
int mid=l+r>>1; build(pfx,LS); build(pfx,RS); pushup(now);
}
inline void modify(CI beg,CI end,CI mv,TN)
{
if (beg<=l&&r<=end) return apply(now,mv); int mid=l+r>>1; pushdown(now);
if (beg<=mid) modify(beg,end,mv,LS); if (end>mid) modify(beg,end,mv,RS); pushup(now);
}
inline int query(TN)
{
if (MI(now)>=0) return n+1; if (l==r) return l; int mid=l+r>>1; pushdown(now);
if (MI(now<<1)<0) return query(LS); return query(RS);
}
#undef M
#undef T
#undef TN
#undef LS
#undef RS
}A,B;
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d%d%s",&n,&q,s+1),i=1;i<=n;++i)
a[i]=s[i]=='('?1:-1,b[n-i+1]=-a[i];
for (sa.clear(),sb.clear(),i=1;i<n;++i)
{
if (a[i]==1&&a[i+1]==1) sa.insert(i);
if (b[i]==1&&b[i+1]==1) sb.insert(i);
}
for (i=1;i<=n;++i) pfx_a[i]=pfx_a[i-1]+a[i],pfx_b[i]=pfx_b[i-1]+b[i];
for (A.build(pfx_a),B.build(pfx_b),i=1;i<=q;++i)
{
if (n&1) { puts("NO"); continue; }
scanf("%d",&x); A.modify(x,n,-2*a[x]); B.modify(n-x+1,n,-2*b[n-x+1]);
if (x<n&&a[x]==1&&a[x+1]==1) sa.erase(x);
if (x>1&&a[x-1]==1&&a[x]==1) sa.erase(x-1);
a[x]*=-1; if (x<n&&a[x]==1&&a[x+1]==1) sa.insert(x);
if (x>1&&a[x-1]==1&&a[x]==1) sa.insert(x-1);
x=n-x+1; if (x<n&&b[x]==1&&b[x+1]==1) sb.erase(x);
if (x>1&&b[x-1]==1&&b[x]==1) sb.erase(x-1);
b[x]*=-1; if (x<n&&b[x]==1&&b[x+1]==1) sb.insert(x);
if (x>1&&b[x-1]==1&&b[x]==1) sb.insert(x-1);
int pa1=sa.empty()?n+1:*sa.begin(),pa2=A.query();
int pb1=sb.empty()?n+1:*sb.begin(),pb2=B.query();
if (pa1<=pa2&&pb1<=pb2) puts("YES"); else puts("NO");
}
return 0;
}
E. Count Supersequences
龟龟原来答案和序列的形态无关,真是太巧妙了的说
首先我们可以尝试先写个暴力DP,设\(f_{i,j}\)表示填了序列\(b\)的前\(i\)位,匹配序列\(a\)的最长前缀的长度为\(j\)的方案数
转移的话考虑这一位填的是否和\(a\)中下一个位置匹配来转移,而且要注意如果\(j\)是\(a\)的最后一个位置(即之前以及全部匹配了)就可以随便填,因为前面的已经合法了
写成转移方程就是这样:
然后我们可以很惊喜地发现这个DP和\(a_i\)的具体形态无关,那么就意味着我们可以任意地修改\(a_i\)的取值来简化问题
比如此时我们可以令所有的\(a_i\)都为\(1\),此时题目转化为,求\(b\)的方案数使得序列中至少有\(n\)个\(1\)
考虑到\(m\)较大而\(n\)较小,因此可以容斥计算答案,即枚举不合法的只放了\(i\)个\(1\)的方案,则:
现在还有一个问题就是\(m\)很大时组合数\(C_m^i\)的值应该怎么快速计算,考虑因为要求的所有组合数的下标其实都一样,因此可以用递推求解:
因此总复杂度\(O(n\log m)\)
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005,mod=1e9+7;
int t,n,m,k,x,coef,ans;
inline void dec(int& x,CI y)
{
if ((x-=y)<0) x+=mod;
}
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d%d%d",&n,&m,&k),i=1;i<=n;++i) scanf("%d",&x);
for (ans=quick_pow(k,m),coef=1,i=0;i<n;++i)
dec(ans,1LL*coef*quick_pow(k-1,m-i)%mod),coef=1LL*coef*(m-i)%mod*quick_pow(i+1)%mod;
printf("%d\n",ans);
}
return 0;
}
F. Stuck Conveyor
妙题,其实前面有一个差不多的做法但感觉写起来很麻烦,看了Tutorial只能说是醍醐灌顶
本题最核心的思想就是构建两种蛇形的方案,即:
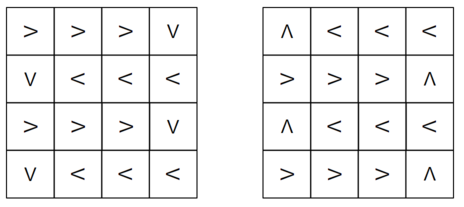
不难发现这两种方案都经过了所有格子各一次,并且第二种方案就是第一种方案路径的反向
考虑按照第一种方案的顺序给格子赋上\(1\sim n^2\)的编号,则第一种方案总是从编号小的走到编号大的,第二章方案则恰好相反
现在考虑我们分别以编号为\(1\)的格子为初始位置,并用方案一来询问得到一组反馈\(x_1,y_1\),同时以编号为\(n^2\)的格子为初始位置,并用方案二来询问得到一组反馈\(x_2,y_2\)
考虑现在如果\(x_1=x_2,y_1=y_2\)且都不是循环,则说明一定是某个边界上的格子坏了,并且我们此时很容易判断出坏掉的格子的方向
否则出现的一定是某个方案有循环而另一个方案不成循环
因为考虑坏掉的格子的方向是从编号大的指向编号小的,那么其在方案二的填法中一定不会成循环,反之则在方案一中一定会成环
下面我们就以这种情况为例,考虑此时如何确定方案一中坏掉的格子的编号\(j\)
不难发现如果此时我们改变初始位置\(i\)的编号,如果\(i\le j\)则此时会返回循环,否则就可以跳出循环
答案显然具有二分性,因此很容易确定出\(j\)的值,这个在方案二中也是同理,只不过是\(i\ge j\)会循环
那么现在我们已经知道了坏掉的格子的具体位置了,要确定它的方向也很容易,直接向下图一样再询问一次即可(非红色的格子的填法任意,中间那个就是坏掉的格子位置):
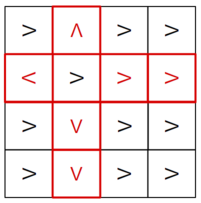
此时根据反馈的跳出位置可以很容易地判断方向了,而此法的询问总次数为\(2+\lceil \log(n^2)\rceil +1=17\),足以通过此题
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=105;
int n,cnt,rx[N*N],ry[N*N],x_1,y_1,x_2,y_2; char A[N][N],B[N][N];
inline void ask(char c[N][N],CI sx,CI sy,int& x,int& y)
{
printf("? %d %d\n",sx,sy);
for (RI i=1,j;i<=n;++i,putchar('\n'))
for (j=1;j<=n;++j) putchar(c[i][j]);
fflush(stdout); scanf("%d%d",&x,&y);
}
inline void answer(CI x,CI y,const char& ch)
{
printf("! %d %d %c\n",x,y,ch); fflush(stdout);
}
int main()
{
RI i; scanf("%d",&n); int x=1,y=1,dy=1,ret; bool flag=0;
while (x<=n)
{
rx[++cnt]=x; ry[cnt]=y;
if (flag&&(y==1||y==n)) A[x][y]='v'; else
if (dy==1) A[x][y]='>'; else A[x][y]='<';
if (flag&&(y==1||y==n)) ++x,dy*=-1,flag=0; else y+=dy,flag=1;
}
ask(A,1,1,x_1,y_1);
x=rx[cnt]; y=ry[cnt]; dy=y==1?1:-1; flag=0;
while (x>=1)
{
if (flag&&(y==1||y==n)) B[x][y]='^'; else
if (dy==1) B[x][y]='>'; else B[x][y]='<';
if (flag&&(y==1||y==n)) --x,dy*=-1,flag=0; else y+=dy,flag=1;
}
ask(B,rx[cnt],ry[cnt],x_2,y_2);
if (x_1==x_2&&y_1==y_2)
{
if (x_1==0) answer(1,y_1,'^'); else
if (x_1==n+1) answer(n,y_1,'v'); else
if (y_1==0) answer(x_1,1,'<'); else answer(x_1,n,'>');
return 0;
}
if (x_1==-1)
{
int l=1,r=cnt,mid; while (l<=r)
{
mid=l+r>>1; ask(A,rx[mid],ry[mid],x_1,y_1);
if (x_1==-1) ret=mid,l=mid+1; else r=mid-1;
}
} else
{
int l=1,r=cnt,mid; while (l<=r)
{
mid=l+r>>1; ask(B,rx[mid],ry[mid],x_2,y_2);
if (x_2==-1) ret=mid,r=mid-1; else l=mid+1;
}
}
x=rx[ret]; y=ry[ret];
for (i=1;i<x;++i) A[i][y]='^';
for (i=x+1;i<=n;++i) A[i][y]='v';
for (i=1;i<y;++i) A[x][i]='<';
for (i=y+1;i<=n;++i) A[x][i]='>';
ask(A,x,y,x_1,y_1);
if (x_1==0) answer(x,y,'^'); else
if (x_1==n+1) answer(x,y,'v'); else
if (y_1==0) answer(x,y,'<'); else answer(x,y,'>');
return 0;
}
Postscript
唉突然发现还有两周就要期末考了,接下来得好好复习下了
不过考完之后就是爽训时间,暑假开始可能要开始做Gym的真题来训练了,到时候可能也要拉上队友一起,训练下默契度啥的
总而言之还是加油吧,争取明年能打出些成绩的说