题目大意: 已知

a,b,c,d,n,m已知, 求f(n,m).
数据范围
1<=N,M<=10^1000 000,a<=a,b,c,d<=10^9
首先用到费马小定理将n和m缩小到int范围。
费马小定理
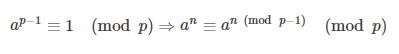
其中p为质数,a为不是p的倍数的正整数。
首先用到高中的数列。
F(n,m)=a·F(n,m-1)+b=(a^(m-1))F(n,1)+b+ab+...+(a^(m-2))b
=(a^(m-1))c·F(n-1,m)+(a^(m-1))d+b+ab+...+(a^(m-2))b
令p=b+ab+...+(a^(m-2))b, s=(a^(m-1))c, t=(a^(m-1))d+p, q=t+st+...+(s^(n-2))
F(n,m)=s·F(n-1,m)+t=(s^(n-1))F(1,m)+q=(s^(n-1))(a^(m-1)+p)+q
其中p和q都是等比数列,可以使用等比数列求和公式计算。注意a或s为1时不能用等比数列求和公式计算,此时p和q变成了等差数列,直接使用快速幂得出结果。
除法求模使用逆元来解决。
下面贴代码
#include <bits/stdc++.h> #define IO ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); using namespace std; const int mod = 1e9 + 7; int fastpow(int base, int n)//快速幂 { int ans = 1; while(n) { if(n&1) ans = (1ll * ans * base) % mod; base = (1ll* base * base) % mod; n >>= 1; } return ans; } signed main() { IO; string nn, mm; int a, b, c, d; int n = 0, m = 0, tn = 0, tm = 0; cin >> nn >> mm; cin >> a >> b >> c >> d; for (int i = 0; i < nn.length();i++) { n = (10ll * n + nn[i] - '0') % (mod - 1);//利用费马小定理缩小n tn = (10ll * tn + nn[i] - '0') % mod; } for (int i = 0; i < mm.length();i++) { m = (10ll * m + mm[i] - '0') % (mod - 1);//和缩小n同理,缩小m tm = (10ll * tm + mm[i] - '0') % mod; } n = (n - 1 + mod - 1) % (mod - 1); tn = (tn - 1 % mod) % mod; m = (m - 1 + mod - 1) % (mod - 1); tm = (tm - 1 + mod) % mod; int p, q, s, t, x, y; x = fastpow(a, m); s = 1ll * x * c % mod; y = fastpow(s, n); if(a-1) p = 1ll * b * (x - 1 + mod) % mod * fastpow(a - 1, mod - 2) % mod; else p = 1ll * tm * b % mod; t = (1ll * x * d + p) % mod; if(s-1) q = 1ll * t * (y - 1 % mod) % mod * fastpow(s - 1, mod - 2) % mod; else q = 1ll * tn * t % mod; cout << (1ll * y * (x + p) % mod + q) % mod << endl; return 0; }