最后修改日期:2023/10/17
简介
温度对电源的影响
半导体受温度的影响很明显,因此温度的变化会使得电源的输出电压变化,称为温度漂移(温漂)。
限制温度的影响
如果想要限制温度对电源的影响,一个思路就是:找到与温度正相关、负相关的电路,将二者的电压以合适的权重相加(线性电路满足叠加原理),这样总的电压的温度系数就被消去,因此总电路不受温度影响。
假设有两个关于温度线性变化的电路,不妨设它们各自的电压满足关系式:
\[\frac{\partial V_1}{\partial T}=C_1>0, \frac{\partial V_2}{\partial T}=C_2<0
\]
那么总是能找到一组系数\(\alpha_1, \alpha_2\),使得:
\[\alpha_1\frac{\partial V_1}{\partial T}+\alpha_2\frac{\partial V_2}{\partial T}=0
\]
因此二者的总电压就是与温度无关的:
\[V=\alpha_1V_1+\alpha_2V_2, \frac{\partial V}{\partial T}=0
\]
这样就实现了0温度系数的参考源电路。
带隙基准源
带隙基准源(Bandgap Reference)是精度较高、使用较多的一类参考源电路。其使用一个BJT的BE结(温度系数=-2 mV/℃)和一个热电压\(V_T\)偏差的电路(温度系数=0.085 mV/℃)。
求解一对面积之比为\(1:A\)的BE结
已知PN结的伏安表达式为
\[I=I_s(e^{\frac{V}{V_T}}-1), V_T=\frac{kT}{q}\approx26\text{ mV}@T=300\text{ K}
\]
当PN结正偏时,一般有\(V\gg V_T\),所以可以近似为
\[I\approx I_se^{\frac{V}{V_T}}
\]
反解得到
\[V=V_T\ln{\frac I{I_s}}
\]
带隙基准源电路1
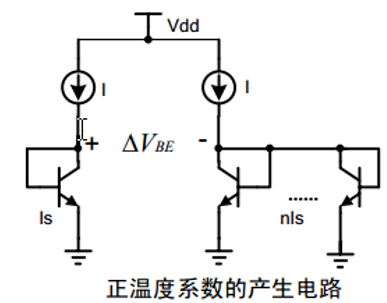
所以对于以上的电路有:
\[\Delta V_{BE}=V_{BE1}-V_{BE2}=V_T\ln{\frac I{I_s}-V_T\ln{\frac I{nI_s}}}=V_T\ln n
\]
\[\frac{\partial\Delta V_{BE}}{\partial T}=\frac kq \ln n
\]
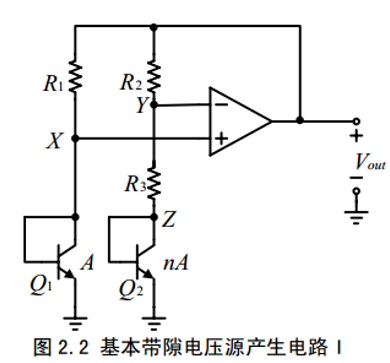
所以对于以上的电路有:
\[V_{XZ}=V_T\ln n
\]
由运放虚短容易得到:
\[\frac{V_{out}-V_X}{R_2}=\frac{V_X-V_Z}{R_3}=\frac{V_T\ln n}{R_3}
\]
解得:
\[V_{out}=V_X+\frac{R_2}{R_3}V_T\ln n=V_{BE1}+\frac{R_2}{R_3}V_T\ln n\tag{1}
\]
所以:
\[\frac{\partial V_{out}}{\partial T}=\frac{\partial V_{BE1}}{\partial T}+\frac{R_2k}{R_3q}\ln n=0\tag{2}
\]
最简化的半导体物理计算
根据半导体物理知识:
\[J_s\propto T^{3+\frac\gamma 2}\exp\left(-\frac{E_g}{kT}\right)=T^{3+\frac\gamma 2}\exp\left(-\frac{qV_{g}}{kT}\right)
\]
上式中,\(\gamma\)代表\(D_n/\tau_n\propto T^\gamma\),\(V_g\)是禁带宽度对应的电势差。不妨将正比系数定义为\(B\),则:
\[I_s=AJ_s=ABT^{3+\frac\gamma2}\exp\left(-\frac{V_g}{V_T}\right)
\]
\[I\approx I_s\exp\left(\frac V{V_T}\right)=ABT^{3+\frac\gamma2}\exp\left(\frac{V-V_g}{T}\right)\tag{3}
\]
参照的方法,假设一个已知的温度\(T_0\),这个温度下的所有量都加上下标 “0”:
\[I_0=ABT_0^{3+\frac\gamma2}\exp\left(\frac{V_0-V_{g0}}{T_0}\right)\tag{4}
\]
这里假设\(V_g=V_{g0}\),将\((3)\)与\((4)\)相除,得到:
\[\frac{I}{I_0}=\left(\frac T{T_0}\right)^{3+\frac\gamma 2}\exp\left(\frac{V-V_g}{V_T}-\frac{V_0-V_g}{V_{T0}}\right)
\]
反解得到:
\[V=V_g+\frac T{T_0}(V_0-V_g)+V_T\ln\frac I{I_0}-\left(3+\frac\gamma 2\right)V_T\ln\frac{T}{T_0}\tag{5}
\]
只考察电压的变化,因此假设\(I\approx I_0\),则第三项为0。然后注意到,第四项是对数函数,相较于第二项一次函数来说很小,可以忽略。所以\((5)\)化为:
\[V=V_g+\frac T{T_0}(V_0-V_g)\tag{6}
\]
以上求得的是一个PN结的电压,可以是BJT的\(V_{BE}\)。取合适的参数值可以使得\((2)\)成立,即:
\[\frac{V_0-V_g}{T_0}+\frac{R_2}{R_3}\frac kq\ln n=0\implies\frac{R_2}{R_3}\frac{k T}{q}\ln n=-\frac{T}{T_0}(V_0-V_g)\tag{7}
\]
代入\((1)\),得到:
\[V_{out}=V_{BE}+\frac{R_2}{R_3}V_T\ln n=\textcolor{red}{V_g}\tag{8}
\]
由此可知,带隙基准源的输出点电压就是\(V_g\),这只与半导体的禁带宽度(带隙)有关(对于硅,\(V_g=1.170\text{ V}\)),这也是其名称的来源。
简化是否合理
以上计算过程用到了多处简化。
禁带宽度近似于温度无关
其实禁带宽度与温度是有关的。由半导体物理可知公式:
\[E_g(T)=E_g(0)-\frac{\alpha T^2}{T+\beta}\implies V_g(T)=V_g(0)-\frac{\alpha T^2}{q(T+\beta)}
\]
对于硅半导体,有\(\alpha=4.73\times10^{-4}\text{ eV/K}, \beta=636\text{ K}, V_g(0)=1.170\text{ V}\)。
一般温度在300K量级,因此\(V_g(0)-V_g(300)=0.0455\text{ V}\),相较于1.170 V来说还是很小的,因此认为\(V_g\)不变也是合理的。
对数项是否可以省略
考察\((5)\to(6)\)的省略是否合理。将\((5)\)的最后一项进行一阶Taylor展开:
\[-\left(3+\frac\gamma 2\right)\frac{kT}{q}\ln\frac T{T_0}=\frac{k(6+\gamma)(T-T_0)}{2q}+O(T-T_0)^2\approx\left(3+\frac\gamma 2\right)V_T\frac{T-T_0}{T}
\]
不妨假设\(V_T\sim(V_0-V_g)\)。但有$\frac{T}{T_0}>1, \(\frac{T-T_0}{T}<1\)。当\(T_0\)接近\(T\)时,后者会接近于0,比前者小很多,因此可以省略。
实际上PN结不满足Shockley方程
根据半导体物理,硅材料的PN结在电流不小的时候是不满足如\((9)\)所示的Shockley方程的:
\[J=J_s\left(\exp\left(\frac{qV}{kT}\right)-1\right)\tag{9}
\]
实际上正向大电流满足的公式如\((10)\)所示:
\[J_F\propto \exp\left(\frac{qV}{mkT}\right), m\in[1,2]
\]
如果这样的话以上计算就都不成立了。不过实际上在半导体物理里面也就只是提到了这个效应,在理论计算时该用Shockley方程还是会用的。所以这里也就不纠结这种细节了。

