A Simple Task
离线 + 线段树。
我们考虑建立 \(26\) 棵线段树, 每棵线段树叶子节点储存的信息为 在当前字符串中当前位置的字符是否为 该线段树所代表的字符。 这样的话, 我们可以 \(n \log(n)\) 查询一定区间内字符的个数。 我们考虑类似于 \(01\) 串排序的方式, 对于升序而言, 先将修改区间内字典序较小的字符赋值在最左侧尚未赋值的区域, 这样进行 \(26\) 次赋值操作即可。 总时间复杂度为 \(O(26 n\log(n))\)。
Tax
差分优化建图。
对于两条边相连的三个点 \(u - v - k\), 设两条边的权值分别为 \(w_1, w_2\), 那么 我们有边 \(u - k\) 的权值为 \(\max(w_1, w_2)\)。 故而我们可以建立 \(O(m^2)\) 条边, 跑最短路即可。
考虑减少边数。 实际上,一个点的很多边彼此有着联系,对于一条边 \(u - v\) (设权值为 \(w\) ),\(v\) 点连出的所有比 \(w\) 小的边都是 \(w\) 本身,而对于比 \(w\) 大的边,增长的值为两边的差值。
我们考虑以这样的形式减少边数 :
-
先将一条边拆成两个点 \(i,i'\),以原边边权连接,并分属于边的两个端点。
-
原图同一点的相邻的边,其中两条为 \(i,j\) ,假设 \(w_i < w_j\), 连边 \(i→j\),权值为 \(w_j - w_i\) 连边 \(j→i\),权值为 \(0\);
-
新建源点 \(s\),向所有原图 \(1\) 点的出边 \(i\),连接 \(s→i\),权值为 \(val_i\)
通过排序后差分建图, 边数减少到 \(O(m)\), 总时间复杂度为 \(O((n + m) \log m)\)。
Minimal Coverage
考虑到线段覆盖的区间越大, 所有线段能够安放下的概率越大。 我们考虑二分答案枚举 区间覆盖的大小。
对于二分的判定, 我们有两种方式 : DP 或者 bitset 维护。
对于 DP 而言, 我们其实只关心两个线段链接处的转折点(即两个相距最远的转折点可以确定区间的覆盖范围)。 我们令 \(dp(i, j)\) 表示在只考虑前 \(i\) 个线段的情况下, 是否能在 \(j\) 处存在转折点。 每次添加线段的时候, 其实是将所有为 \(1\) 的点向左 或 向右平移, 并且抛弃大于 \(mid\) 小于 \(0\) 的点。 初状态 \(dp(0, 0 - mid) = 1\), 表示这之间的点都可以作为起始点。 末状态只用判断 \(dp(n, 1 - mid)\) 中是否有 \(1\) 即可。
用 bitset 则和 dp 的思路类似, 只是将 dp 的思路 用模拟的角度展现 出来。
Xor of 3
首先考虑到每次操作对整个序列的异或和没有影响, 即对于修改后的三个数而言, 他们的异或和不变。
那么我们首先可以求整个序列的异或和。 倘若异或和不为 \(0\), 则一定无解。
在经过一系列特殊变换后, 原题其实等价于 :
给定 \(s_0, s_1,⋯s_n\),保证 \(s_0 = s_n = 0\),每次操作可以选定一个数 \(i \in [1, n]\),使得 \(s_{i + 1} ← s_{i - 1}\), \(s_i ← s_{i + 2}\), 要求
n 次操作后最终所有数变为 \(0\)。
这就很好做了。显然每次赋值都只能在下标奇偶性相同的相邻位置上进行,且不能给 \(s_0, s_n\) 赋值,那么只需要分下标的奇偶即可。下标为偶数的位置显然无论如何都可以被赋值成 \(0\) ,那么先考虑奇数位置:找到数值为
\(0\) 的位置,然后向两边赋值即可,找不到即无解。
Relay Race
原题等价为找两条 从 \((1, 1)\) 到 \((n, n)\) 的路径, 使得两条路径的权值和最大, 每个格子的权值只能计算一次。
我们可以直接用四维状态来表示每条路径的位置, 这样时间 和 空间都是 \(O(n ^ 2)\) 无法接受。
考虑到两条路径是同步进行的, 即向下 和 向右走的步数和相同, 因此我们可以仅凭步数和 和 横纵坐标之一 来确定该点的坐标, 时间复杂度优化到 \(O(n ^ 3)\)。
Perfect Groups
先证明一个结论 :
若 \(a \times b = x ^ 2, b \times c = y^2\) 那么 \(a \times c = z^2\)
简单来看, \(a \times c = \dfrac{x^2 \times y^2}{b^2}\)。 由于 \(b | x^2\) 并且 \(b | y^2\), 所以 \(b ^ 2 | x ^2y^2\)。 故此 \(ac\) 一定是完全平方数。
维护一个并查集,若 \(a_i \times a_j\) 为完全平方数那么就把他们塞到一个集合里,那么问题就变成了区间有多少个集合。
总时间复杂度为 \(O(n^2)\)。
Range Harvest Query
对于一个区间 \([L, R]\), 我们令当前时间为 \(t\), 上一次收割整个区间的时间为 \(t_0\), 那么此次的收获量为 \((t - t_0) \times \dfrac{(R - L + 1) \times (L + r)}{2}\)。
那么, 我们所需要维护的是每个区间上一次被收割的时间。 区间数过多, 但询问数只有 \(2 \times 10^5\), 即最多会有 \(4 \times 10^5\) 个独立的区间。
我们考虑用 珂朵莉树 来维护这个过程。 对于一个大区间, 将询问区间分离出来, 将 大区间 分裂成三个小区间, 再分别维护上一次修改的时间即可。
Median Pyramid Hard
二分转化为 01 序列。
观察 01 序列最终的结果
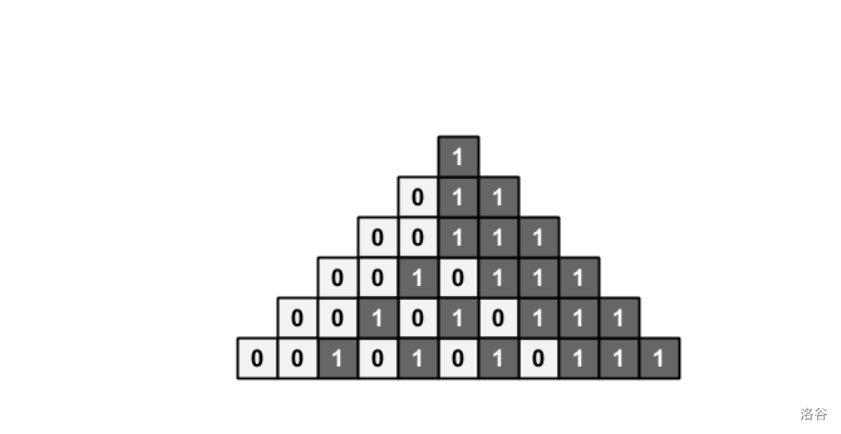
我们发现, 如果有两个 \(1\) 或 两个 \(0\) 挨在一起, 他们会一起裹挟向上走。
且越靠经序列的正中间, 越有可能成为答案。 因此, 我们可以 \(O(n)\) 枚举整个 序列, 找到离正中间最近的相邻的 \(0\) 或 \(1\), 依次来快速判断二分的解。
遥远的国度 && Jamie and Tree
如果不考虑换根的操作, 实际上是一个树链剖分模板题。
我们不妨以 \(1\) 为根树链剖分, 预处理出我们要求的一些值。
对于换根操作, 我们考虑其相对于以 \(1\) 为根时的变化。
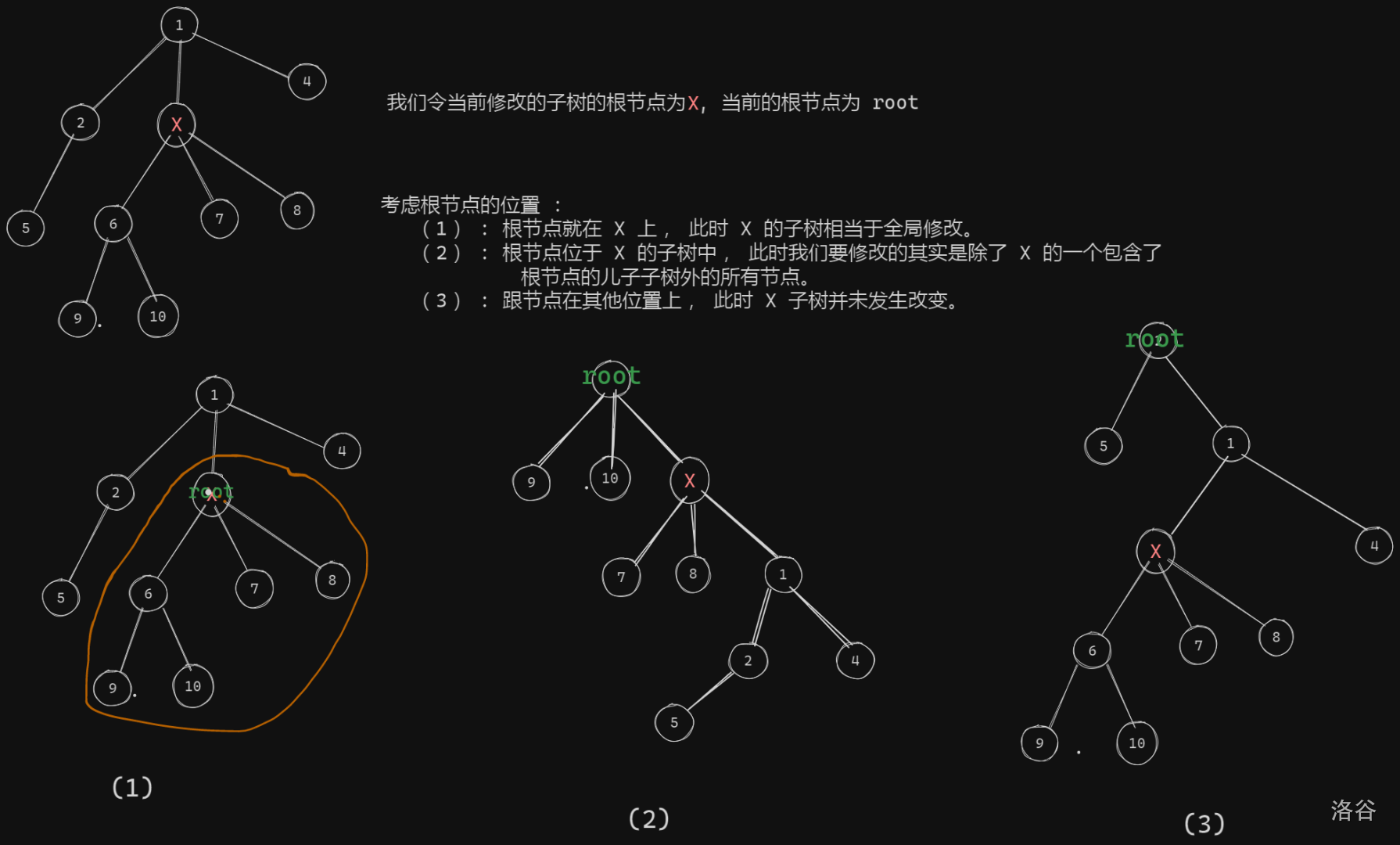
故此, 我们可以只针对子树问题进行分讨, 在 保证实际上原树一直以 \(1\) 为根的基础上进行正确的操作。
此外, 对于两个点的最近公共祖先的问题, 我们也需要进行类似的讨论 :
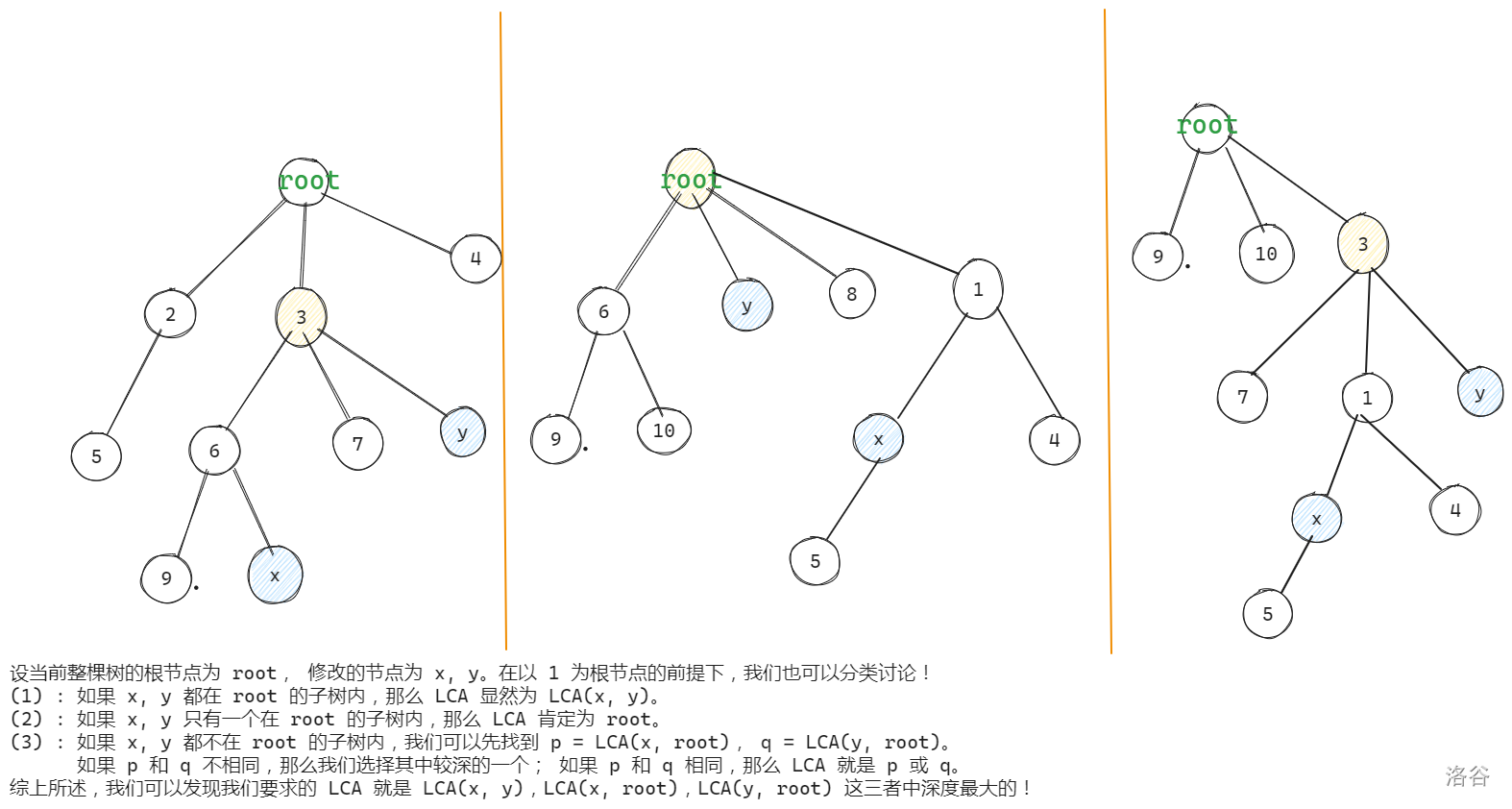
当解决完这些问题后, 本题也就迎刃而解了。
Naptime G
我们首先考虑只为一条链的情况, 显然可以通过 DP 的方式求解。 令 \(dp(i, j, 0 / 1)\) 表示在 \(i\) 时刻, 已经睡了 \(j\) 小时, 当前时刻是否在睡觉。
转移方程即为 :
dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1]);
dp[i][j][1] = max(dp[i - 1][j - 1][0], dp[i - 1][j - 1][1] + a[i]);
再考虑到环的情况, 我们可以发现, 它与链的差别主要在于 它可以横跨链的前后两端, 故而我们可以考虑直接固定选择 \(1\) 和 \(n\) 两点, 那么此时和链的转移类似。
Chess Strikes Back
我们考虑将每个 \(2 \times 2\) 的方格看成一个小矩阵, 发现每个小矩阵中只能放置且必须放置一个 棋子 且 每个小矩阵中只有两个位置能放置棋子。
每一个小矩阵有 \(4\) 中状态 :
-
没有限制, 两个格子都可以放置棋子。
-
只有右下能放, 记这个小矩阵为一个 L 点。
-
只有左上能放, 记这个小矩阵为一个 R 点。
-
都不能放, 显然为NO。
对于每个 L 点而言, 它的影响是在它左上方的所有小矩阵必须也是 L 点。
对于每个 R 点而言, 它的影响是在它右下方的所有小矩阵必须也是 R 点。
故而我们可以得出本题无解的充要条件 :
-
存在一个小矩阵其中两个白色格子都被去掉。
-
存在一个 L 点 和 一个 R 点满足 R 点 在 L 点的左上方。
我们考虑以 行 为准建立线段树, 维护每一行中 最左端 R 点 和 最右端 L 点的列数, 在行 与 行的合并时判断是否无解。
Substrings in a String
神秘 bitset 科技 。

对于修改操作,我们只需要修改对应 bitset 的 01 值即可。
Omkar and Forest
对于每个可以填非负整数的格子,设共有 \(k\) 个,可以填 \(0\) 或填正整数。选其中一部分填 \(0\),另一部分填正整数,有 \(2^k\) 种选法,每种选法贡献独立。
对于每个原来就是 \(0\) 或选后是 \(0\) 的格子,它们周围不是 \(0\) 的格子只能填 \(1\),因为只能填非负整数,且已经不能填 \(0\),填的数字如果大于 \(1\),与 与它相邻有 \(0\) 的格子 的绝对差就大于 \(1\)。
同理可填出 \(2,3,4,\dots\) 发现每种选法的贡献都只有 \(1\) ,所有答案就是选法的总数,特判全图原来没有 \(0\) 的情况。
Lomsat gelral
树上启发式合并。
对于这道题, 我们考虑暴力的方式, 每次遍历整颗子树, 并记录每种颜色出现的次数。 每次统计完成后都要将数组清空, 来防止子树间互相影响。 但是我们实际上可以保留最后一次遍历的数组, 毕竟我们当前父节点所代表的子树 一定 包含当前子树。 考虑保留节点数最多的子树, 即求重儿子。
这样看似没有得到很多优化的方式, 实际上使整个算法的复杂度变为 \(O(n \log n)\)。
关于复杂度证明:
对于每个节点,它被计算的次数就是它到根节点路径上的轻边(连到轻儿子的边)数, 故而我们只需算出轻边有几条。
由于每从一个深度为 \(dep\) 的节点沿一条轻边走到深度 \(dep - 1\) 的节点,子树大小就至少 \(\times 2\) (这是因为有一个重儿子的大小 \(\ge\) 当前子树)
所以最多只有 \(\log n\) 条轻边!
RAJ-Rally
种树
Ball Machine
由于我们主要考虑的是子树的问题, 故而采用线段树 + dfs序 的方式维护每个子树所能容纳的球的个数。
对于操作 \(1\) 来讲, 我们考虑类似于 BST 上查询排名的方式来得到最后一个球的位置。
对于操作 \(2\) 来讲, 我们考虑倍增地计算要修改的节点上方 最早的储存了球的祖先节点, 那么对于这个问题来讲, 直接将该祖先节点变为空即可。
Small Multiple
我们考虑数位和的变化,将其抽象成对 \(1\) 进行 \(+ 1\) 和 \(\times 10\) 两种操作, 显然, 通过这两种方式我们可以得到任意一个数。
对于本题来讲, 由于我们要求最小的数位和使得 其组成的数 为 \(K\) 的倍数, 那么实际上我们所求即为 使用最少的 \(+1\) 操作使得我们得到的数 \(\bmod K = 0\)。 我们考虑用 01bfs 求解, 由于我们最多只会将 \(1 \sim K - 1\) 中的所有数遍历一次, 即我们的时间复杂度为 \(O(K)\)。
Good Graph
我们考虑离线处理,在得到加入所有边的图后建立按照读入顺序为第一关键字的生成树,这些边由于树不存在环一定满足题意。
那么此时,问题即为:给定一棵树,判断向树中加入一些边 而 构成的环的异或和是否为 \(1\)。

The Shortest Statement
我们观察数据范围,发现 \(m - n \le 20\), 那么本题等价于:给定一棵树,然后添加不超过 \(20\) 条边,求全源最短路。
那么,我们首先求出原图的最小生成树,利用树上差分得到树上任意两点间的距离。对于每一条边的两个端点,我们在原图上跑 dijkstra 计算单源最短路,表示
必须经过该点时所得的最短路径。
最后将答案取最小值即可,时间复杂度为 \(O(40 \times n\log n)\)。