D - Poisonous Full-Course(DP)
题意
现在有 \(N\) 道菜,高桥需要依次享用。第 \(i\) 道菜有两个属性 \((X_i,Y_i)\),其意义是:
- 若 \(X_i=0\),则第 \(i\) 道菜是解毒的,其美味度为 \(Y_i\);
- 若 \(X_i=1\),则第 \(i\) 道菜是有毒的,其美味度为 \(Y_i\)。
当高桥享用一道菜,他的状态变化如下:
- 初始时,高桥的胃是健康的。
- 当高桥的胃是健康的,
- 如果他吃了一道解毒的菜,他的胃仍是健康的;
- 如果他吃了一道有毒的菜,他的胃会变为不适的。
- 当高桥的胃是不适的,
- 如果他吃了一道解毒的菜,他的胃会变为健康的;
- 如果他吃了一道有毒的菜,他会死亡。
他享用菜品的过程如下:
- 对 \(i=1,2,\dots,N\),循环下面的过程:
- 首先,上第 \(i\) 道菜;
- 然后,高桥选择「享用」或「跳过」这道菜:
- 如果他选择「享用」这道菜,那么他的状态会同时按上面所说的方式变化。
- 如果他选择「跳过」这道菜,那么这道菜会被丢弃。
- 最后,如果他享用这道菜后没有死亡,或者跳过了这道菜,
- 如果 \(i\ne N\),那么他会继续对第 \(i+1\) 道菜进行此过程。
- 如果 \(i=N\),那么他就成功活着离开了餐馆。
请你求出:在高桥活着离开餐馆的情况下,他选择「享用」的菜品的美味度之和的最大值。如果他所有菜都「跳过」则美味度之和为 \(0\)。
\(1\le N\le3\times10^5\),\(X_i\in\{0,1\}\),\(-10^9\le Y_i\le10^9\)。保证所有输入为整数。
注意答案可能超过 32 位整数的范围。
思路
类似没有上司的舞会,我们考虑 DP。设 \(f(i,0/1)\) 表示前 \(i\) 道菜,当前胃是 \(0\) 健康的 / \(1\) 不适的,能获得的最大美味度之和。
由于开始时胃是健康的,所以 \(f(0,1)=-\infty\)。答案 \(\max\{f(N,0),f(N,1)\}\)。
时间 \(O(N)\)。
代码
可以滚动数组做到 \(O(1)\) 空间,不过要注意先取 \(\max\)。
#include <iostream>
#define f(x, y, z) for (int x = (y); x <= (z); ++x)
#define int ll
using namespace std;
typedef long long ll;
const int N = 3e5 + 10;
const int INF = 0x3f3f3f3f3f3f3f3f;
int n, f[2];
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
f[1] = -INF;
f(i, 1, n) {
int x, y; cin >> x >> y;
if (!x) f[0] = max(f[0], max(f[0], f[1]) + y);
else f[1] = max(f[0] + y, f[1]);
}
cout << max(f[0], f[1]) << '\n';
return 0;
}
E - Best Performances(std::multiset 的应用)
题意
有一个长度为 \(N\) 的序列 \(A\),初始时每一项都为 \(0\)。给定 \(K\le N\),令 \(f(A)\) 表示 \(A\) 中前 \(K\) 大的数之和。
对 \(A\) 进行 \(Q\) 次修改,第 \(i\) 次修改把 \(A_{X_i}\) 改为 \(Y_i\)。每次修改后,输出 \(f(A)\)。
\(1\le K\le N\le5\times10^5\),\(1\le Q\le5\times10^5\)。\(1\le X_i\le N\),\(0\le Y_i\le10^9\)。保证所有输入均为整数。
思路
建两个 multiset<pair<int, int> > \(a\) 和 \(b\),分别维护 \(A\) 中前 \(K\) 大的数和剩余的 \(N-K\) 个数。保存的第一维(pair 自动按第一维比较大小)是元素的值,第二维是下标,以方便查找。
当修改 \(A_{X_i}\) 为 \(Y_i\) 时,我们考虑先修改再维护。
具体地,我们在两个 multiset 中查找 \((A_{X_i},X_i)\) 并删除(肯定在两个中的一个里),然后在同一个集合中加入 \((Y_i,X_i)\),同时保存 \(A_{X_i}\) 便于之后查找。
现在 \(a\) 中不一定是前 \(K\) 大的数,我们判断 \(a\) 的最小值是否大于等于 \(b\) 的最大值,如果不满足则交换。(有点类似对顶堆维护动态中位数的思想)
至于 \(f(A)\),在维护 \(a\) 时一起修改即可。
时间 \(O(Q\log N)\)。
代码
注意判断 multiset 是否为空,否则会 RE。注意答案开 long long,否则会 WA。(别问我怎么知道的)
#include <set>
#include <iostream>
#define f(x, y, z) for (int x = (y); x <= (z); ++x)
using namespace std;
typedef pair<int, int> pii;
const int N = 5e5 + 10;
int n, k, q, c[N];
long long s;
multiset<pii> a, b;
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> k >> q;
f(i, 1, k) a.insert({0, i});
f(i, k + 1, n) b.insert({0, i});
while (q--) {
int x, y; cin >> x >> y;
if (!a.empty() && a.find({c[x], x}) != a.end()) {
a.erase({c[x], x});
s -= c[x];
a.insert({c[x] = y, x});
s += y;
} else {
b.erase({c[x], x});
b.insert({c[x] = y, x});
}
while (!a.empty() && !b.empty() && (*a.begin()).first < (*--b.end()).first) {
auto i = *a.begin(), j = *--b.end();
a.erase(a.begin()), b.erase(--b.end());
a.insert(j), b.insert(i);
s -= i.first;
s += j.first;
}
cout << s << '\n';
}
return 0;
}
F - Merge Sets(二维偏序)
题意
对于两个由整数构成的集合 \(A,B\) 满足 \(A\cap B=\varnothing\),我们定义 \(f(A,B)\) 如下:
- 令 \(C=\{C_1,C_2,\dots,C_{|A|+|B|}\}\) 表示 \(A\cup B\) 按升序排序后的序列。
- 令 \(k_1,k_2,\dots,k_{|A|}\) 表示 \(A\) 的各项在 \(C\) 中的下标,即 \(A=\{C_{k_1},C_{k_2},\dots,C_{k_{|A|}}\}\)。
- \(f(A,B)=\displaystyle\sum_{i=1}^{|A|}k_i\)。
现在给定 \(N\) 个由整数构成的集合 \(S_1,S_2,\dots,S_N\),每个集合的大小为 \(M\),且保证对任意 \(i\ne j\),\(S_i\cap S_j=\varnothing\)。
设 \(S_i=\{A_{i,1},A_{i,2},\dots,A_{i,M}\}\)(在数据范围和输入格式中用到)。
请求出 \(\displaystyle\sum_{1\le i<j\le N}f(S_i,S_j)\)。
\(1\le N\le10^4\),\(1\le M\le10^2\),\(1\le A_{i,j}\le 10^9\)。保证若 \(i_1\ne i_2\) 或 \(j_1\ne j_2\),则 \(A_{i_1,j_1}\ne A_{i_2,j_2}\)。保证所有输入均为整数。
思路
首先把所有数离散化,那么值域变为 \([1,N\times M]\),可以发现这并不影响答案。
先来考虑两个集合 \(A,B\) 的 \(f(A,B)\) 怎么求。
我们可以把集合中的每个数的大小看做高度,那么 \(A_i\) 的排名即为在 \(A_i\) 下方的 \(B\) 中的点的数量加上 \(A_i\) 在 \(A\) 中的排名。
由于 \(A\) 和 \(B\) 是前后顺序的,我们不妨放到平面上考虑:
设 \(A=\{2,4,1,7\}\),\(B=\{3,8,6,5\}\)。我们把这些点画在平面上,如下图:(红点是 \(A\),蓝点是 \(B\))
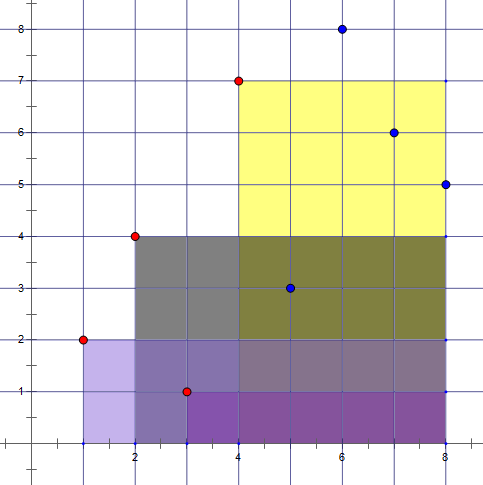
可以看到,在 \(A_i\) 右下方范围内的蓝点数量即为小于 \(A_i\) 的 \(B\) 中数的数量。
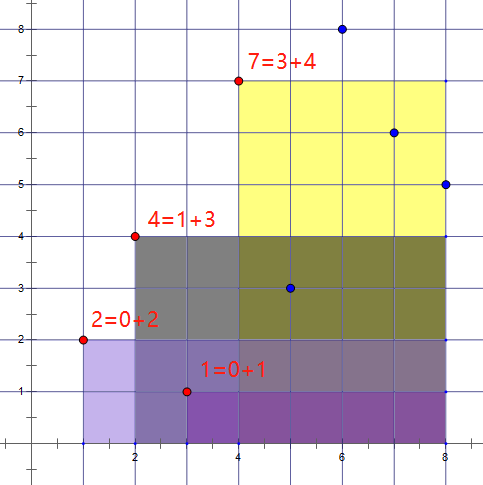
于是每个 \(A_i\) 的贡献可以拆成两部分:在 \(A_i\) 右下方的蓝点数量、\(A_i\) 在 \(A\) 中的排名是第几小。如下图:
那么对于许多个集合,我们同样可以这样来求:
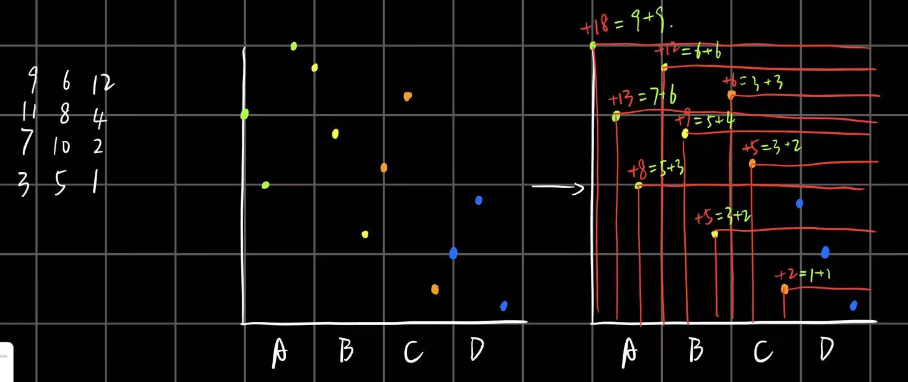
每个点的贡献:在它右下方且不与它在同一个集合的点的数量,加上它在自己集合中的排名乘以后面还有几个集合。
于是我们从右到左、从上到下(为了消除同一集合中的点的影响)遍历所有点,用树状数组维护高度即可。
时间复杂度 \(O(NM\log(NM))\)。
代码
#include <iostream>
#include <algorithm>
#define f(x, y, z) for (int x = (y); x <= (z); ++x)
#define g(x, y, z) for (int x = (y); x >= (z); --x)
using namespace std;
const int N = 1e4 + 10, M = 110;
int n, m, a[N][M], val[N * M], cnt, c[N * M], ans;
inline int lb(int const &x) { return x & (-x); }
void add(int x) { while (x <= n * m) ++c[x], x += lb(x); }
int sum(int x) { int r = 0; while (x) r += c[x], x -= lb(x); return r; }
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
f(i, 1, n) f(j, 1, m) cin >> a[i][j], val[++cnt] = a[i][j];
sort(val + 1, val + cnt + 1); //离散化
f(i, 1, n) f(j, 1, m) sort(a[i] + 1, a[i] + m + 1), a[i][j] = lower_bound(val + 1, val + cnt + 1, a[i][j]) - val;
g(i, n, 1) g(j, m, 1) ans += sum(a[i][j]), add(a[i][j]), ans += (i - 1) * j;
cout << ans << '\n';
return 0;
}