优化建图
发现并没有人写得很详细的样子,那我也摆烂好惹
前言
众所周知,连边的时间复杂度一般是 \(O(1)\),但,当连边的对象是一个连续的树上区间的时候,我们或许有更优的连边方式:优化建图。
前置知识:
-
树链剖分
-
线段树
-
树上倍增
-
Dijkstra
线段树优化建图
线段树优化建图,借助线段树这种数据结构,达到“以空间换时间”的目的,往往与树链剖分一起使用。
线段树的边分两类:
-
向上连的边,表示连出。
-
向下连的边,表示连入。
为什么这样规定?

如图。
单点连区间
我觉得上图讲的还是一目了然的,就是这样连啦。
当然也不一定是连到外面:

在本图中,这样的连边就代表着连 \(1\) 到 \([3,8]\) 的边。
区间连区间
建最开始的那个图的两个线段树,并建立一个虚点,上连线段树的区间连向虚点,虚点连向下连线段树。
最后,线段树优化建图,点数是 \(n\),边数是 \(nlogn\),带入即可计算时间复杂度。
例题
[JOISC 2022 Day1] 监狱
题目背景
JOISC 2022 D1T1
题目描述
在 JOI 王国,安保最严格的地方就是 IOI 监狱。IOI 监狱中有 \(N\) 个房间,以 \(1,\dots,N\) 编号。其中有 \(N-1\) 条通道。第 \(i\) \((1\le i\le N-1)\) 条通道双向地连接房间 \(A_i\) 和 \(B_i\)。任意两个房间都可以相互到达。
IOI 监狱中有 \(M\) 个囚犯,以 \(1,\dots,M\) 编号。第 \(j\) \((1\le j\le M)\) 个囚犯的卧室和工作室分别是房间 \(S_j,T_j\)。一个囚犯可能在另一个囚犯的卧室工作。然而,每个房间最多成为一个囚犯的卧室,一个囚犯的工作室。
一天早上,这 \(M\) 个囚犯需要从他们的卧室移动到他们的工作室。典狱长 APIO 先生需要按如下方式指示囚犯移动:
- 指令:选择一个囚犯,然后命令他从当前所在的房间移动到一个与该房间有直接连边的房间。为了避免囚犯交流,不允许将囚犯移动到有其他囚犯在的房间。
为了尽早开始工作,APIO 先生想知道,是否存在一种给出任意条指令的方案使得每个囚犯以最短路径从卧室到达工作室。
请编写一个程序,在给定如上房间、通道和罪犯的所有信息后判断是否存在满足条件的方案。
输入格式
每个测试数据包含多组测试用例。
第一行一个整数 \(Q\),表示这个测试数据包含 \(Q\) 组测试用例。
对于每组测试用例:
第一行一个整数 \(N\),表示房间个数。
接下来 \(N-1\) 行每行两个整数 \(A_i,B_i\) 表示通道连接房间的编号。
接下来一行一个整数 \(M\) 表示囚犯个数。
接下来 \(M\) 行,每行两个整数 \(S_i,T_i\) 表示囚犯的卧室和工作室。
输出格式
输出 \(Q\) 行,第 \(i\) 行表示对于第 \(i\) 组测试用例,如果存在一种满足题意的方案,输出 Yes,否则输出 No。
样例 #1
样例输入 #1
1
8
1 2
2 3
3 4
4 5
5 6
6 7
7 8
2
3 4
4 8
样例输出 #1
Yes
样例 #2
样例输入 #2
2
7
1 2
2 3
3 4
4 5
3 6
6 7
2
4 1
5 7
4
1 2
1 3
1 4
3
2 3
3 4
4 2
样例输出 #2
Yes
No
提示
【样例解释 #1】
可以通过发送如下指令完成任务:
- 让囚犯 \(2\) 从 \(4\) 号房间移动到 \(5\) 号房间。
- 让囚犯 \(1\) 从 \(3\) 号房间移动到 \(4\) 号房间。
- 让囚犯 \(2\) 从 \(5\) 号房间移动到 \(6\) 号房间。
- 让囚犯 \(2\) 从 \(6\) 号房间移动到 \(7\) 号房间。
- 让囚犯 \(2\) 从 \(7\) 号房间移动到 \(8\) 号房间。
这组样例满足所有子任务的限制。
【样例解释 #2】
这组样例满足子任务 \(1,3,4,5,6,7\) 的限制。
【数据范围】
对于所有数据,满足:
- \(1\leq Q\leq 1000\)。
- \(1\leq N\leq 120000\)。
- \(1\leq A_i\lt B_i\leq N\) \((i\in [1,N-1])\)。
- \(2\leq M\leq N\)。
- \(1\leq S_i,T_i\leq N\) \((i\in [1,M])\)。
- \(S_i\) \((i\in[1,M])\) 互不相同。
- \(T_i\) \((i\in[1,M])\) 互不相同。
- \(S_j \ne T_j\) \((j\in [1, M])\)。
- 任意两个房间之间可以通过给定道路互相到达。
- 对于所有测试用例,\(N\) 的总和不超过 \(120000\)。
详细子任务附加限制及分值如下表所示:
| 子任务编号 | 附加限制 | 分值 |
|---|---|---|
| \(1\) | \(A_i=i,B_i=i+1~(i\in[1,N-1])\) | \(5\) |
| \(2\) | \(Q\leq 20, N\leq 250, M=2\) | \(5\) |
| \(3\) | \(Q\leq 20, N\leq 250, M\leq 6\) | \(16\) |
| \(4\) | \(Q\leq 20, N\leq 250, M\leq 100\) | \(28\) |
| \(5\) | \(Q\leq 20, M\leq 500\) | \(12\) |
| \(6\) | 任意两个房间之间都可以通过不超过 \(20\) 条道路到达。 | \(11\) |
| \(7\) | 无附加限制 | \(23\) |
解题:
题意概括:
对于 \(n\) 个点的树,有 \(m\) 条起点与终点各不相同的行进路线形如 \(s_i\to t_i\),允许从某个点移动至相邻点,问能否在不存在某个点所在人数 \(> 1\) 的情况下完成所有行进路线。
首先有一个特别性质:
如果合法,一定有一种合法的方案使得每个人都是不停留地从头走到尾。
如果 \(A\) 走到道路一半需要等待 \(B\) 走完自己再走,那么我们自然也可以让 \(B\) 先走完,自己再走。
因此就有两限制:
-
\(A\) 起点在 \(s_B\to t_B\) 时,\(A\) 点先走。
-
\(A\) 终点在 \(s_B\to t_B\) 时,\(B\) 点先走。
而当存在冲突时,我们就输出 No。
因此我们可以规定将 \(m\) 个行进路线是 \(m\) 个点,\(A\) 先于 \(B\) 走是 \(A\) 向 \(B\) 连边,而存在冲突则是出现环。
需要判断一个图是否是有向无环图,拓扑排序即可。
考虑优化:
最主要的时间复杂度在于建图,就是判断上面的两条性质,对于每个点判断两条性质的时间复杂度是 \(O(n^2)\),我们考虑让一个行进计划一次性连好边:
-
复制原图的树为两棵新树 \(S,T\)。
-
将第 \(i\) 个行进计划在 \(S\) 上的对应点全都向 \(i\) 连边,表示起点在这些点的行进计划要先于 \(i\) 走。
-
将 \(i\) 向第 \(i\) 个行进计划在 \(T\) 上的所有对应点连边,表示终点在这些点的行进计划要晚于 \(i\) 走。
因此可以进行树链剖分+线段树优化建图。
时间复杂度 \(O(n\log^2 n)\)。
(tips:对于普通 dfs 树上建边和各个行进计划之间的边,最好开两个结构体存边或者开一个容器开一个结构体,总之不要放在一起存,否则会冲突)
Miku's Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register int
#define next Miku
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
namespace io{
// char in[1<<20],*p1=in,*p2=in;
// #define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
il int read(){
char c=getchar();
int x=0,f=1;
while(c<48)<%if(c=='-')f=-1;c=getchar();%>
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
il void write(int x){
if(x<0)<%putchar('-');x=~x+1;%>
if(x>9) write(x/10);
putchar(x%10+'0');
}
il int ins(char *str){
int len=0;
while(1){
char c=getchar();
if(c!='\n' && c!='\0' && c!='\r') str[++len]=c;
else break;
}
return len;
}
}
namespace mystd{
il int Max(int a,int b)<%if(a<b) return b;return a; %>
il int Min(int a,int b)<%if(a>b) return b;return a; %>
il int Abs(int a)<% if(a<0) return a*(-1);return a; %>
il double fMax(double a,double b)<%if(a<b) return b;return a; %>
il double fMin(double a,double b)<%if(a>b) return b;return a; %>
il double fAbs(double a)<% if(a<0) return a*(-1);return a; %>
il int dcmp(double a){
if(a<-eps) return -1;
if(a>eps) return 1;
return 0;
}
}const int maxn=1200500;
int T,n,m;
int dep[maxn],myf[maxn],sonum[maxn],top[maxn],hson[maxn],in[maxn],myin[maxn],tim;
int pos[maxn],du[maxn];
int t,head[maxn<<6];
vector<int> E[maxn];
struct edge{
int v,next;
};edge e[maxn<<6];
il void add_edge(int u,int v){
e[++t].v=v;
e[t].next=head[u];
head[u]=t;
}
namespace SegementTree{
#define lid (id<<1)
#define rid (id<<1|1)
int S[maxn<<2],T[maxn<<2];
void build_tree(int id,int l,int r){
if(l==r){
pos[myin[l]]=id;
return;
}
add_edge(id,lid);++du[lid];
add_edge(id,rid);++du[rid];
add_edge((n<<2)+lid,(n<<2)+id);++du[(n<<2)+id];
add_edge((n<<2)+rid,(n<<2)+id);++du[(n<<2)+id];
int mid=(l+r)>>1;
build_tree(lid,l,mid);
build_tree(rid,mid+1,r);
}
void update(int id,int l,int r,int x,int y,int p){
if(x>r || y<l) return;
if(x<=l && r<=y){
add_edge(p,id);++du[id];
add_edge((n<<2)+id,p);++du[p];
return;
}
int mid=(l+r)>>1;
update(lid,l,mid,x,y,p);
update(rid,mid+1,r,x,y,p);
}
void update1(int id,int l,int r,int x,int y,int p){
if(x>r || y<l || x>y) return;
if(x<=l && r<=y){
add_edge(p,id);
++du[id];
return;
}
int mid=(l+r)>>1;
update1(lid,l,mid,x,y,p);
update1(rid,mid+1,r,x,y,p);
}
void update2(int id,int l,int r,int x,int y,int p){
if(x>r || y<l || x>y) return;
if(x<=l && r<=y){
add_edge((n<<2)+id,p);
++du[p];
return;
}
int mid=(l+r)>>1;
update2(lid,l,mid,x,y,p);
update2(rid,mid+1,r,x,y,p);
}
#undef lid
#undef rid
}
il void dfs1(int now,int fa){
myf[now]=fa;
dep[now]=dep[fa]+1;
sonum[now]=1;
for(int to:E[now]){
if(to==fa) continue;
dfs1(to,now);
sonum[now]+=sonum[to];
if(sonum[hson[now]]<sonum[to]) hson[now]=to;
}
}
il void dfs2(int now,int topp){
top[now]=topp;
in[now]=++tim;
myin[tim]=now;
if(!hson[now]) return;
dfs2(hson[now],topp);
for(int to:E[now]){
if(to!=myf[now] && to!=hson[now]) dfs2(to,to);
}
}
il void update(int u,int v,int id){
add_edge(n*8+id,(n<<2)+pos[u]);++du[(n<<2)+pos[u]];
add_edge(pos[v],n*8+id);++du[n*8+id];
int x=u,fx=top[x],y=v,fy=top[y];
while(fx!=fy){
if(dep[fx]>dep[fy]) swap(fx,fy),swap(x,y);
if(y!=u && y!=v) SegementTree::update(1,1,n,in[fy],in[y],8*n+id);
else{
SegementTree::update(1,1,n,in[fy],in[y]-1,8*n+id);
if(y==u) add_edge(8*n+id,pos[u]),++du[pos[u]];
else add_edge(4*n+pos[v],8*n+id),++du[8*n+id];
}
y=myf[top[y]],fy=top[y];
}
if(dep[x]>dep[y]) swap(x,y);
if(x!=v && y!=v) SegementTree::update1(1,1,n,in[x],in[y],8*n+id);
else if(x!=y){
if(x==v) SegementTree::update1(1,1,n,in[x]+1,in[y],8*n+id);
else SegementTree::update1(1,1,n,in[x],in[y]-1,8*n+id);
}
if(x!=u && y!=u) SegementTree::update2(1,1,n,in[x],in[y],8*n+id);
else if(x!=y){
if(x==u) SegementTree::update2(1,1,n,in[x]+1,in[y],8*n+id);
else SegementTree::update2(1,1,n,in[x],in[y]-1,8*n+id);
}
}
queue<int> q;
il void inttopo(){
for(int i=1;i<=n*8+m;++i){
if(du[i]==0) q.push(i);
}
while(!q.empty()){
int u=q.front();
q.pop();
for(rg i=head[u];i;i=e[i].next){
int to=e[i].v;
--du[to];
if(du[to]==0) q.push(to);
}
}
}
il void clear(){
tim=0;
t=0;
for(rg i=1;i<=n;++i) <% myf[i]=dep[i]=sonum[i]=hson[i]=in[i]=myin[i]=top[i]=0;E[i].clear(); %>
for(rg i=1;i<=n*8+m;++i) head[i]=du[i]=0;
}
il void input(){
n=io::read();
int u,v;
for(rg i=1;i<=n-1;++i){
u=io::read(),v=io::read();
E[u].push_back(v);
E[v].push_back(u);
}
}
int main(){
// freopen("prison.in","r",stdin);
// freopen("prison.out","w",stdout);
T=io::read();
while(T--){
input();
dfs1(1,0);
dfs2(1,1);
SegementTree::build_tree(1,1,n);
m=io::read();
int s,t;
for(rg i=1;i<=m;++i){
scanf("%d %d",&s,&t);
update(s,t,i);
}
// for(rg i=1;i<=n*8+m;++i){
// cout<<i<<' '<<du[i]<<endl;
// }
inttopo();
bool mj=true;
for(int i=1;i<=8*n+m;++i){
if(du[i]) <% mj=false;break; %>
}
if(mj) printf("Yes\n");
else printf("No\n");
clear();
}
return 0;
}
/*
1
8
1 2
2 3
3 4
4 5
5 6
6 7
7 8
4
1 5
2 6
3 7
4 8
*/
倍增优化建图
对于这个,我们通过一道题来讲吧。
例题
【XR-1】逛森林
题目背景
NaCly_Fish 和 PinkRabbit 是好朋友。
有一天她去森林里游玩,回去跟 PinkRabbit 说:“我发现好多棵会动的树耶!”
PinkRabbit 动了动一只兔耳朵:“这有什么好稀奇的,我用一只兔耳朵就能维护每棵树的形态。”
NaCly_Fish 不服:“不止这样,我还看到有一些传送门,能从一条树枝跳到另一条树枝上呢!”
PinkRabbit 动了动另一只兔耳朵:“这有什么好稀奇的,我用两只兔耳朵就能统计每个传送门的信息。”

于是 NaCly_Fish 很郁闷,她向你求助,请帮帮她吧。
什么?你不愿意帮?
那她就不给你这题的分了。
题目描述
给你 \(n\) 个节点的森林,初始没有边。
有 \(m\) 个操作,分为两种:
\(1\ u_1\ v_1\ u_2\ v_2\ w\):表示构建一个单向传送门,从 \(u_1 \rightarrow v_1\) 简单路径上的所有节点,可以花费 \(w\) 的代价,到达 \(u_2 \rightarrow v_2\) 简单路径上的所有节点。若 \(u_1\) 到 \(v_1\) 或 \(u_2\) 到 \(v_2\) 不连通(由 \(2\) 操作产生的边不连通),则忽略此次操作。
\(2\ u\ v\ w\):表示将 \(u\) 和 \(v\) 节点间连一条花费为 \(w\) 的无向边,若 \(u\) 和 \(v\) 之间已连通(由 \(2\) 操作产生的边连通)则忽略此次操作。
经过这 \(m\) 次操作后,请你求出从 \(s\) 节点出发,到每个节点的最小花费。
输入格式
第一行三个正整数 \(n, m, s\),分别表示树的节点数、操作数、和起始节点。
接下来 \(m\) 行,每行若干个正整数,表示一次操作。
输出格式
输出一行 \(n\) 个整数,第 \(i\) 个整数表示从 \(s\) 节点出发,到 \(i\) 节点的最小花费。特别地,若不能到达\(i\)节点,则输出 -1。
样例 #1
样例输入 #1
9 11 5
2 2 1 2
2 3 1 5
2 4 2 10
2 5 3 9
2 6 5 3
2 7 6 6
2 8 7 2
2 9 4 2
1 1 1 4 9 2
1 8 5 1 6 1
1 3 6 9 6 1
样例输出 #1
1 1 1 1 0 1 7 9 1
提示
【样例说明】
这是样例中给出的树(严格来讲,这棵树也是一条链):
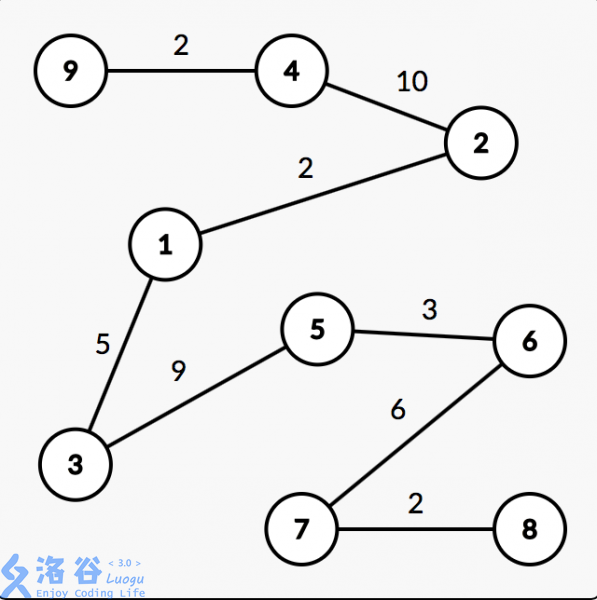
有三个传送门,其中两个是这样的:
- 从 \(1\) 号点可以花费 \(2\) 的代价到达 \(4 \rightarrow 9\) 简单路径上的所有节点(即 \(4, 9\) 号点)。
- 从 \(8 \rightarrow 5\) 简单路径上的所有节点(即 \(8, 7, 6, 5\) 号点)可以花费 \(1\) 的代价到达 \(1 \rightarrow 6\) 简单路径上的所有节点(即 \(1, 3, 5, 6\) 号点)。
容易看出从 \(5\) 号节点出发,到达其它节点的最小花费分别为:\(1, 1, 1, 1, 0, 1, 7, 9, 1\)。
【数据规模与约定】
对于第 \(1, 2\) 个测试点,\(1 \le n \le 100\),\(1 \le m \le 300\)。
对于第 \(3, 4\) 个测试点,\(1 \le n \le 1000\),\(1 \le m \le 3000\)。
对于 \(100\%\) 的数据,\(1\le n \le 50000\),\(1\le m \le 10^6\),\(1\le u,v \le n\),\(1\le w \le 100\)。
对于第 \(1\) ~ \(10\) 个测试点,每个 \(5\) 分。
对于第 \(11, 12\) 个测试点,每个 \(25\) 分。
解题:
题意概括:
有两个操作:
-
操作 \(1\):在连通的区间 \([u_1,v_1]\) 和连通的区间 \([u_2,v_2]\) 两个区间之间连一条权值为 \(w\) 的边(若区间不连通,忽略操作)。
-
操作 \(2\):若 \(u,v\) 之间没有连通,连一条权值为 \(w\) 的无向边。
求 \(m\) 次操作后,从节点 \(s\) 出发,到达每个节点的最小花费。
这道题,我们求的是 \(m\) 次操作后的结果,所以可以离线,也就是先把操作 \(2\) 的边连上。
而如何判断连通性呢?我们可以选择并查集。对于合法的操作 \(1\) 存起来,合法的操作 \(2\) 加边。
这是本题的特别之处,而剩下的,就是对操作 \(1\) 进行愉快的倍增优化建图了。