Regularization 正则化

课件翻译

Modeling Nonlinear Relation 非线性关系建模

• 上节课学了线性模型但是非线性模型也很重要

• 考虑一个由基函数的线性组合定义的模型

  在数学中，基函数是函数空间中特定基底的元素。 函数空间中的每个连续函数可以表示为基函数的线性组合，就像向量空间中的每个向量可以表示为基向量的线性组合一样。

  \[f(\boldsymbol{x}) = \beta_1\phi_1(\boldsymbol{x})+\beta_2\phi_2(\boldsymbol{x})+\cdots+\beta_p\phi_p(\boldsymbol{x}) \]

  其中 \(\phi_i(\boldsymbol{x})\) 是一个预定义的基函数

• 如果 \(\phi_i(\boldsymbol{x})\) 是非线性映射， \(f(\boldsymbol{x})\) 成为关于 \(\boldsymbol{x}\) 的非线性函数

例子

多项式模型： \( \phi_{1}(x)=x, \phi_{2}(x)=x^{2}, \phi_{3}(x)=x^{3}\)

是关于 \(x\) 的三次函数

Basis Function Regression 基函数回归

• 另一方面， \(f(\boldsymbol{x})\) 仍然是一个关于 \(\beta\) 的线性函数

  \[f(x)=\begin{bmatrix} \phi_1(\boldsymbol{x})&\cdots&\phi_p(\boldsymbol{x}) \end{bmatrix} \begin{bmatrix} \beta_1\\ \vdots \\ \beta_p \end{bmatrix} \]

  其中 \(\begin{bmatrix} \phi_1(\boldsymbol{x})&\cdots&\phi_p(\boldsymbol{x}) \end{bmatrix}\) 是特征，由此LSE可直接应用于估计 \(\beta\)

• 定义

  \[\boldsymbol{\phi} = \begin{bmatrix} \phi_1(x_1) & \phi_2(x_1) & \cdots & \phi_p(x_1)\\ \vdots & \vdots & &\vdots \\ \phi_1(x_n) & \phi_2(x_n) & \cdots & \phi_p(x_n)\\ \end{bmatrix} \]

  之后，对于 \(\beta\) 的LSE就可以写为

  \[\hat{\beta} = (\boldsymbol{\phi}^{\top}\boldsymbol{\phi})^{-1}\boldsymbol{\phi}^{\top}\boldsymbol{y} \]

Gaussian Basis Function 高斯基函数（径向基函数）

• 高斯径向基函数经常使用
  \[\phi_i(\boldsymbol{x})=\exp(-\frac{\left \| \boldsymbol{x}-\boldsymbol{c}_i \right \|^2 }{2\vartheta ^2} ) \]
  其中 \(\boldsymbol{c}_i\) 是一个预定义的中心参数， $\left | \boldsymbol{x}-\boldsymbol{c}_i \right |^2 $ 任意一点 \(\boldsymbol{x}\) 到某一中心点 \(\boldsymbol{c}_i\) 之间的欧式距离（L2范数） \(\vartheta\) 为宽度参数

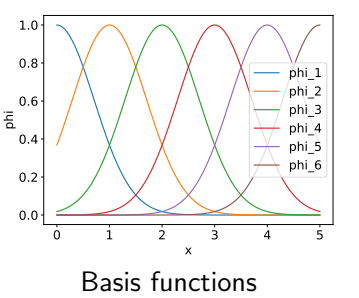
• 有6个基函数的示例

  \[\begin{aligned} \phi_{1}(\boldsymbol{x})= & \exp \left(-\|\boldsymbol{x}-0\|^{2}\right) \\ \phi_{2}(\boldsymbol{\boldsymbol{x}})= & \exp \left(-\|\boldsymbol{\boldsymbol{x}}-1\|^{2}\right) \\ & \vdots \\ \phi_{6}(\boldsymbol{x})= & \exp \left(-\|\boldsymbol{x}-5\|^{2}\right) \end{aligned} \]

  

Over-fitting 过拟合

• 非线性变换可能具有很高的灵活性，但有时结果会变得过于复杂，即过度拟合

  

  empirical feature map: 经验特征图

• 这个例子的训练误差为0，但显然预测性能较差

Ridge Regression 岭回归

详细可看机器学习算法实践-岭回归和LASSO

• 引入对 \(\beta\) 的惩罚机制

  \[\min_{\beta}\left \| \boldsymbol{y}-\boldsymbol{X}\beta \right \|^2+\lambda \left \| \beta \right \| ^2 \]

  \(\lambda>0\) 的时候为正则系数

  • 今后用 \(\boldsymbol{X}\) 代替 \(\boldsymbol{\phi}\)
  • 对 \(\beta\) 的惩罚机制抑制了所得模型的灵活性
  • 当 \(\lambda=0\) 时，岭回归被简化为LSE

• 通过求导

  \[\hat{\beta}_{ridge} = (\boldsymbol{X}^{\top}\boldsymbol{X}+\lambda\boldsymbol{I})^{-1}\boldsymbol{X}^{\top}\boldsymbol{y} \]

例子

• 和过拟合的例子一样的设置

  

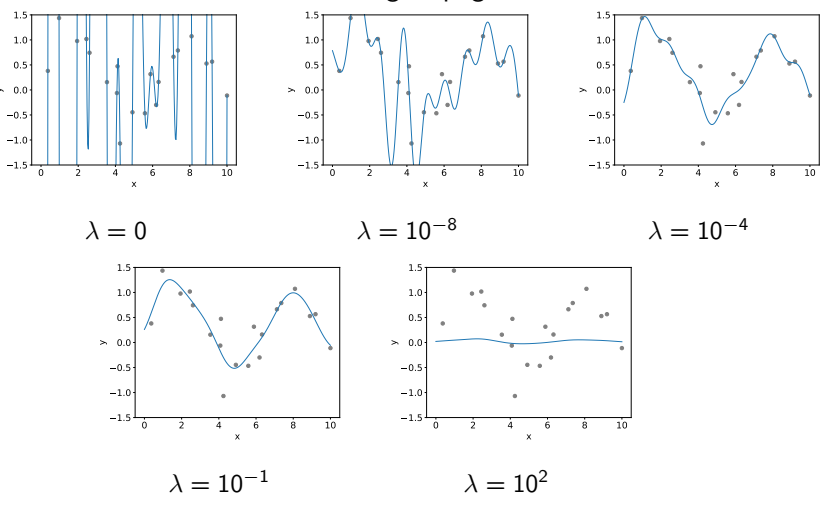
• 在实践中，应适当选择 \(λ\)（例如，通过使用交叉验证）

Regularization 正则化

• 通常，在参数上引入惩罚机制也被称为正则化，并广泛用于各种机器学习算法
• 正则化的有效性可以通过估计偏差和方差之间的权衡从理论上解释

Bias of Ridge Regression 岭回归的偏差

• 假设 \(\boldsymbol{y}=\boldsymbol{X} \boldsymbol{\beta}+\varepsilon\) ，其中 \(\beta\) 是未知的真实参数， \(\varepsilon \sim \mathcal{N}\left(\mathbf{0}, \sigma^{2} \boldsymbol{I}\right)\) 并且 \(\boldsymbol{X}^{\top}\boldsymbol{X}\) 可逆

• 岭回归是有偏估计（证明见附录）

  \[\begin{aligned} \mathbb{E}\left[\hat{\boldsymbol{\beta}}_{\text {ridge }}\right] & = \mathbb{E}\left[\left(\boldsymbol{X}^{\top} \boldsymbol{X}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{X}^{\top} \boldsymbol{y}\right]\\ & = \beta-\lambda(\boldsymbol{X}^{\top} \boldsymbol{X}+\lambda \boldsymbol{I})^{-1}\beta \end{aligned} \]

  其中 \(\lambda(\boldsymbol{X}^{\top} \boldsymbol{X}+\lambda \boldsymbol{I})^{-1}\beta\) 为偏差

• 两种极端情况

  • 如果 \(λ=0\) ，偏差变为0（因为那时，岭回归等效于LSE）
  • 如果 \(λ→ ∞\) ，偏差为 \(β\) （如果惩罚非常强，则得到的参数始终为0）

Variance of Ridge Regression 岭回归方差

• 岭估计量的方差为

  \[\begin{aligned} \mathbb{V}\left[\hat{\boldsymbol{\beta}}_{\text {ridge }}\right] & = \mathbb{V}\left[\left(\boldsymbol{X}^{\top} \boldsymbol{X}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{X}^{\top} \boldsymbol{y}\right]\\ & = \vartheta ^2\left(\boldsymbol{X}^{\top} \boldsymbol{X}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{X}^{\top} \boldsymbol{X}\left(\boldsymbol{X}^{\top} \boldsymbol{X}+\lambda \boldsymbol{I}\right)^{-1} \end{aligned} \]

  证明和LSE差不多一样

• 当 \(\lambda\) 越大方差越小

• 这表明岭回归可以减少估计方差，同时失去无偏性

Analyzing Prediction Error 分析预测误差

• 考虑给定测试点 \(x_{te}\) 的误差与真值的比较

  \[E(\hat{\boldsymbol{\beta}})=\left(\boldsymbol{x}_{\mathrm{te}}^{\top} \boldsymbol{\beta}-\boldsymbol{x}_{\mathrm{te}}^{\top} \hat{\boldsymbol{\beta}}\right)^{2} \]

• 由于 \(\hat{\beta}\) 取决于 \(y\) （正如我们在上一节课中看到的那样， \(y\) 是一个随机变量），我们考虑期望

  \[\mathbb{E}[E(\hat{\boldsymbol{\beta}})]=\mathbb{E}\left[\left(\boldsymbol{x}_{\mathrm{te}}^{\top} \boldsymbol{\beta}-\boldsymbol{x}_{\mathrm{te}}^{\top} \hat{\boldsymbol{\beta}}\right)^{2}\right] \]

Bias-Variance Decomposition 偏差-方差分解

• \(\mathbb{E}[E(\hat{\boldsymbol{\beta}})]\) 可以分解为（证明见附录）

其中 \((\boldsymbol{\beta}-\mathbb{E}[\hat{\boldsymbol{\beta}}])\) 是偏差， \(\mathbb{V}[\hat{\boldsymbol{\beta}}]\) 是方差

• 因此，因此，偏差-方差权衡与第一项和第二项的平衡有关

正则化

尝试通过减少方差来减少（预期的）预测误差，同时牺牲偏差

• 通常，当模型具有较高的灵活性时，估计方差往往较大

附录

岭回归的偏差

特征值分解

分解 \(\boldsymbol{X}^{\top} \boldsymbol{X}\) 的特征值

其中 \(\boldsymbol{U}\) 是正交矩阵 \(\left(\boldsymbol{U}^{\top} \boldsymbol{U}=\boldsymbol{U} \boldsymbol{U}^{\top}=\boldsymbol{I}\right)\) ，并且 \(\boldsymbol{\Lambda}\) 是在对角元素上具有本征值的对角矩阵

然后

注意对于非奇异矩阵 \(\boldsymbol{A}\) 和 \(\boldsymbol{B}\) ， \((\boldsymbol{A} B)^{-1}=\boldsymbol{A}^{-1} \boldsymbol{B}^{-1}\)

偏差-方差分解

习题

Exercise 0: Short Quiz

关于岭回归中 \(λ\) 的设置，下表中的四个空白单元格选择“Small”或“Large”

||Small \(λ\) |Large \(λ\) |

Exercise 1

• 使 \(\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{n}\) 成为具有一维输入的训练数据集

  \(x_{i}\)	\(y_{i}\)
  -2	-1
  -1	-2
  1	1
  2	3
  3	3

• 使 \(f\left(x_{i}\right)=\beta_{\text {ridge }} x_{i}\) （即，模型只有一个斜率参数）计算当 \(λ=1\) 和 \(λ=11\) 的时候的 \(\hat{\beta}_{\text {ridge }}\)

  \[\begin{aligned} \hat{\beta}_{ridge} & = (\boldsymbol{X}^{\top}\boldsymbol{X}+\lambda\boldsymbol{I})^{-1}\boldsymbol{X}^{\top}\boldsymbol{y}\\ & = (\begin{bmatrix} x_1 & \cdots & x_n \end{bmatrix} \begin{bmatrix} x_1 \\ \vdots\\ x_n \end{bmatrix}+\lambda )^{-1}\begin{bmatrix} x_1 & \cdots & x_n \end{bmatrix} \begin{bmatrix} y_1 \\ \vdots\\ y_n \end{bmatrix}\\ & = \frac{\sum_{i=1}^{n}x_iy_i }{\sum_{i=1}^{n}x_i^2+\lambda } \end{aligned} \]

  \(\lambda=1\) 时

  \[\hat{\beta}_{ridge} =\frac{2+2+1+6+9}{2^2+(-1)^2+1^2+2^2+3^2+\lambda}=1 \]

  \(\lambda=11\) 时

  \[\hat{\beta}_{ridge} =\frac{2+2+1+6+9}{2^2+(-1)^2+1^2+2^2+3^2+\lambda}=\frac{2}{3} \]

Exercise 2

对于Exercise 1中的数据集，计算估计偏差和方差，并填写下表的空白部分。

注意 \(\mathbb{E}\left[\hat{\boldsymbol{\beta}}_{\text {ridge }}\right]\) 应该是关于 \(\beta\) 的函数， \(\mathbb{V}\left[\hat{\boldsymbol{\beta}}_{\text {ridge }}\right]\) 应该是关于 \(\vartheta ^2\) 的函数

\(\lambda=1\) 时

\(\lambda=11\) 时

\(\lambda=1\) 时

\(\lambda=11\) 时

本栏目推荐文章
• Jmeter 如何连接mysql数据库？
• SQL Server 检测是不是数字型数据的两种方法
• 如何通过Navicat把MySQL远程数据库导入到本地数据库
• 和利时MACS6通过dat文件实现任意时间范围与测点的历史数据提取与科研分析
• 深入理解spring框架：剖析多线程模式下数据库连接
• 数据可视化是如何帮助大型企业提高效率的？
• 用jacoco统计JAVA项目测试代码覆盖率
• redis 数据库
• openpyxl模块--------------------------------重复数据
• Django客户端应用1向服务端应用2发送POST请求并接收解析数据

专论 正则 Regularization 统计数据 数据专论 正则regularization统计数据 专论 线性 统计数据revisiting 正则regularization方法 神经网络 正则regularization神经 正则 编码器regularization recommendation 正则regularization normalization 正则regularization线性 函数 神经网络 正则regularization overfitting 正则 表达式 数据 正则 数据