很有意义很有思维量的图论题。(摸了好久做出来了,很有感觉)
本文的「环」均指简单环,「路径」均指简单路径。
初步
考虑这个「存在一条三种颜色的路径」这个限制其实是很弱的,首先的感觉就是我们随便画出一些连通图,随便选择三条边,基本都能找到一条经过这三条边的路径。
于是我们考虑将难以描述的弱限制单步容斥成相反的强性质:考虑存在三种颜色但不存在一条三色路径的染色计数。这显然一个限制更加明确的问题。
特殊情况
让我们先来考虑从特例分析:树。
如果存在三种颜色的边且无法在树上被一条简单路径所连接,考虑任意两条颜色不同的边:

其路径上不可能存在第三种颜色的边,且如果某个位置要存在第三种颜色的边,则这条边到到这条路径上的那个点两侧必须全是不同的颜色,否则从第三种颜色的边走到该路径,然后经过其它两种颜色的点。而且第三种颜色的边到该路径上仅能存在该颜色,否则到了直接选择没有的那侧就有三种颜色了。
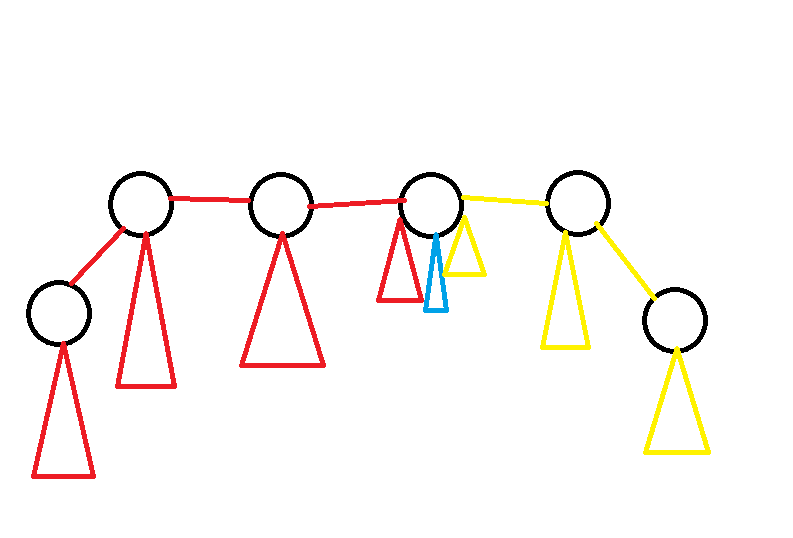
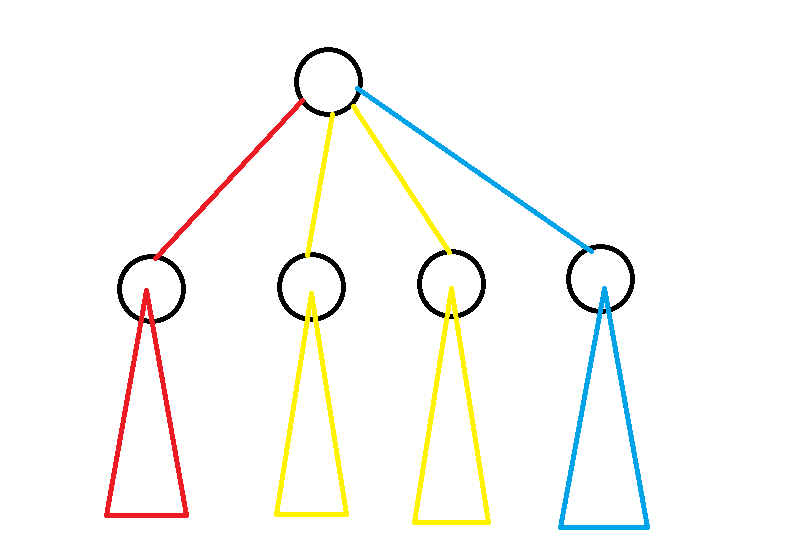
所以我们得到,树的染色方案的形态一定如下图,即存在一个点使得其每个子树内颜色全相同(其实我觉得这个很显然不需要分析啊)。
于是枚举这个点,方案数即将子树染色且每种颜色都出现的方案数 \(\sum f(deg_i)\),简单容斥可以得到\(f(x)=x^3-3x^2+3\)。
泛化
树上的问题向图上的问题拓展的一步就是考虑环,首先我们来考虑一个特定的环的情况,环上可能有一种/两种/三种颜色。
首先如果一个长度大于 \(4\) 的环上有三种颜色,那么至少一种颜色出现了两次,考虑指定一条该颜色边不用然后选择其他边即存在了三色路径,所以不存在长度 \(\geq 4\) 的有三种颜色的环。
考虑存在一个三色的三元环,如果一个点 \(\text{P}\) 上有向外连的边,则这些边只能和点在环上相对的边是同色的,如下:
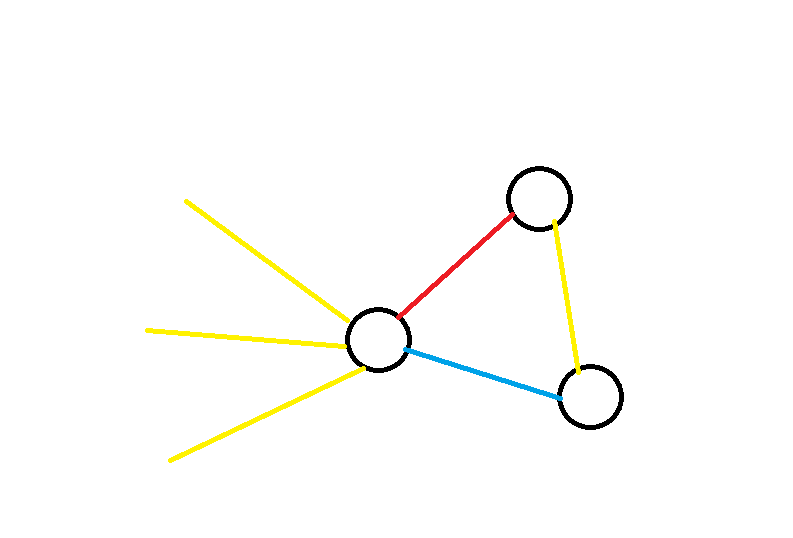
因为如果连接了颜色和邻边相同的边 \(\text{E}\) ,则可以选择一条路径 \(\text{E} \to \text{P 和 E 颜色不同的邻边}\to \text{P 的对边}\) 同时拥有三种颜色,所以一个点上只能连出和对边颜色相同的边。
如果这个三元环上有两个点同时向外连向了外界不同的两个点,那么一定也会出现三色路径(显然从这某个点进入然后走环上这条边进入其它点离开就是一条三色路径),下面这种情况是不能出现的。
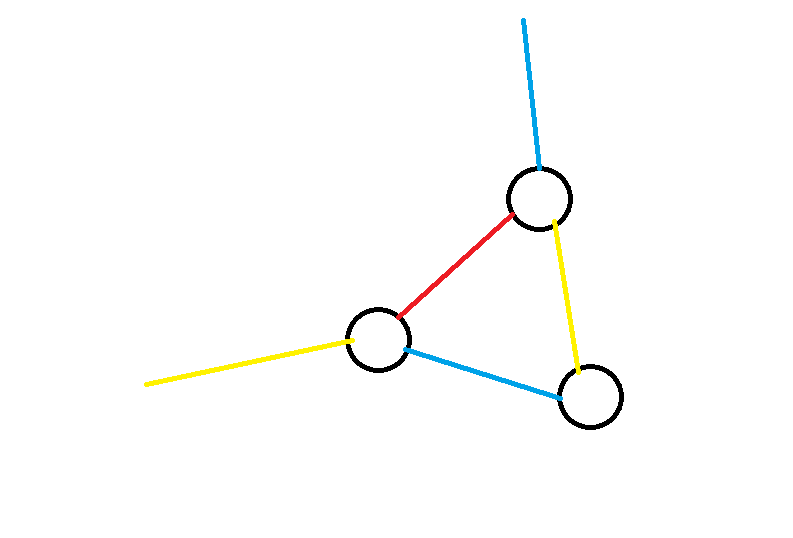
所以说,三色三元环出现有且仅有以下两种情况:
- 有至多一个点向外连边,且外面的所有边颜色都和三元环上的对边相同。
- 有且仅有两/三个向外的同一个点连了边。
第一种情况是好处理的,直接枚举这种 \(O(n)\) 条两端点度数均为 \(2\) 的点并判断是否为这种三元环,如果是则会增加 \(3!=6\) 种颜色方案(确定完环上的边外面的边也确定了),然后直接做就完了。
让我们继续考虑第二种情况,并继续考虑这个环外的 \(\text{T}\) 连边情况:
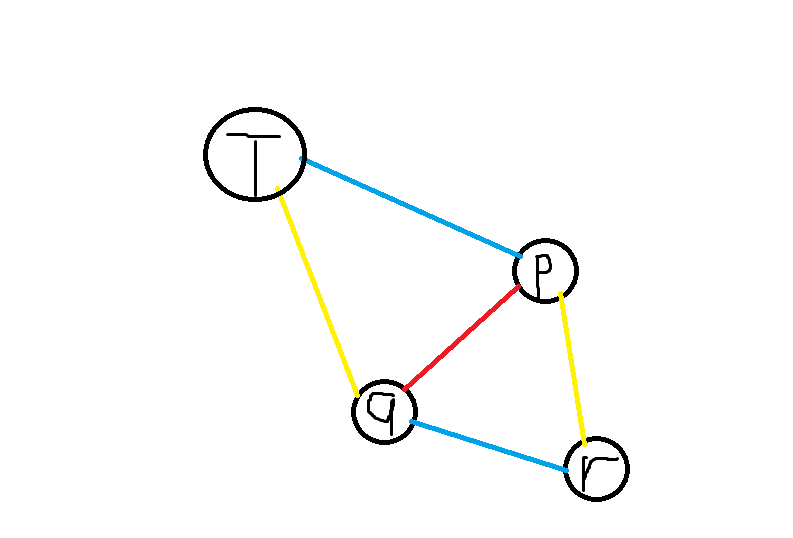
这个点 \(\text{T}\) 已经有了 \(\text{P}\to\text{Q}\to \text{T}\), \(\text{Q}\to\text{P}\to \text{T}\), \(\text{R}\to\text{P}\to \text{T}\),这三条路径,分别限制该点不能再向外连边了。所以这个点不可能再向外连接任何其他边,环上其它点也不可以向任何其它点连边(如果练了就同时向外连向了外界不同的两个点),所以不可以再有其它点了,所以这种情况的出现仅当 \(n\leq 4\),当 \(n\leq 4\) 时可以选择手动判掉或者枚举颜色。
所以我们处理完了存在三色环的情况,所以我们接下来可以把限制加强到「环上不存在三种颜色」的问题并继续考虑下去。
加强限制
考虑环上存在两种颜色的情况:
考虑第三种颜色的边连接的点 \(\text{P}\),我们只需要找到一条以 \(\text{P}\) 为终点且同时拥有两种颜色的路径即可走到 \(\text{P}\) 并走到第三种颜色了。
考虑 \(\text{P}\) 两侧的边,因为环的大小 \(\geq 3\),这时候一定有一种颜色在环上出现了至少两次,考虑选择该颜色的一条与 \(\text{P}\) 相邻的边不选,环上剩余的边构成了一条以 \(P\) 为端点的有两种颜色的路径,所以一定存在三色路径。
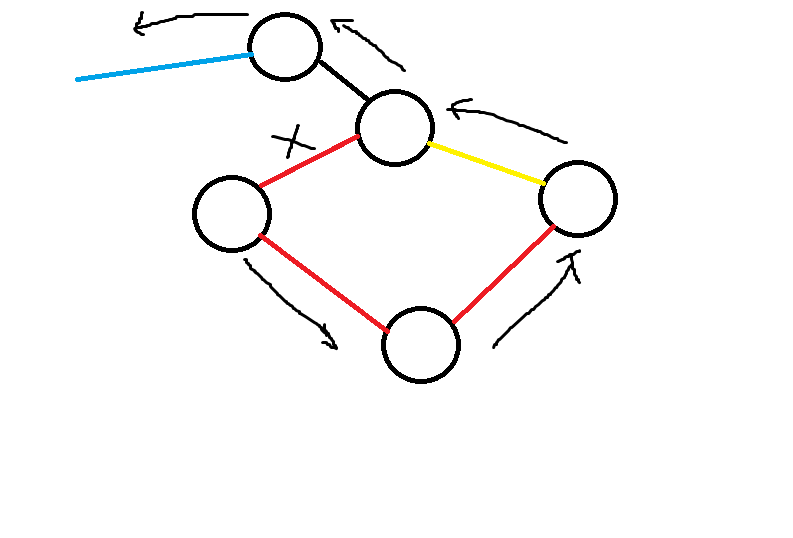
所以得到环上不能存在两种颜色,于是我们现在就得到了一个很强的限制「一个环上的边必须是同一种颜色」,这也意味着一个点双连通分量内的所有边的颜色都相同。
最终问题
问题到现在已经有了「一个点双连通分量内的边颜色全相同」这样的强限制,考虑建出圆方树,接下来问题变成了「将方点染色,不存在一条简单路径使得经过三种颜色的方点」,几乎和树上问题一模一样,我们同样可以和树上问题相同地得出结论:最终染色方案的形态一定存在一个圆点,使得其每个子树内方点颜色全相同,答案即 \(\sum f(deg_i)\),其中 \(deg_i\) 表示圆点 \(i\) 在圆方树上的度数。
问题至此已经解决,每部分的时间复杂度都是 \(O(n+m)\)。
回顾整个过程,我们首先将若限制转化为对称的强限制,很多「大多数情况都存在」类的问题都可以通过容斥或单步容斥变成「不存在」,会方便很多,接下来逐步将一个限制通过分析某种较弱的特殊情况,并单独考虑这种情况,解决这种问题后将「不存在这样的结构」当作限制解决接下来的问题。