双指针
也常叫 \(two-pointers\) ,是一种简单又灵活的技巧和思想,单独使用可以轻松解决一些特定问题,和其他算法结合也能发挥多样的用处。
顾名思义,就是同时使用两个指针,在序列、链表结构上指向的是特定位置,在树、图上指向的是节点,通过同向移动,或者相向移动来维护、统计信息。
例题
给定一个存在环的单向链表,需要找出环的大小和环的起点
\(solution\) :首先两个指针只想链表的头部,令一个指针一次走一步,另一个指针一次走两步,如果他们相遇,证明有环,否则无环
显而易见,相遇的时候慢指针走过的步数就是环的长度的整数倍。

利用这个等式,可以在两个指针相遇后,将其中一个指针一道表头,让两者都一步一步走,再度相遇的位置即为环的起点。
大小的话相遇之后再跑一圈就可以了
双向搜索
双向同时搜索:基本思路是从状态图上的起点和终点同事开始进行广搜或者深搜,如果发现搜索的两端相遇了,那么可以认为是获得了可行解
Meet in the middle:主要思想是将整个搜索过程分成两半,分别搜索,最后将两半的结果合并。经过这个算法可以将复杂度的指数减半,也就是减少了搜索的深度。
例题 P1429 平面最近点对
给定平面上n个点,找出其中一对点对的距离,使得在这n个点的所有点对中,该距离为所有点对中最小的,其中\(n \le 10^5\)
\(solution\)
先将所有点按照x坐标排序。考虑分治。先递归计算两个大小相同的子区间,分别得到两个答案,设 \(d = \min(d1,d2)\) ,考察跨过中线的点对

对于1区间中的某个点,2区域中可供他选择的范围是一个\(d \times 2d\) 的矩形,由于2区间中两点的间距必然不小于 \(d\) ,故至多有六个待选点
故对区域内点按照 y 坐标归并排序,在归并排序的过程中,就可以线性扫描计算这部分贡献。
int n;
pii w[N];
double dis(int i,int j) {
double dx = w[i].fi - w[j].fi;
double dy = w[i].se - w[j].se;
return sqrt(dx * dx + dy * dy);
}
double get(int l,int r) {
if (l >= r) return dinf;
int mid = (l + r) >> 1;
double d = min(get(l,mid),get(mid + 1,r));
for (int i = mid; i >= l; i --) {
if (w[mid + 1].fi - w[i].fi >= d) break;
for (int j = mid + 1; j <= r; j ++) {
if (w[j].fi - w[i].fi >= d) break;
d = min(d,dis(i,j));
}
}
return d;
}
int main(){
n = fr();
for (int i = 1; i <= n; i ++) {
w[i].fi = fr();
w[i].se = fr();
}
sort(w + 1,w + 1 + n);
double ans = get(1,n);
printf("%.4lf",ans);
return 0;
}
例题
2962 Lights G
因为 \(n \le 40\),所以可以想到用双向搜索, 搜索的时候就从初始状态(全 \(0\) )把所有前面一半可能的情况都跑一遍,然后再从终止状态(全 \(1\) )的时候dfs一遍,把后面的一半情况跑了。
然后在前面跑的时候记录一下到这个点要经过多少次变化,后面一次跑的时候如果碰到了和前面一样的情况,那么就代表着这两个状态合在一起可以点亮全部灯。然后再取一个 \(min\) 就可以了。
这里需要注意的一点就是,判断当前状态的时候要用 \(lwl\) 不然会超 \(int\) 变成负数。还有就是不能单纯的判断当前这个点所对应的 \(map\) 值是不是 \(0\) ,因为有可能后面一半操作就可以点亮所有的灯,所以特判一下。然后我这里是直接一开始赋值为 \(1\),后面再减。
int n,m;
vector<int> e[N];
map<lwl,int> dis;
int ans = inf;
void dfs1(int u,lwl t,int cnt) {
if (dis[t]) dis[t] = min(dis[t],cnt);
else dis[t] = cnt;
if (u > n / 2) return ;
dfs1(u + 1,t,cnt);
t ^= ((lwl)1 << (u - 1));
for (auto i : e[u]) {
t ^= ((lwl)1 << (i - 1));
}
dfs1(u + 1,t,cnt + 1);
}
void dfs2(int u,lwl t,int cnt) {
if (dis[t]) ans = min(ans,cnt + dis[t]);
if (u > n) return ;
if (ans <= cnt) return ;
dfs2(u + 1,t,cnt);
t ^= ((lwl)1 << (u - 1));
for (auto i : e[u]) {
t ^= ((lwl)1 << (i - 1));
}
dfs2(u + 1,t,cnt + 1);
}
int main(){
n = fr(),m = fr();
int a,b;
for (int i = 1; i <= m; i ++) {
a = fr(),b = fr();
e[a].push_back(b);
e[b].push_back(a);
}
dfs1(1,0,1);
dfs2(n / 2 + 1,((lwl)1 << n) - 1,0);
fw(ans - 1);
return 0;
}
3066 Running Away From the Barn G
这个题就是找一下自己到上面哪一个点的距离刚好比k大,然后这一段区间他都有一个1的贡献,用二分和树上差分就可以了。老师讲的是双指针,但是没有听懂。
int n;
lwl k;
int fa[N][20],de[N];
lwl w[N],dis[N];
int cf[N];
void get(int u) {
cf[u] ++;
lwl qwq = k;
for (int i = log2(de[u]); i >= 0; i --) {
if (dis[u] - dis[fa[u][i]] <= qwq) {
qwq -= dis[u] - dis[fa[u][i]];
u = fa[u][i];
}
}
cf[fa[u][0]] --;
}
int main(){
n = fr(),k = fr();
for (int i = 2; i <= n; i ++) {
fa[i][0] = fr();
w[i] = fr();
dis[i] = w[i] + dis[fa[i][0]];
}
for (int i = 1; i <= n; i ++) {
de[i] = de[fa[i][0]] + 1;
for (int k = 1; k <= log2(de[i]); k ++)
fa[i][k] = fa[fa[i][k - 1]][k - 1];
}
for (int i = 1; i <= n; i ++) {
get(i);
}
for (int i = n; i; i --) {
cf[fa[i][0]] += cf[i];
}
for (int i = 1; i <= n; i ++) {
fw(cf[i]);
ch;
}
return 0;
}
练习
今天的题有点难想,但是数据极弱,第二题 \(n^2\) 暴力就可以水过去,第三题直接 \(puts('0')\) 就有五十分。第一题不知道数据咋样,写的正解。
A.囊中羞涩
看题目范围 \(n \le 40\) 可以想到用双向搜索。
这个题就直接把前面一半的情况都处理一下,然后记录一下用一下前缀和,后面算的时候找到 \(m - money\) 对应的前面的情况再累加一下就可以了。
int n;
lwl m,idx;
lwl w[N];
set<lwl> s;
int sum[1 << 21];
lwl dy[1 << 21];
lwl ans;
map<lwl,int> cnt;
void dfs1(int u,lwl money,int flag) {
if (money > m) return ;
cnt[money] += flag;
s.insert(money);
if (u > n / 2) return ;
dfs1(u + 1,money,0);
money += w[u];
dfs1(u + 1,money,1);
}
void dfs2(int u,lwl money,int flag) {
if (flag) {
lwl l = 1, r = idx;
while (l <= r) {
lwl mid = (l + r) >> 1;
if (dy[mid] > m - money) r = mid - 1;
else l = mid + 1;
}
ans += sum[r];
}
if (u > n) return ;
dfs2(u + 1,money,0);
money += w[u];
dfs2(u + 1,money,1);
}
int main(){
n = fr();
m = fr();
for (int i = 1; i <= n; i ++) {
w[i] = fr();
}
cnt[0] = 1;
dfs1(1,0,0);
idx = 0;
for (auto i : s) {
dy[++ idx] = i;
}
for (int i = 1; i <= idx; i ++) {
sum[i] = sum[i - 1] + cnt[dy[i]];
}
dfs2(n / 2 + 1,0,1);
fw(ans);
return 0;
}
B.交换人生
这个序列如果前面一个端点定下来的话,是一个单调不减的序列,所以可以用二分找出。
因为如果这个数能给答案提供贡献,那么前面的异或值要有至少一位之前的异或值对应的是 \(0\) ,而这个数这一位对应的是 \(1\) 。
所以我们就枚举起点,然后这个起点所对应的最大值就是这个点到 \(n\) 这一段的答案,这个值是一样的。如果当前求出来的值比之前的 \(ans\) 要大,我们就二分找出这个值在这个序列里面对应的最小值,然后更新答案。
昨天搞第三题去了这题的代码没有写,就贴贴 \(xyzfrozen\) 的代码()
#define int long long
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
int get(int p)
{
int l=p,r=n,res=n;
while(l<=r)
{
int mid=(l+r)>>1;
if(s[mid]-s[p-1]-(d[mid]^d[p-1])>=ans) r=mid-1,res=mid;
else l=mid+1;
}
return res;
}
void solve()
{
ans=s[n]-d[n],L=1,R=n;
for(int i=1;i<=n;i++)
{
int val=s[n]-s[i-1]-(d[n]^d[i-1]);
if(val>ans) ans=val,L=i,R=get(i);
else if(val==ans)
{
int tR=get(i);
if(tR-i<R-L || (tR-i==R-L && i<L)) L=i,R=tR;
}
}
fw(L),pt,fw(R);
}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) a[i]=fr();
for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i],d[i]=d[i-1]^a[i];
solve();
return 0;
}
C.交换人生
原题 Loj353 花火
这一题正解真他妈难想。老师讲了两遍才懂。
首先观察这个序列,如果他没有交换任意两个元素的话,只交换相邻两个元素就是求逆序对的数量,如果交换两个元素的话,他提供的贡献就是减少了序列中逆序对的数量。
首先要考虑到这个交换在一开始交换或者其他时候交换其实提供的贡献是一样的。(如果中间交换其实可以先一开始交换再按照原来的方法交换,效果是一样的)。
考虑交换两个元素可以提供的贡献。设交换 \(w[i],w[j]\) \(i < j\) ,那么可以发现的是如果 \(w[i] < w[j]\) 的话是没有交换的必要的,所以我们要交换 \(w[i] > w[j]\) 的元素。如果交换这两个元素,其实对于这两个元素旁边的两个元素是没有影响的,那么考虑中间的元素。如果中间的元素同小于或者同大于这两个数,那么逆序对的数量是不会改变的,那么对于值在他们中间的数并且位置在他们中间的数,就可以减少两个逆序对。
然后我们就可以把这一题抽象到坐标系中,横坐标代表位置,纵坐标代表值。就如下图
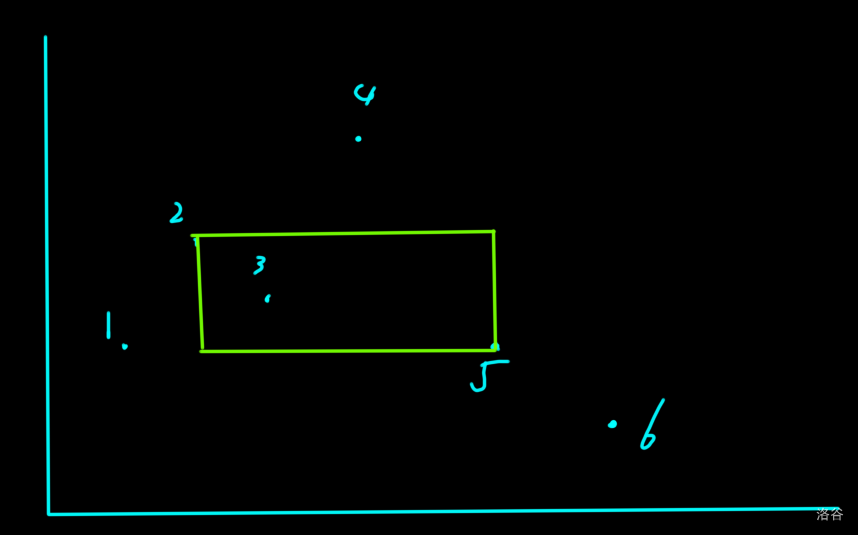
那么问题就抽象为了找到两个点并且以这两个点为左上和右下端点构造矩形,使其框住的点最多。
那么这个时候,我们先找到潜在的左上端点和右下端点,因为图中显然不管怎么选,6点作为右下端点一定优于5点作为右下端点,2点作为左上端点一定优于3点作为左上端点,所以这个时候我们用单调栈可以找出所有最优的左上端点和右下端点,处理出来的线差不多就是这个样子(下图蓝点):

然后我们考虑每一个点能给他们的贡献。观察图中的绿点,绿点可以给绿色括号中的上面三个蓝色点一个贡献,给下面三个蓝色点一个贡献,这个时候可以二分找出蓝色点的边界在哪里。
然后我们进一步抽象,可以再建立一个坐标系,横坐标是左上端点,纵坐标是右下端点,每一个这样的绿点其实在图中可以对应成一个矩形,我们要求的就是图中哪一个点被矩形覆盖的次数最多。这个时候就转化成了扫描线的问题。

扫描线的话就用线段树就可以了。就是给每一条边一个边权,左边的边给 \(1\) ,右边的边给 \(-1\),然后这样扫过去,线段树就维护一下区间最大值就可以了,具体看 \(ACwing248\) 窗内的星星。然后求一开始的逆序对的话用归并排序就可以了。最后求出来点最多的覆盖次数减的时候记得要乘二
// 线段树
struct node{
int maxn,laz;
}tr[N << 2];
// 扫描线
struct Node{
int l,r,h,w;
}line[N << 1];
int n,cnt;
int w[N],temp[N];
int ls[N],rx[N]; // 左上右下的点集
lwl get(int l,int r) {
if (l >= r) return 0;
int mid = (l + r) >> 1;
lwl ans = get(l,mid) + get(mid + 1,r);
int k = 0,i = l,j = mid + 1;
while (i <= mid && j <= r) {
if (w[i] < w[j]) temp[k ++] = w[i ++];
else {
temp[k ++] = w[j ++];
ans += (mid - i + 1);
}
}
while (i > mid && j <= r) temp[k ++] = w[j ++];
while (i <= mid && j > r) temp[k ++] = w[i ++];
for (int i = l, j = 0; i <= r; i ++, j ++) {
w[i] = temp[j];
}
return ans;
}
bool cmp(Node a,Node b) {
if (a.h == b.h) return a.l < b.l;
return a.h < b.h;
}
void pushup(int idx) {
tr[idx].maxn = max(tr[il].maxn,tr[ir].maxn) + tr[idx].laz;
}
void modify(int L,int R,int l,int r,int idx,int x) {
if (L > R) return ;
if (L >= l && R <= r) {
tr[idx].maxn += x;
tr[idx].laz += x;
return ;
}
int mid = (L + R) >> 1;
if (mid >= l) modify(L,mid,l,r,il,x);
if (mid < r) modify(mid + 1,R,l,r,ir,x);
tr[idx].maxn = max(tr[il].maxn,tr[ir].maxn) + tr[idx].laz;
}
int main(){
freopen("qwq.in","r",stdin);
n = fr();
for (int i = 1; i <= n; i ++) {
w[i] = fr();
}
ls[0] = -inf,rx[n + 1] = inf;
for (int i = 1; i <= n; i ++)
ls[i] = max(ls[i - 1],w[i]);
for (int i = n; i; i --)
rx[i] = min(rx[i + 1],w[i]);
for (int i = 1; i <= n; i ++) {
int l = lower_bound(ls + 1,ls + 1 + n,w[i]) - ls;
int r = lower_bound(rx + 1,rx + 1 + n,w[i]) - rx;
if (l >= i || r <= i) continue;
if (rx[r] > w[i]) r--;
line[++cnt] = {l,i - 1,i + 1,1};
line[++cnt] = {l,i - 1,r + 1,-1};
}
sort(line + 1,line + 1 + cnt,cmp);
lwl t = 0;
for (int i = 1; i <= cnt; i ++) {
modify(1,n,line[i].l,line[i].r,1,line[i].w);
t = max(t,tr[1].maxn);
}
lwl ans = 0;
ans = get(1,n);
fw(ans - t * 2);
return 0;
}