前言
出了一道题,给了 \(O((2n)!\text{poly}(n))\),\(O(\)A000670\([m]\text{poly}(n))\),\(O((1+\sqrt{5})^n\text{poly}(n))\),\(O(n^6)\),\(O(n^5)\),\(O(n^4),\)\(O(n^3)\) 的部分分,其中除了 \(O(n^4)\) 和 \(O(n^3)\) 都有针对性做法。但是只有 \(O((2n)!\text{poly}(n))\) 和 \(O(n^3)\) 有人写,其余人都写了比原标算简单的 \(O(n^2)\) 做法。
在此记录 \(3\) 种不同的做法,按照我理解的时间顺序从小到大标号。
题目描述
你有一个 \(n\times n\) 的网格。对于每个 \(1\le i\le n\),你在网格第 \(i\) 行的前 \(l_i\) 列摆上了花盆,并种下了种子。
现在你对每行每列都使用了一些魔法。对于第 \(i\) 行,假设你对行中的所有花盆施加了 \(x_i\) 点火魔法。对于第 \(j\) 列,假设你对列中的所有花盆施加了 \(y_j\) 点冰魔法。
对于一个花盆,假设它位于第 \(i\) 行第 \(j\) 列,那么 \(x_i>y_j\) 时会长出火焰花,否则会长出寒冰花。
问对于所有可能的 \(x_1,x_2,\cdots,x_n,y_1,y_2,\cdots,y_n\),共能生成多少种不同的花园。答案对 \(10^9+7\) 取模。
\(n\le 7500\)。
算法 3
考虑如下过程:维护一个序列 \(s\),初始为空,依次插入 \(y_1,y_2,\cdots,y_n\) 这些变量。在插入 \(y_{l_i}\) 以后,\(x_i\) 可以选定 \(s\) 的一个前缀,设它包含的变量集合为 \(A_i\),我们要计数有多少种可能的 \((A_1,A_2,\cdots,A_n)\)。
我们可以假设已经确定了 \((A_1,A_2,\cdots,A_n)\),考虑增加一个限制:每次插入 \(y_j\) 时,要把它插到当前 \(s\)(注意不是最终的 \(s\))中最靠右的可能位置。那么这个位置要么是 \(s\) 的末尾,要么必须 \(\exists i\),使得 \(l_i\ge j\),且 \(A_i\) 包含 \(y_j\) 但不包含当前 \(s\) 中 \(y_j\) 的后继。
我们依次考虑 \(y_1,y_2,\cdots,y_n\),在考虑完 \(y_{l_i}\) 后考虑 \(x_i\)。假设已经考虑了前 \(i\) 个变量,当前 \(s\) 中共有 \(k\) 条邻边需要等待“切断”,即之后的某个 \(A_i\) 必须包含左端点、不包含右端点。设 \(f_{i,k}\) 表示这种情况下已经确定的 \(A\) 和 \(s\) 共有多少种可能。最终状态 \(f_{2n,0}\) 中,一个方案 \((A_1,A_2,\cdots,A_n)\) 只会对应恰好一个 \(s\),但一个 \(s\) 可能对应多个方案。
在插入 \(y_j\) 时,插在末尾或插在某条边上都使 \(k\) 不变,否则会使 \(k\) 增加 \(1\)。在确定某个 \(A\) 时,卡在某条边上会让 \(k\) 减少 \(1\),否则 \(k\) 不变。
算法 2
观察到 \(l_i\) 的顺序不影响答案,不妨把 \(l\) 从小到大排序。
对于位置 \((i,j)\),我们把它是否满足 \(x_i>y_j\) 记作 \(\texttt{1}\) 或 \(\texttt{0}\)。
一个花园满足条件 \(\Leftrightarrow\) 下列两种子矩形均不出现(不一定是连续子矩形):
01 10
10 01
为了证明,我们要先建一个图:把 \(x_i,y_j\) 看作点,对于每个位置 \((i,j)\),若 \(x_i>y_j\) 则从 \(y_j\) 向 \(x_i\) 连边,否则反向连边。
\(\Rightarrow\):反证。如果出现某种子矩形,则存在一个长度为 \(4\) 的环,推出变量大于自身,矛盾。
\(\Leftarrow\):反证。若一个花园不满足条件,一定是存在了某个长度为 \(2k\) 的环。我们考虑环中 \(x\) 的顺序是 \(x_{p_1}<x_{p_2}<\cdots<x_{p_k}<x_{p_1}\),不妨设 \(p_1\) 最小。
pk 0
p2 1 ?
p1 0 1
考虑问号处填什么。如果填的是 \(\texttt{0}\) 则已经出现了不合法的子矩形。如果填的是 \(\texttt{1}\) 则图中 \(x_{p_k}\) 到 \(x_{p_2}\) 存在一条长度为 \(2\) 的路径(原来长度为 \(4\)),环长变为 \(2k-2\)。归纳,最终会使环长变为 \(4\),得到不合法的子矩形。
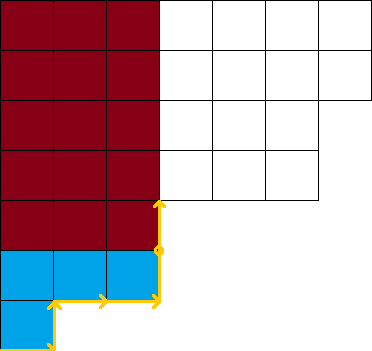
考虑沿着阶梯型轮廓进行 DP。令 \(f_{i,S}\) 表示当前处于轮廓的第 \(i\) 个点(图中的橙色圆点),若把红色区域的每行看作 \(\texttt{01}\) 串,当前 \(\texttt{01}\) 串的集合为 \(S\),这个状态下蓝色区域共有多少种填写方案。\(S\) 需要满足,一定存在一个其元素的排列 \(s_1,s_2,\cdots,s_k\),使得 \(\forall 1\le j<k\) 都满足 \(s_j \wedge s_{j+1} = s_j\)。否则就会出现不合法子矩形。可以观察到,如果 \(S\) 合法,那么元素的排列顺序是唯一的。
考虑在轮廓线上向右移动一步的转移,此时红色区域向右扩一格。我们可以选一个前缀的 \(s_i\) 在末尾_添加 \(\texttt{0}\),其余 \(s_i\) 在末尾添加 \(\texttt{1}\),这样使 \(|S'| = |S|\)。也可以选一个 \(s_i\),将其分别添加 \(\texttt{0}\) 和 \(\texttt{1}\) 成为 \(2\) 个新串,然后对于在它左边的串添加 \(\texttt{0}\),在它右边的串添加 \(\texttt{1}\),这样使 \(|S'|= |S|+1\)。
考虑在轮廓线上向上移动一步的转移,此时蓝色区域新加入一行。这一行可以填 \(|S|\) 种串,并且由于红色区域少了一行,\(S'\) 可能是 \(S\) 或者 \(S\) 去掉其中任意一个元素。
综上所述,\(f_{i,S}\) 的转移只和 \(|S|\) 有关,我们令 \(g_{i,k} = \sum_{S} [|S|=k]f_{i,S}\) 即可转移。
算法 1
考虑把所有 \(x_i,y_j\) 视作点,建立有向图。如果一个位置 \((i,j)\) 要求 \(x_i>y_j\),就从 \(y_j\) 向 \(x_i\) 连边,否则就从 \(x_i\) 向 \(y_j\) 连边。如果图中存在环,就一定可以推出某个变量大于自身,从而矛盾。否则,图是一个 DAG,此时我们可以按拓扑序给每个变量赋值。我们枚举拓扑序,得到一个 \(O((2n)!n^2)\) 的暴力。
考虑固定一个 DAG,观察拓扑排序的过程。我们把钦定 \(x_i>y_j\) 的格子称为白格,钦定 \(x_i\le y_j\) 的格子称为黑格。从而,一个花园合法当且仅当:每次能找到一个全白的列或一个全黑的行,将其删掉,在若干次后能把花园删空。
观察到 \(l_i\) 的顺序不影响答案,不妨设 \(l\) 单调不降。这样,我们只需关心花园的阶梯状轮廓。而且,无论是删去一行还是一列,轮廓仍然保持阶梯状。
对于一个轮廓 \(a\),考虑计算 \(2\) 个值:
- \(f(a)\) 表示花园个数。
- \(g(a)\) 表示不存在全白列的花园个数。
考虑 \(g(a)\)。这样的花园一定存在至少一个全黑行。考虑容斥,钦定一个行的非空子集是全黑的。假设其中最长的一行是 \(x_i\),那么对于所有满足 \(j>l_i\) 的列 \(y_j\),要再进行容斥,也就是钦定其中一个子集是全白的。最后,我们把钦定的行和列删除,递归到计算 \(f(a')\)。
考虑 \(f(a)\)。我们枚举全白列的集合,可以分为 \(2\) 种情况:
- 全白列为全集。即花园全白,有 \(1\) 种方案。
- 不为全集。此时可以删除这些列,递归到计算 \(g(a')\)。
第 \(2\) 种情况中,我们先是递归到 \(g(a')\),然后到 \(f(a'')\),设这 \(2\) 个过程分别为 \(p,q\)。假设在 \(q\) 中钦定的最长一行是 \(x_i\)。假设在 \(p,q\) 中被钦定的列的并集内,\(j\) 最大的列是 \(y_j\)。如果 \(j>l_i\),那么这列可能在 \(p\) 中被钦定(系数为 \(+1\)),也可能在 \(q\) 中被钦定(系数为 \(-1\)),对答案的贡献为 \(0\),故这种情况无需考虑。
因此,可以直接描述从 \(f(a)\) 递归到 \(f(a'')\) 的过程:
- 先钦定一个非空行子集,假设有 \(c\) 行,最长一行是 \(x_{\text{max}}\),最短一行是 \(x_{\text{min}}\)。
- 然后钦定一个列子集,只能在 \(1\sim l_{\text{max}}\) 列中选,且 \(1\sim l_{\text{min}}\) 中不能全选。
- 全部删掉得到 \(a''\),给 \(f(a)\) 加上 \((-1)^{c-1} f(a'')\)。
下图是一次递归的例子:

考虑把轮廓转成 \(\texttt{01}\) 串,共有 \(n\) 个 \(\texttt{1}\),第 \(i-1\) 个 \(\texttt{1}\) 和第 \(i\) 个 \(\texttt{1}\) 之间有 \(l_i-l_{i-1}\) 个 \(\texttt{0}\)。
那么,一个 \(\texttt{01}\) 串的删除过程如下:
- 前 \(k\) 次,每次删除一个末尾为 \(\texttt{1}\) 的子序列,要求子序列中最左的 \(\texttt{1}\) 左边至少存在一个 \(\texttt{0}\) 未选入子序列。
- 第 \(k+1\) 次,删除剩余的整个串。
考虑给 \(\texttt{01}\) 串的每个位置标上它是第几次被删除的。那么有如下限制:
-
对于每个 \(1\le i\le k\),存在恰好一个 \(\texttt{1}\) 标了 \(i\) 且它的右边的每个位置标的都不是 \(i\)。
-
对于每个 \(\le k\) 的 \(\texttt{1}\),在它左边一定存在某个 \(\texttt{0}\) 标的数大于它。
考虑从左往右 DP。设 \(f_{i,j}\) 表示标了 \(\texttt{01}\) 串的前 \(i\) 个位置,共有 \(j\) 个数满足 \(\le i\) 的位置中存在某个 \(\texttt{0}\) 标的数大于它,且标这个数的最后一个 \(\texttt{1}\) 的位置 \(>i\)。
碰到一个 \(\texttt{0}\) 时,可以给它标这 \(j\) 个数之一(使 \(j\) 不变),也可以让它成为前缀非严格最大值(使 \(j\) 增加一个非负整数)。碰到一个 \(\texttt{1}\) 时,可以标这 \(j\) 个数之一(使 \(j\) 减少 \(0\) 或 \(1\)),也可以标 \(k+1\)(使 \(j\) 不变)。转移需要带上容斥系数。